差分隐私学习二

概要：

差分隐私，一种新型的隐私保护机制，主要针对：

• 如何在分享数据时定义隐私
• 如何在保证可用性的数据发布时，提供隐私保护的问题

以上两个问题提出了一个隐私保护的数据模型。

在差分隐私中，要求攻击者无法根据发布后的结果推测哪一条结果对应于哪一个数据集。该模型通过加入随机噪声的方法来确保公开的输出结果不会因为一个个体是否在数据集中而产生明显的变化，并对隐私泄露程度给出了定量化的模型。

因为一个个体的变化不会对数据查询结果有显著的影响，所以攻击者无法以明显的优势通过公开发布的结果推断出个体样本的隐私信息。

差分隐私基础

差分隐私并不是要求保证数据集的整体性的隐私，而是对数据集中的每个个体的隐私提供保护。

使攻击者在观察查询结果后无法推断是哪个个体在数据集中的影响，使查询返回这样的结果，因此也就无法推断有关个体隐私的信息。换言之，攻击者无法得知某个个体是否存在于这样的一个数据集中。

定义：

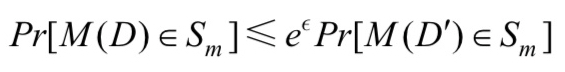
M: 一个随机算法
Pm: 为算法M可以输出的所以值的集合
D、D': 任意的一对相邻数据集
Sm: Pm的任意子集
ε：隐私保护预算  艾普西龙
算法 M 满足以上公式时，则称算法M满足 ε-差分隐私

参数ε越小

• 作用在一对相邻数据集上的差分隐私算法返回的查询结果的概率分布越相似。
• 攻击者越难区分这一对相邻数据集。
• 保护程度越高
• 当ε=0时，攻击者无法区分这一对相邻数据集，保护程度最高。

ε越大，保护程度越低。

差分隐私机制将一个正常的查询函数 f () 的查询结果, 映射到一个随机化的值域上, 并以一定的概率分布来给用户返回一个查询结果。通过参数 ε 来控制一对相邻数据集上的概率分布的接近程度, 达到在一对相邻数据集上, 输出结果几乎一致的目的。从而使得攻击者无法区分这一对相邻数据集, 实现保护数据集中个体隐私信息的目的。

差分隐私四性质：

• 顺序合成

  对于任意k个算法，分别满足： ε1-差分隐私， ε2-差分隐私，...， εk-差分隐私，将他们作用于同一个数据集上时，满足 （1-k）∑ε => (ε1+ε2+ε3+...+εk)-差分隐私
  

  这个性质说明了：当有一个算法序列同时作用于同一个数据集上时，最终的差分隐私预算 ε 等价于算法序列中所有算法的 ε 的和。

• 平行合成

  把一个数据集 D 分成 k 个集合，分别为 D1,D2,...,Dk，令A1,A2,...,Ak是k个分别满足 ε1，ε2，...，εk的差分隐私算法，则 A1(D1),A2(D2),...,Ak(Dk)的结果满足 max(ε1,ε2,ε3...εk)
  

  这个性质说明了：当有多个算法序列分别作用在一个数据集上多个不同子集上时，最终的差分隐私预算加价于算法序列中所有算法预算的最大值。

• 变换不变性

  给定任意一个算法 A1 满足 ε-差分隐私，对于任意算法 A2 (A2不一定是满足差分隐私的算法)，择优 A(D) = A2(A1(D)) 满足 ε-差分隐私。
  

  这个性质说明了：差分隐私对于后处理算法具有免疫性，如果一个算法的结果满足 ε-差分隐私，那么在这个结果上进行的任何处理都不会对隐私保护有所影响。

• 中凸性

  给定2个算法 A1 和 A2 满足 ε-差分隐私，对于任意的概率 p ∈ [0,1]，用符号 Ap 表示为一种机制，它以 p 的概率使用 A1 算法，以 1-p 的概率使用 A2 算法，则 Ap 机制满足 ε-差分隐私 。
  

  这个性质说明了：如果有两个不同的差分隐私算法，都提供了足够的不确定性来保护隐私，那么可以通过选择任意的算法来应用到数据上，实现对数据的隐私保护。只要选择的算法和数据是独立的。

顺序合成、平行合成可以被用来控制一个差分隐私机制在使用中所需要的隐私预算。

控制隐私预算的目的：如果在一个较低隐私预算参数 ε 的情况下，攻击者对一个数据集进行了多次查询，那个根据性质 顺序合成，攻击者实际上获得了多次查询的隐私预算的和，这就破坏了原本设定的隐私预算。所以需要控制隐私预算的上限，来通过上述的性质来计算合适的隐私预算上限。

差分隐私模型

差分隐私可以通过在查询结果上加入 噪声 来实现对用户隐私信息的保护，噪声量的大小是一个关键的量：

• 要使加入的噪声既能保护用户隐私
• 又不能使数据因为加入过多的噪声，导致数据不可用

函数敏感度，是控制噪声的重要参数。通过全局敏感度来控制生成的噪声大小，可以实现满足差分隐私要求的隐私保护机制。差分隐私保护可以通过在查询函数的返回值中加入噪声来实现，但是噪声的大小同样会影响数据的安全性和可用性。通常使用敏感性作为噪声量大小的参数，表示删除数据集中某一记录对查询结果造成的影响。

全局敏感度

定义：对于一个查询函数f，它的形式为 f:D->R，其中D为一数据集，R是查询函数的返回结果。
在一对任意的相邻数据集 D 和 D' 上，它的全局敏感度定义如下：


|| f(D) - f(D') || 是 f(D) 与 f(D') 之间的曼哈顿举距离。

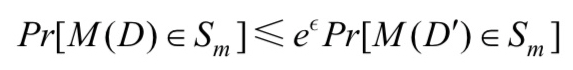
曼哈顿距离：两点在南北方向上的距离加上在东西方向上的距离，即d(i,j)=|xi-xj|+|yi-yj|

全局敏感度反映了一个查询函数在一对相邻数据集上进行查询时变化的最大范围，与数据集无关，只由查询函数本身决定。

敏感度是衡量一个函数的指标。对于一个函数𝑓:𝐷→𝑅𝑑f:D→Rd，其中D是数据库，函数在数据库上面进行查询，返回一个d维矢量，L1敏感度定义如下：

𝑆(𝑓)=max𝐷1,𝐷2‖𝑓(𝐷1)–𝑓(𝐷2)‖1S(f)=maxD1,D2‖f(D1)–f(D2)‖1

当函数f返回的结果是一个数字的时候，即𝑓:𝐷→𝑅f:D→R，那么L1敏感度为：

𝑆(𝑓)=max𝐷1,𝐷2|𝑓(𝐷1)–𝑓(𝐷2)|S(f)=maxD1,D2|f(D1)–f(D2)|

比如查询函数：满足特定条件下的记录有多少条。那么这个函数返回的结果是一个数字，它的敏感度𝑆(𝑓)≤1S(f)≤1，即：当查询结果当中没有一条满足的时候，查询的敏感度为0，当有一条或者多条满足的时候，敏感度为1。

拉普拉斯机制：一种简单、广泛用于数值型查询的隐私保护机制，对于数值型的查询结果，拉普拉斯机制在查询结果上加入一个满足 Lap(0, ∆ƒ/ε) 分布的噪音，返回加入噪音的结果。

R(D) = f(D) + x
f:为查询函数
x:满足拉普拉斯分布是噪声 

要求：所加入的拉普拉斯噪声的均值为0，这样输出的 R(D) 才是 f(D) 的无偏估计。

指数机制：

指数机制的意义在于防止了攻击者对数据集中 个体的投票情况的推测。例如在一次投票活动中, 一 共有3个候选人(用编号1到3表示), 10位选民, 攻击 者控制了除了选民 A 以外的其他 9 个选民(B, C, ..., J), 现在他的目的是推断选民 A 的投票情况。假设在 A 没有投票时, 每个候选人的得票数都为 3, 也就是说 B, C, ..., J 分别给每个候选人各投了一票, 那么如果 攻击者想要推断A的投票情况, 就可以通过最终的选 举结果看哪位候选人胜出来判断 A 的投票结果。但是, 如果加入指数机制, 就可以抵御这种攻击。