BUAA-OO-第三单元总结
北航计算机学院面向对象第三单元总结
由于本单元三次作业非常相似,都是基于上一次的功能和指令进行迭代扩展,因此以下总结都以第三次作业为例。
一、 利用JML规格生成数据并测试
本单元作业是契约式编程,不需要在架构设计上花太多心思,作业中容易出现Bug的情况是对官方给定的JML理解有误,以及设计的算法时间复杂度过高。因此本单元的自动测试基本是为了验证程序的功能正确性,而压力测试主要靠针对实现代码使用的算法手动构造数据,比如对并查集、最短路径的压力测试等。生成数据后的自动测试比较简单,与第二单元的多线程并行不同,本单元程序的运行结果是固定、可预测的,因此只需要找几个小伙伴对拍、逐行对比输出即可。(但要小心大家是不是同一个Bug
生成的数据分别对Message的相关操作、其余的操作进行测试,主要是因为Message的相关操作相对于其余的操作而言,结构和功能上都相对独立一些。
对Message的测试数据
# 首先初始化图以及表情列表 # add person for i in range(30): instrlist += "ap" …… # add relation for i in range(300): instrlist += "ar" …… # 增加两个组 instrlist += "ag" …… for i in range(25): # 25个人在组里,5个人不在组里以验证异常 instrlist += "atg" …… for i in range(15): # 初始15个表请 instrlist += "sei " …… # 对Message的相关指令进行随机性功能检测 for i in range(950): instr = random() if instr < 0.4 and len(msgId) != 0: instrlist += choice(["sm","sim"]) …… elif instr < 0.8: cnt += 1 if cnt == 5: # 每五个人增加一个msgId缺失,保证对异常抛出的检测 msgId.append(randint(1001, 5000)) cnt = 0 type = randint(0, 1) instrlist += choice(['arem','am','anm','aem']) …… elif instr<0.9: instrlist += "qm" …… elif instr<0.95: instrlist += "qp " …… elif instr < 0.97: instrlist += "qrm " …… elif instr<0.98: instrlist+="dce " …… else: instrlist += "cn" ……
对其余操作的测试数据
除开Message以外指令关联性较强,因此选择在同一张图上进行随机测试
# 初始化图 for i in range(people_num): instrlist += "ap" …… for i in range(group_num): instrlist += "ag" …… # 随机枚举指令,进行数据生成 for i in range(LENGTH - people_num): instr = choice(instrs) …… if instr == "qci": qci_num += 1 if instr == "qlc": qlc_num += 1 if instr == 'ar': Instrlist += ' ' …… elif instr == 'atg' or instr == 'dfg': …… elif instr == 'qv' or instr == 'qci': …… ……
而针对时间的压力测试,本单元只针对qbs指令(是否使用并查集、并查集是否路径压缩),qlc指令(是否对最小生成树朴素算法进行优化)构造了零图和完全图。(第三次互测摸了
二、 架构设计及维护策略
UML类图
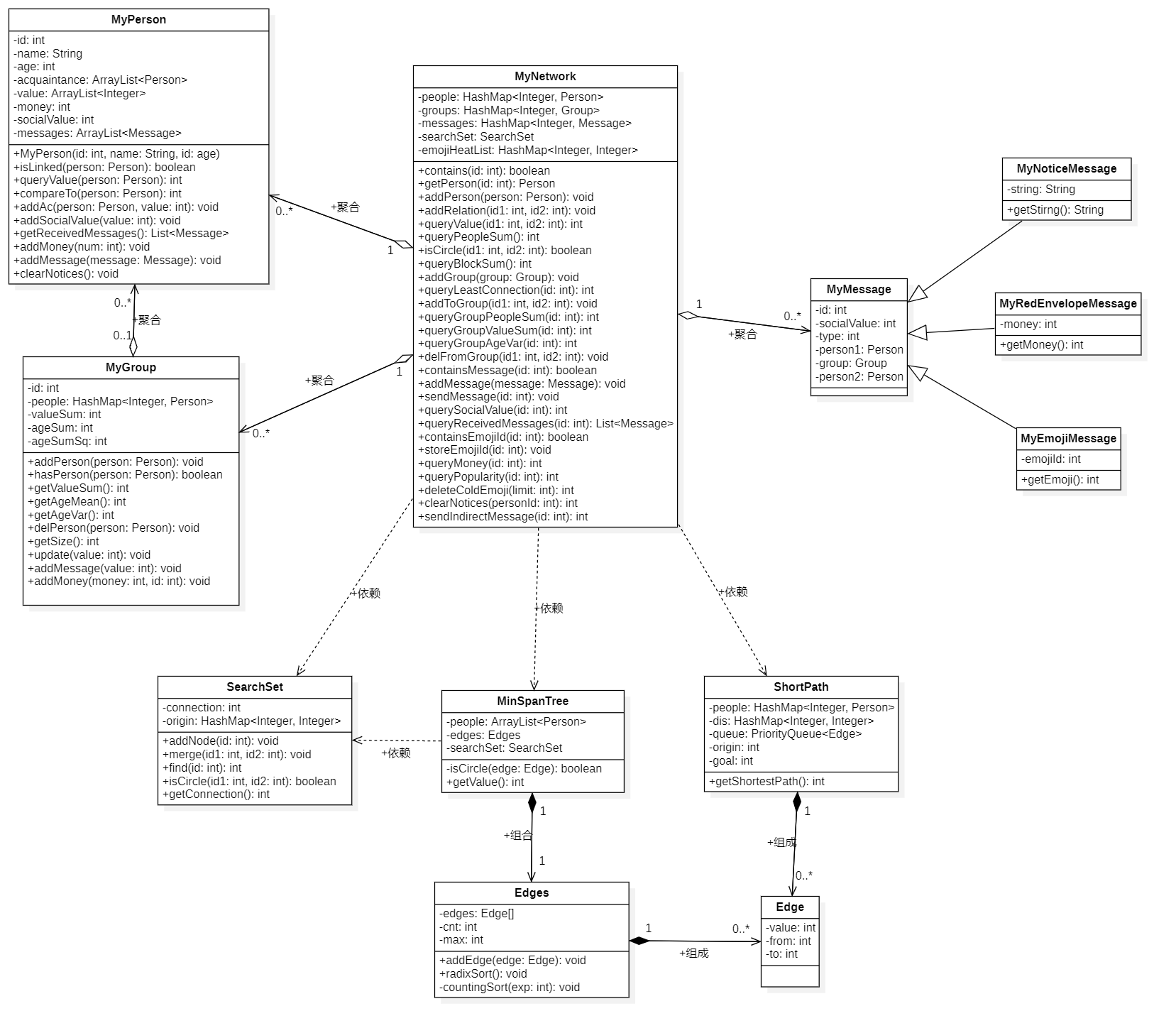
考虑到简洁性,上述UML类图没有包含异常类
架构设计
本单元的架构以及图的模型,基本上由官方包搭建好了,只要阅读并正确理解JML描述,大家的架构应该相差不大。阅读官方包不难发现,本单元作业主要是维护一个社交网络,以Person为图的节点,以Relation为图的无向边。针对这个图进行诸如:查询连通、最小生成树、最短路径等一系列操作。而我们要重点关注的,应该是使用怎样的数据结构、算法、容器来对图的一些属性进行维护,以便能够简洁、迅速地完成指令对图的修改和查询。
维护策略
路径压缩的并查集
通过阅读JML规格,不难发现本单元作业中的qci指令即为查询图中两点是否连通,qbs指令为查询图中连通分支数量,qlc指令为查询包含某点的最小生成树。这三个查询都能够借助并查集实现。相信并查集的相关实现大家都不陌生,在本单元作业中具体而言就是,在add person时向并查集中添加节点并将其设为一个源点(也就是它所在集合里的boss),在add relation时检查是否需要合并两个集合,更新源点。使用路径压缩的写法能够防止图退化成一条链时,多次查询首尾两个点连通关系可能会导致超时。同时以下给出的写法采用的是非递归的形式,这能避免上面描述的链结构时可能出现的爆栈情况。
public int find(int x) { int cur; int tmp; int root; root = x; while (root != origin.get(root)) { root = origin.get(root);//查找根节点 } cur = x; while (cur != root) //非递归路径压缩操作 { tmp = origin.get(cur); //用tmp暂存parent[cur]的父节点 origin.replace(cur,root); //parent[x]指向根节点 cur = tmp; //cur指向父节点 } return root; //返回根节点的值 }
基于基数排序优化的克鲁斯卡尔算法
第二次作业中的qlc指令实际上是查询包含某节点的最小生成树,最小生成树算法一般为prim和kruskal算法,但两算法算法的朴素算法时间复杂度都是O(n²)/O(e²),在本次作业中1e4量级的数据会超时。考虑到作业中稀疏图出现的概率应该是大于稠密图的,因此最终选择使用了kruskal算法。而针对该算法的优化就是对遍历的边按权值进行排序。其实使用堆排序优化就可以,java还有现成的优先队列用,但自己想尝试写写看基数排序效果怎么样,结果发现不如同学的堆排序(小丑竟是我自己。
具体写法其实和朴素算法几乎一样,不同的是需要在遍历前对边进行排序,而找边就不需要每次通过遍历寻找最小边,直接从当前索引下标开始,寻找能连通两个非连通分支的边即可。
public int getValue() { // 获取连通分支中的所有无向边 for (Person person1:people) { ...... ArrayList<Person> persons = ((MyPerson) person1).getAcquaintance(); for (int i = 0;i < persons.size();i++) { ...... edges.addEdge(new Edge(value.get(i),id1,id2)); } }
// 对边进行升序排序 edges.radixSort(); ...... while (cnt < sum && index < sumOfEdge) { Edge edge = edges.getEdge(index); // 选择能将两个非连通分支连通的最短边 while (isCircle(edge)) { index++; edge = edges.getEdge(index); } rst += edge.getValue(); ...... //更新并查集
searchSet.merge(searchSet.find(edge.getFrom()),searchSet.find(edge.getTo())); ...... } return rst; }
堆优化的迪杰斯特拉算法
第三次作业中的sim指令实际上是查询两个连通点之间的最短路径,最短路径的算法有弗洛伊德算法(时间复杂度O(n³),pass),迪杰斯特拉算法(朴素写法时间复杂度O(n²),pass;堆优化后O((m+n)logn),可以考虑)以及SPFA算法(平均O(m),最坏O(mn)),由于对于网络流的算法不是很熟悉,同时在网上查阅资料发现有很多前辈指出SPFA算法的时间复杂度很玄学,因此最后选择使用了堆优化的迪杰斯特拉算法。
三、 分析代码中的性能问题
比较容易发现的性能问题在维护策略中已经给出,但除此之外这次作业中还有不少可能因为性能问题而超时的地方。
说到底JML仅仅是通过规格化的语言描述了方法和类的功能、执行条件、过程。规格化语言是死板的,但写程序的人是灵活的,单纯依照JML的描述编写的代码很有可能是性能最差的(尤其是比较复杂的方法,涉及到多重循环时)。在阅读JML编写程序时,不应该不加以思考,盲目地跟从JML的描述coding,而是要充分理解其描述的功能,思考某些循环是否真的有必要?某些嵌套循环是否能通过别的方法去掉?笔者认为只要在编写过程中对每个描述持有怀疑态度,就基本不会出现性能问题。
除开维护策略中提到的以外,JML给出的写法可以优化的地方大概有以下几点:
- 善用容器
本单元作业出现的各个类的对象都有其唯一的id,善用HashMap、HashSet等容器,可以去除JML中出现的很多循环。比如Group类中的hasPerson()方法,JML描述为
ensures \result == (\exists int i; 0 <= i && i < people.length; people[i].equals(person));
看起来是一个O(n)的方法,实际上使用HashMap作为存储Person的容器,利用HashMap.containsKey()方法,就能优化至O(1)的复杂度。诸如此类的优化本单元作业里还有很多,这里就不再赘述。
- 小心嵌套调用
有的函数从表面上看只是O(n)的时间复杂度,然后其中却暗藏杀机,它在每次循环的时候调用了某个方法,而当该方法也是0(n)的复杂度时,实际上最后运行下来就会是O(n²)的复杂度,存在TLE的风险。比如Group类中的getAgeVar()方法,JML描述为
ensures \result == (people.length == 0? 0 : ((\sum int i; 0 <= i && i < people.length;(people[i].getAge() - getAgeMean()) * (people[i].getAge() - getAgeMean())) / people.length));
这个描述看上去时间复杂度只有O(n),但它每次循环都调用了getAgeMean()方法,该方法的JL描述同样为O(n)的时间复杂度,这样嵌套调用最终就导致了getAgeVar()方法的复杂度变成了O(n²)。实际上第二次作业互测同组就有同学对于qgvs指令没有考虑函数嵌套调用出现了tle。
四、 Network扩展
任务分析
- 对于Advertiser、Producer、Customer可以分别继承抽象类Person,共有id、money等属性,sendMessage()等方法。
- 对于消费者,可以添加一个commodityType[] commodityPrefer属性记录偏好,可根据偏好搜索商品。
- 对于Advertiser,可以使用单例的模式,将其视为一个“平台”会更加方便。
- 对于advertise、produce、purchase可以分别继承类Message,将这三个行为视为一个Person对象发送的信息。
方法JML
sendAdvertisement()
/*@ public normal_behavior @ requires containsMessage(id) && (getMessage(id) instanceof Advertisement); @ assignable messages; @ assignable people[*].messages; @ ensures !containsMessage(id) && messages.length == \old(messages.length) - 1 && @ (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id; @ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i])))); @ ensures (\forall int i; 0 <= i && i < people.length; person[i].likeType(\old(((Advertisement)getMessage(id))).getType) ==> @ ((\forall int j; 0 <= j && j < \old(person[i].getMessages().size()); @ person[i].getMessages().get(j+1) == \old(person[i].getMessages().get(j))) && @ (person[i].getMessages().get(0).equals(\old(getMessage(id)))) && @ (person[i].getMessages().size() == \old(person[i].getMessages().size()) + 1))); @ also @ public exceptional_behavior @ signals (MessageIdNotFoundException e) !containsMessage(id); @ signals (MessageNotAdverException e) containsMessage(id) && !(getMessage(id) instanceof Advertisement); @*/ public void sendAdvertisement(int id) throws MessageIdNotFoundException, MessageNotAdverException;
sendPurchase()
/*@ public normal_behavior @ requires containsMessage(id) && (getMessage(id) instanceof Purchase); @ requires (getMessage(id).getPerson1() instanceof Customer) && (getMessage(id).getPerson2() instanceof Producer); @ assignable messages; @ assignable getMessage(id).getPerson1().money; @ assignable getMessage(id).getPerson2().messages, getMessage(id).getPerson2().money; @ ensures !containsMessage(id) && messages.length == \old(messages.length) - 1 && @ (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id; @ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i])))); @ ensures (\old(getMessage(id)).getPerson1().getMoney() == @ \old(getMessage(id).getPerson1().getMoney()) - ((Purchase)\old(getMessage(id))).getMoney() && @ \old(getMessage(id)).getPerson2().getMoney() == @ \old(getMessage(id).getPerson2().getMoney()) + ((Purchase)\old(getMessage(id))).getMoney()); @ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2().getMessages().size()); @ \old(getMessage(id)).getPerson2().getMessages().get(i+1) == \old(getMessage(id).getPerson2().getMessages().get(i))); @ ensures \old(getMessage(id)).getPerson2().getMessages().get(0).equals(\old(getMessage(id))); @ ensures \old(getMessage(id)).getPerson2().getMessages().size() == \old(getMessage(id).getPerson2().getMessages().size()) + 1; @ ensures getProduct(\old((Purchase)getMessage(id)).getProductId()).getNum() == \old(getProduct(\old((Purchase)getMessage(id)).getProductId()).getNum()) + 1; @ also @ public exceptional_behavior @ signals (MessageIdNotFoundException e) !containsMessage(id); @ signals (MessageNotPurchaseException e) containsMessage(id) && !(getMessage(id) instanceof Purchase); @ signals (PersonNotCustomerException e) containsMessage(id) && (getMessage(id) instanceof Purchase) && @ !(getMessage(id).getPerson1() instanceof Customer); @ signals (PersonNotAdvertiserException e) containsMessage(id) && (getMessage(id) instanceof Purchase) && @ (getMessage(id).getPerson1() instanceof Customer) && !(getMessage(id).getPerson2() instanceof Producer); @*/ public void sendPurchase(int id) throws MessageIdNotFoundException, MessageNotPurchaseException, PersonNotCustomerException, PersonNotAdvertiserException;
querySale()
/*@ public normal_behavior @ requires containsProduct(id); @ ensures \result == getProduct(id).getNum(); @ also @ public exceptional_behavior @ signals (ProductIdNotFoundException e) !containsProduct(id); @*/ public /*@ pure @*/ int querySale(int id) throws ProductIdNotFoundException;
五、 学习体会
- 切实体会到JML语言的严谨性带来的力量,能够零歧义地描述一个模块的功能和运行流程,我认为是一个很了不起的作品。
- 同时JML语言一定程度上也存在局限性和缺点,在面对较为复杂的方法时,JML的阅读和书写都会变得非常复杂。以qlc方法为例,刚开始写第二次作业时没有注意到指导书上提示的“最小生成树”算法,初见qlc方法的JML描述不得不让我望而生畏。层层剖析它的括号,用纸笔一点点推导,二十多分钟后才终于恍然大悟,这xx不就是最小生成树吗?如果用数学语言甚至一行公式就能描述清楚。。。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号