BUAA-OO-第一单元总结

BUAA-OO-第一单元总结

全文目录

• 一、基于度量分析程序结构和架构设计
• 第一次作业
• 第二次作业
• 第三次作业
• 二、分析自己程序的bug
• 三、hack策略以及发现的问题
• 四、感悟和心得体会

一、基于度量分析程序结构和架构设计

第一次作业

第一次作业难点在于对表达式的解析，由于表达式的构成层次存在嵌套关系，初次接触时显得有些无从入手，需要花大量时间理清作业的形式化表述，并考虑好需要创建哪些类，类和类之间存在哪些关系，如何对表达式进行解析。由于本次作业仅含有x一个自变量，也只有幂函数一种初等函数，在理清表达式构成因子的逻辑关系后，表达式的化简反而并不难处理，只需要选择好容器和变量类型即可。

参考助教的表达式解析方法，并根据根据形式化表述中的描述：

因子 → 变量因子 | 常数因子 | 表达式因子

故可以提供一个Factor接口，创建Expression类（即表达式因子）和Number类（即变量因子和常数因子）两个类实现该接口，同时创建一个Term类作为Expression类的组成。其中Expression由Term构成，在程序中表现为Expression中有一个类型为ArrayList<Term>的属性；Term由Factor构成，在程序中表现为Term类有一个类型为ArrayList<Factor>的属性。通过这种方式解析，即将原式划分为表达式、项、幂函数三个层次。

而对于计算来说，一般性的思路为：对表达式各项进行计算并合并，再对表达式进行合并同类项，具体流程如下图所示

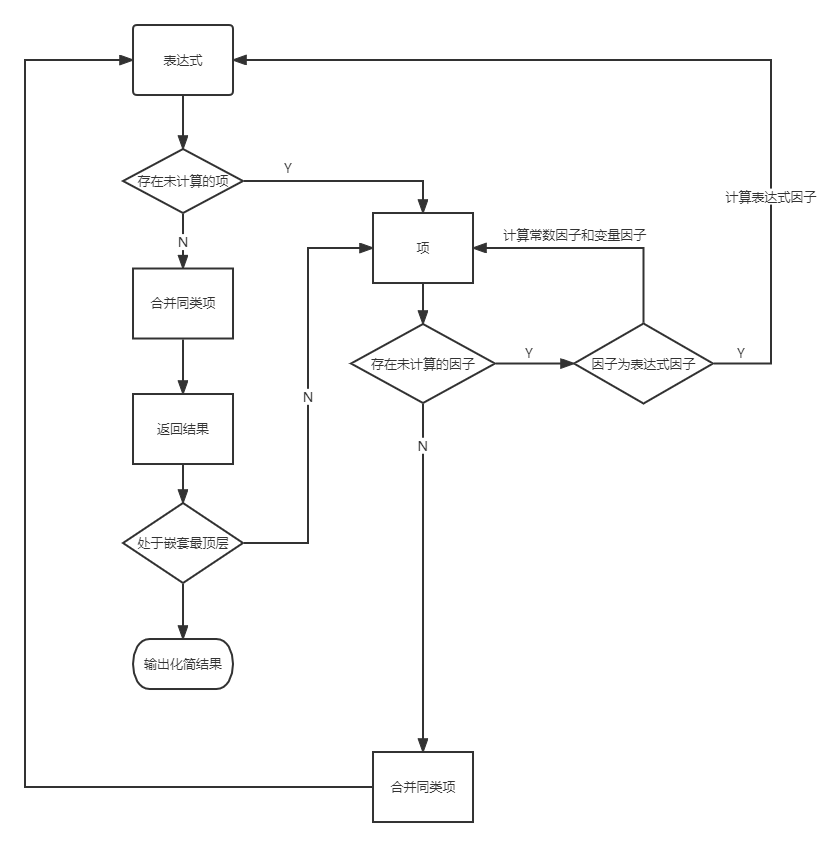
同时由于第一次作业中仅存在自变量x，并且仅存在幂函数一种初等函数，于是笔者通过HashMap存储最终化简结果，其中Key为幂函数的次数，Value为幂函数的系数。通过检索HashMap的键值即可进行同类项合并以及最终的表达式输出。

在设计中遇到连续符号的处理问题，因为不想给表达式因子赋予指数和系数两个属性（事实上解析时对表达式的乘方笔者是通过乘多个相同因子处理的），而且因为没有充分理解形式化表述中符号的要求，所以一度成为笔者设计时的一个难点。最后采用了如下方法，解析遇到符号时进行循环处理，如果符号后面紧跟表达式，则视为表达式乘了一个1或-1。

第一次作业的UML图如下所示，整体来看本次作业实现方式还是比较“面向对象”的，对表达式的层次分析逻辑合理、思路清晰，并且具有较强的鲁棒性，强测和互测都没出现问题，在测试时也只发现一处解析时对括号的匹配存在错误。但如print()等部分方法，还是存在“面前过程”的现象，后续可以通过在Term类和Number类同样提供一个print()方法解决，调用Expression类的print()方法的过程中调用Term类的print()方法，以此来减少Expression承担的非必要责任和功能。

 

 

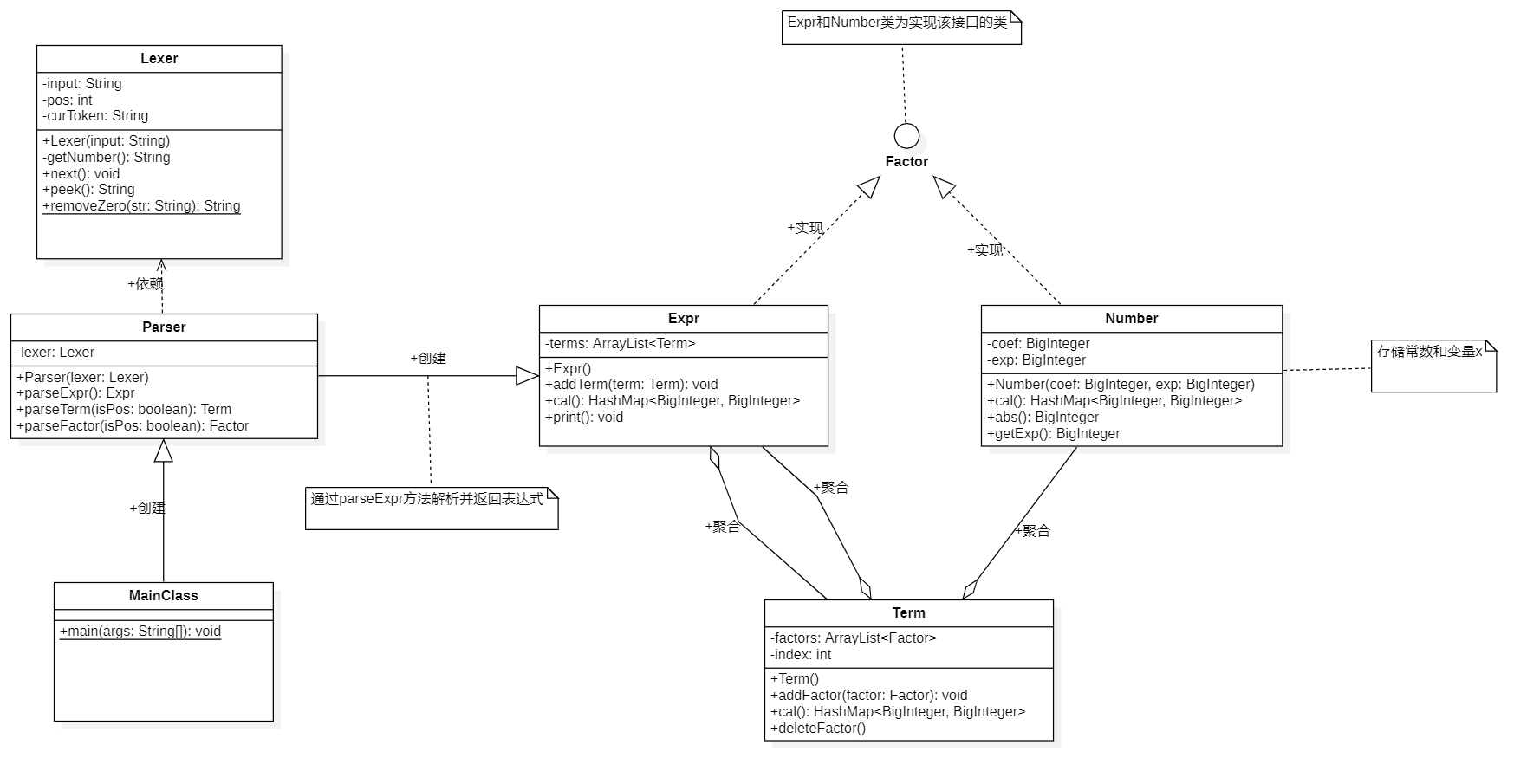
第一次作业复杂度分析：

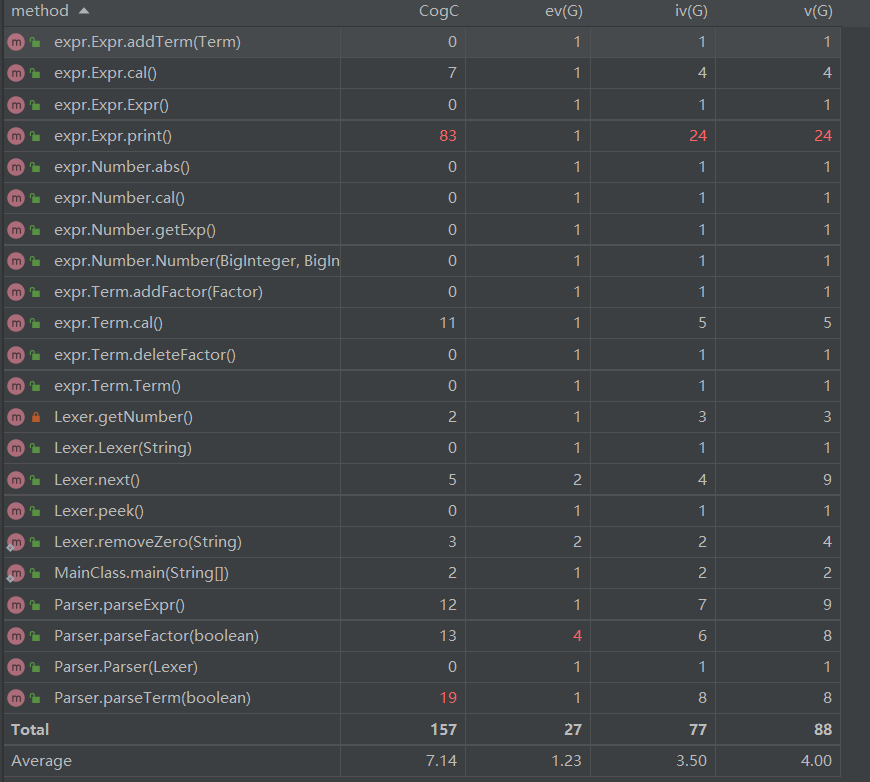
由于Expr.print()方法基本采用“面向过程”的思路编写，导致代码量长，同时方法复杂度也比较高。其次是Parser类中的各方法，由于解析过程情况比较复杂，也导致方法复杂度较高。这与上述分析一致。

 

第一次作业代码量：

第二次作业

因为“解析表达式”这个boss在第一次作业中已经拿下了，显得第二次作业难度稍低于第一次作业。第二次作业需要新加入三角函数因子，以及函数和求和函数。对于三角函数，只需新建一个Trigo类并实现Factor接口即可。而处理函数和求和函数，主要分为了两个流派，一是将函数视为一种特殊的表达式因子，解析表达式时对其进行处理。另一种方法是在读取到字符串的时候，对字符串进行预处理，将函数表达式替换为普通表达式的形式。笔者采用了第二种方法，这种方法具有以下优点：

逻辑清晰，不破坏原程序的结构

处理方便，只需要进行简单的正则表达式匹配和字符串处理即可实现

将任务独立出来，尽可能做到“高内聚，低耦合”，并且也让debug的过程轻松一些

第二次作业UML图如下所示，相较于第一次作业而言新增的类并不多。新增了一个Func类储存读入的函数形式；一个PreProcess类对读入的表达式进行预处理，如去除空白字符，对函数和求和函数进行字符串替换；一个Trigo类存储三角函数因子。由于第一次所用计算方法比较巧妙迅速，但同时也存在着普适性较弱的问题，面对多变量的处理尚有一战之力，但再加入三角函数后就有点力不从心了。于是笔者对计算方法进行了重构，显得某些部分存在逻辑混乱的现象，也导致部分方法复杂度较高。

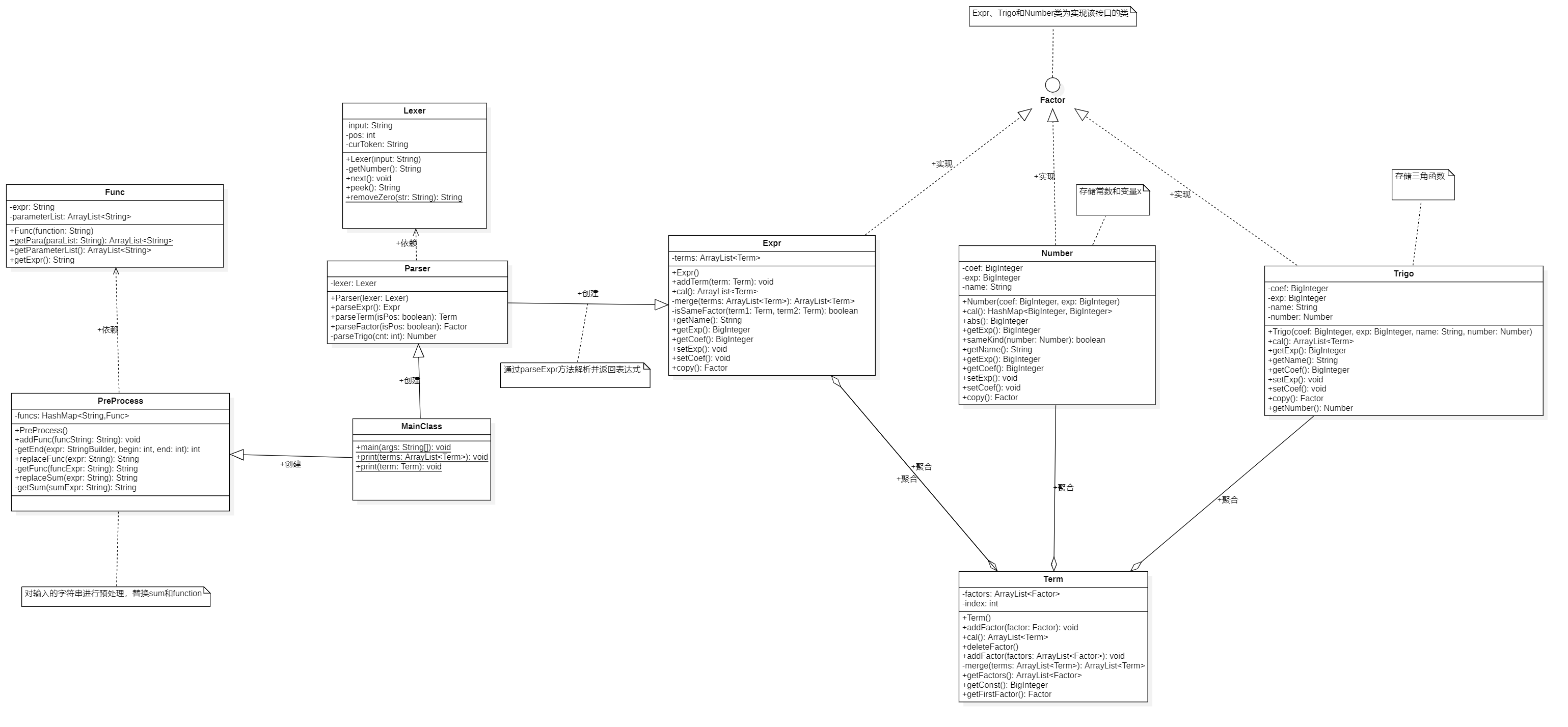
第二次作业复杂度分析：

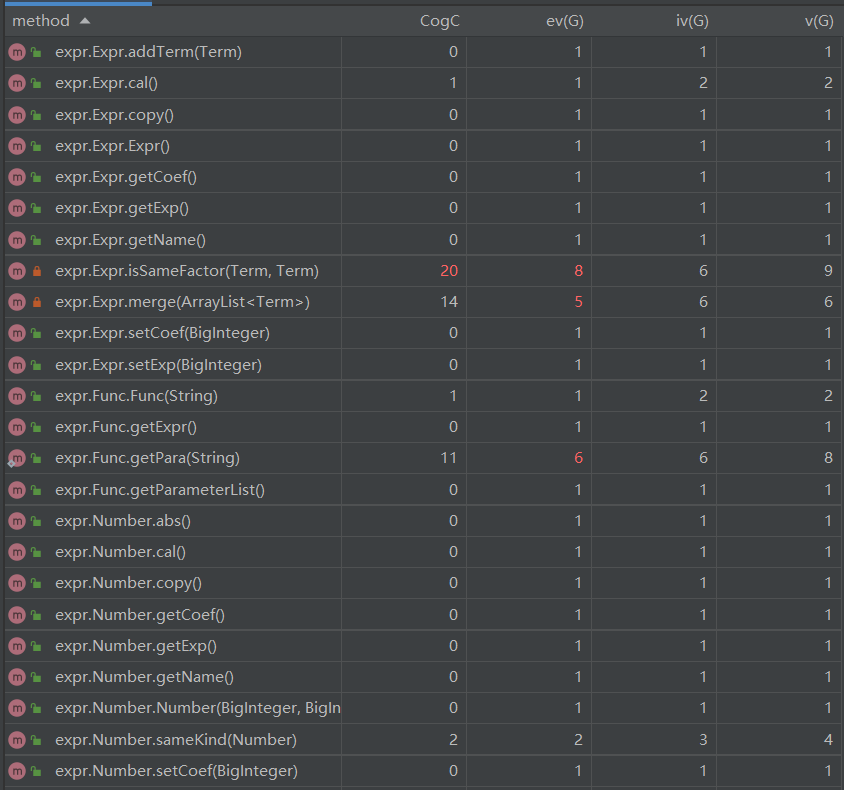
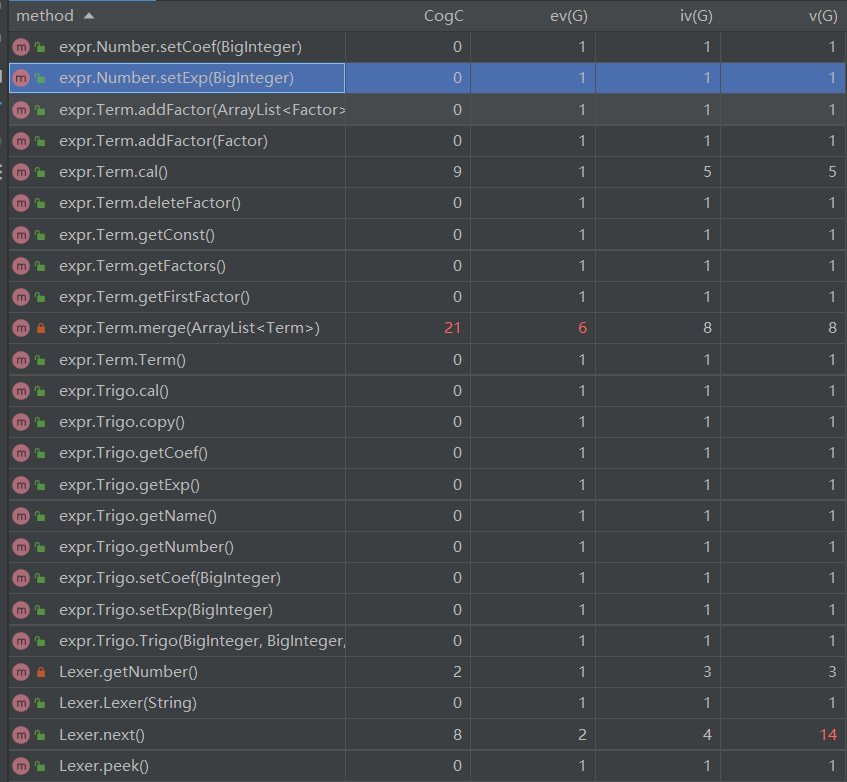
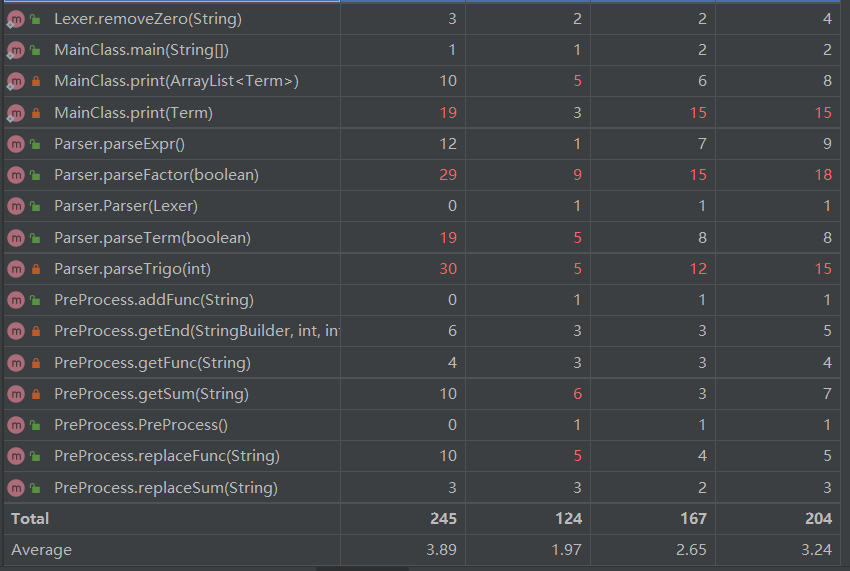
可以看到，由于对第一次作业中的print()方法用面向对象的思路进行改良，尽管第二次作业处理难度大于第一次作业，方法整体复杂度依然有所下降。

第二次作业代码量：

第三次作业

第三次作业应该是整体难度最低的一次，但笔者却问题频出，主要原因还是这次没有摆，对输出结果进行优化了。这次作业增加了函数嵌套和三角函数内部嵌套表达式因子，前者对于我的架构而言需要修改的地方很少，因为第一次作业中的解析时采用递归梯度下降的方法，这次作业的嵌套括号并没有什么问题，对于嵌套函数而言，也仅需要在预处理替换函数进行递归调用即可。主要难点还是在三角函数内部嵌套表达式因子上，需要修改三角函数的内部属性，以及一些用以比对两三角函数类型是否相等方法。

在对形如sin((x-sin(x)+cos(x**2))) + sin((-x+sin(x)-cos(x**2))) = 0的优化中 ，由于笔者并未使用Hash类的容器存储各个类的属性，在判断优化条件时需要消耗大量的时间对三角函数的内部表达式因子进行多次遍历，让本就跑得很慢的代码更是雪上加霜。于是在处理这个问题时，选择了模仿hash表的思想，依照所定规则赋予三角函数内每个项一个权值，根据权值判断此时的三角函数是否需要提出一个负号。但由于笔者所定规则没有经过足够的数据测试和数学证明，也没有考虑处理哈希冲突，这里就不放出来误导各位了。

第三次作业新增功能并不多，程序结构与第二次作业基本相同，仅更改了Trigo类属性的类型。大部分新增代码都是在对计算结果进行长度优化。

第三次作业复杂度分析：

 

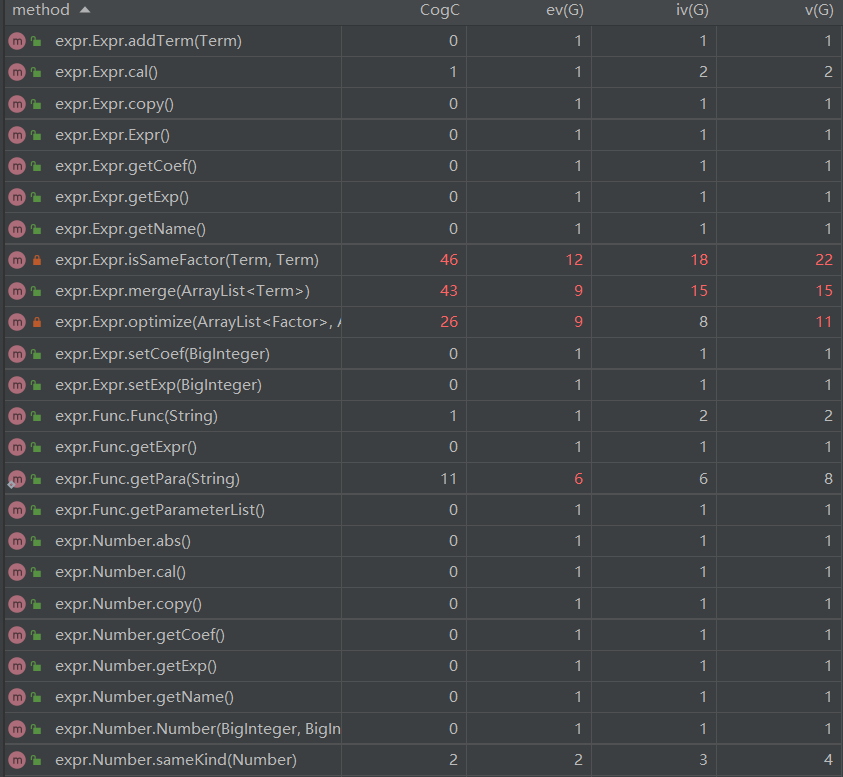
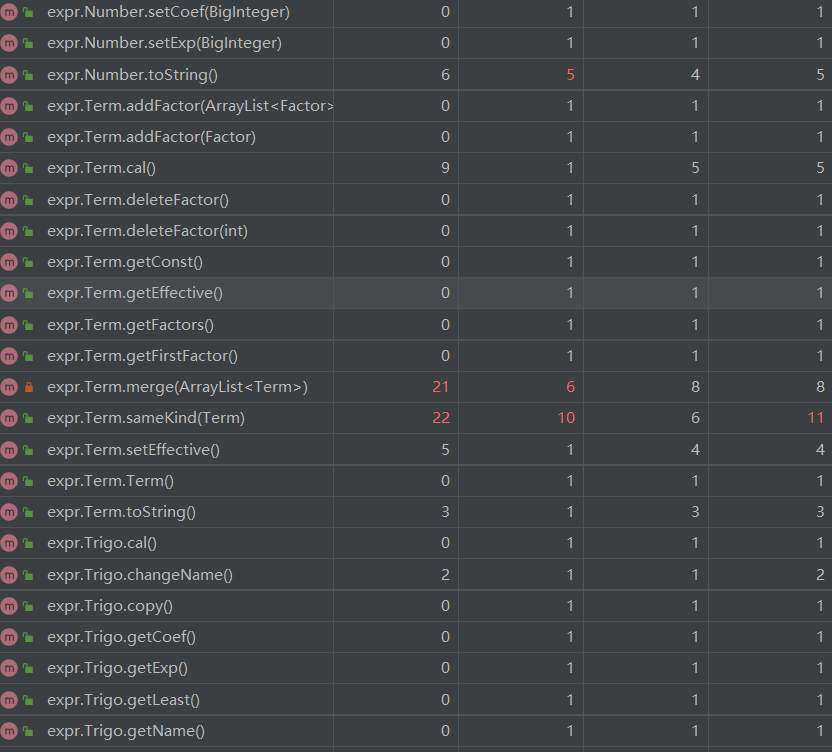
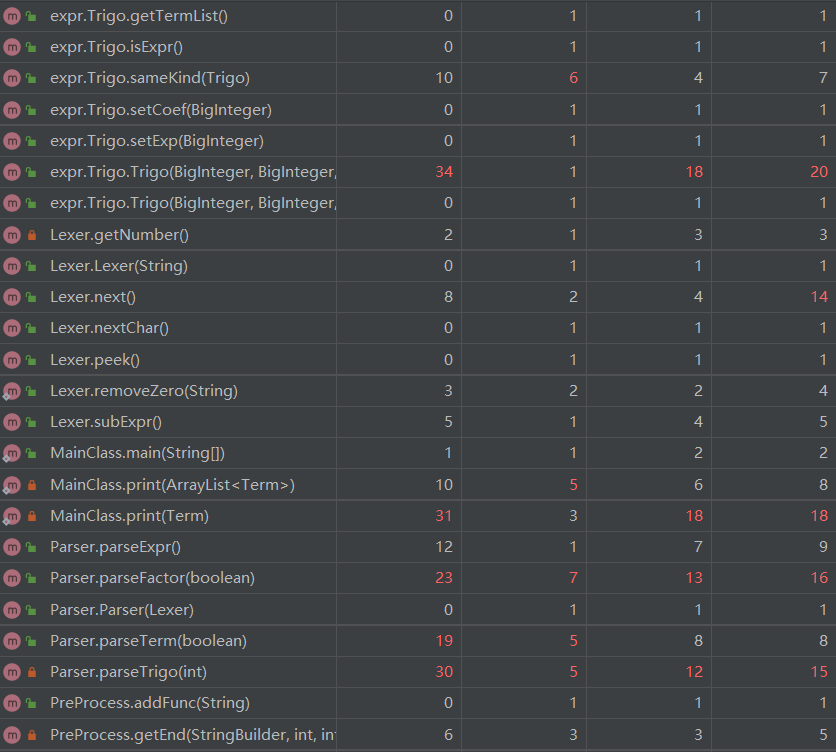
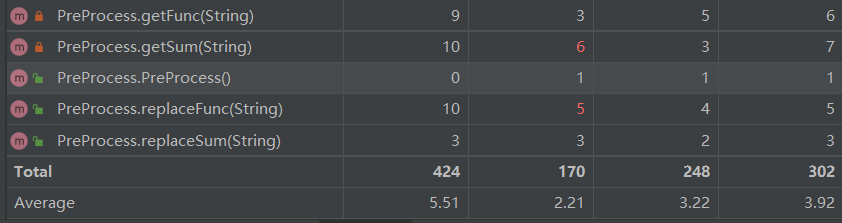
因为第三次作业新增了不少优化策略，并且三角函数的内部因子取消了对表达式的限制，所以部分方法的复杂度相较于的第二次作业提高不少，之后可以对复杂度过高的方法进行功能分割，将其分为多个方法，负责不同职能。

第三次作业代码量：

 

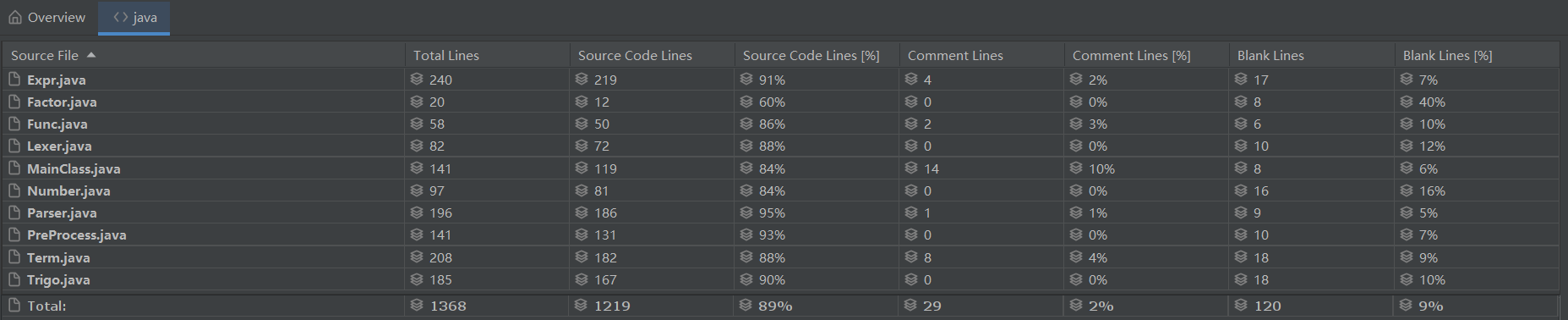
二、分析自己程序的BUG

因为程序结构比较清晰，并且提交前也做了很多测试，三次作业中只有第三次互测时被发现了Bug，原因在处理求和函数中涉及到i**2时，因为没考虑到数字也可以有次幂，没有对常数的次幂进行处理。

虽然公测和互测中没有发现太多bug，但自己测试的时候倒是发现了不少。

1. 由于第二次作业中三角函数的因子不可能存在三角函数，所以对三角函数判同类型时，没有对名字（即sin和cos）进行判断，导致程序会认为sin(sin(x)) 和 sin(cos(x))是同类型的三角函数。
2. 括号匹配问题。由于第三次作业涉及大量括号嵌套，包括三角因子的括号嵌套，自定函数的括号嵌套，尤其是因为采用字符串替换的方法处理自定函数，还会再引入大量括号，于是在解析三角函数的内部因子时发现了很多因括号匹配导致的bug。
3. 对象的浅拷贝问题。在合并同类项时，会涉及很多对对象属性的直接赋值操作，如果不小心使用了浅拷贝，会导致在操作某对象时，对另一个对象也进行了赋值。为了避免这种情况，笔者为每个因子设计了copy()方法，返回的是与当前对象属性完全相同的一个新创建的对象。但后面才知道可以重写clone()方法。

 

三、hack策略以及发现的问题

本单元进行hack时基本采用如下策略：

• 通读对方的代码，检查是否存在比较简单发现的、大家共有的一些问题，如项的系数、求和函数的上下界不使用BigInteger存会存在爆int的风险，sin(-x)提出负号时有没有归并到统一的系数上（部分同学存在sin(-x)**2 = -sin(x)**2的bug）等。
• 使用自己在测试时发现的干掉自己的数据进行hack尝试，这种方法在针对和自己架构相似的同学时效果很好。
• 利用自动生成的数据进行轰炸，进行尽可能完全的覆盖性测试。

不少同学都是在优化部分出现了bug，比如复杂情况下的cos(x)**2+sin(x)**2的优化，处理形如sin(x)**2*cos(x)**2+sin(x)**2*cos(x)**2的表达式时，有同学的优化方法在判定两项均有sin(x)**2后，仍然会将后项的cos(x)**2和前项的sin(x)**2进行匹配，认为符合cos(x)**2+sin(x)**2的条件。我认为代码量越大，就越容易产生问题，尤其是当优化情况多、优化条件比较复杂时，一定要多对优化部分进行分析与测试，以免因小失大。

但测试时我也发现有的大佬甚至进行了二倍角优化、诱导公式的优化，而且简单测试后也很难发现问题，在这里膜一波ORZ。

四、感悟与体会

本单元作业对于面向对象小白来说是一次难度极高的挑战，助教在实验训练中提供的递归梯度下降解析法示例，几乎成了我第一次作业的救星，提供了一个很棒的解析思路，在此特别感谢助教组和课程组的不杀之恩。

在各次作业的迭代中，由于在新增功能时没有考虑清楚前一次作业的已有功能是否满足需求，导致产生了不少问题。在后续单元的作业中，最好还是先画UML图构建好整个作业的架构，这样在后续的迭代中不至于发生遗忘前一次作业的细节的情况。同时，在第一次作业选择计算方法时，尽管考虑到后续可能会不限制自变量个数，但还是没有想到会引入三角函数，导致第一次作业的计算方法不再适用于后续作业（当然也可能是太菜了，没有想到解决办法），以后在设计时还是应该多结合后续迭代情况，避免连程序的基石都要重构的情况（真的不想重构辣）。

但人的预想和远见毕竟是有限的，在遇到当前架构确实无法处理的情况时，还是应当该下手时就下手，及时进行重构。第二次作业时正是因为犹豫不决，导致决定重构时已经是周三晚上了，显得时间非常紧，而且测试也不太够，所幸在强测和互测时没有暴露出问题。

希望之后的几个单元同学们能顺利通过~