2023省选武汉联测7

T1 动点 (point)

首先考虑两种操作，根据高中计算几何知识很容易得到这两种变换后点的坐标，首先考虑 \(1\) 操作，假设旋转中心 \(P\) 为原点，考虑将点 \(A(x_0,y_0)\) 绕点旋转 \(\alpha\) 到 \(B\) ，设 \(\overrightarrow{OA}\) 与 \(x\) 轴的夹角为 \(\beta\) ，如下图：

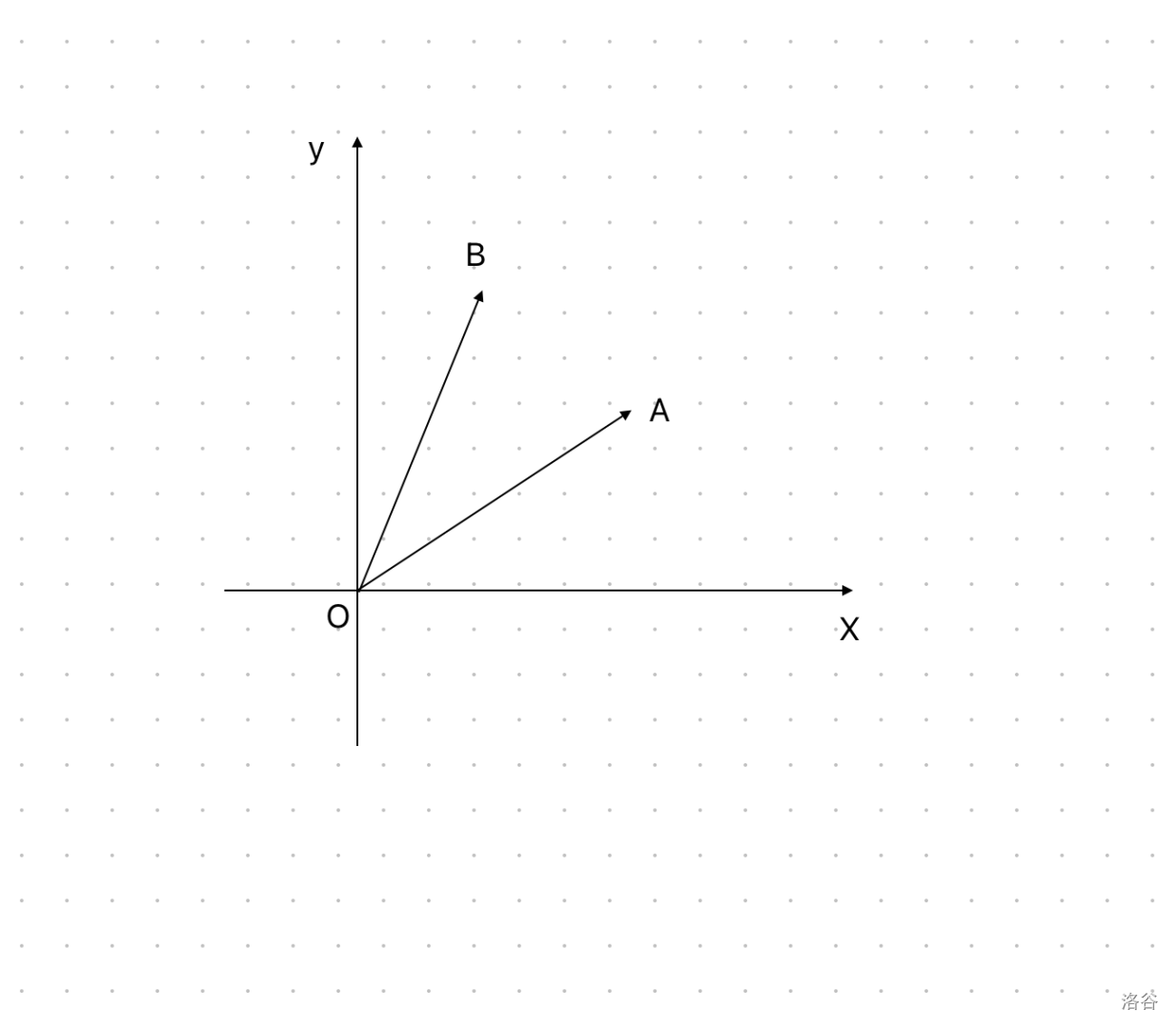
设 \(\mid\overrightarrow{OA}\mid=\mid\overrightarrow{OB}\mid=L\) ，比较显然 \(\overrightarrow{OA}=(\cos\beta L, \sin\beta L),\overrightarrow{OB}=(\cos(\alpha+\beta)L,\sin(\alpha+\beta)L)\) ，简单化简一下发现 \(\overrightarrow{OA}=(\cos\alpha x_0-\sin\alpha y_0,\sin\alpha x_0+\cos\alpha y_0)\) ，旋转中心不为原点的情况简单平移一下即可。

其次考虑操作二，设直线为 \(Ax+By+C=0\) ，直线的方向向量为 \(\vec{\alpha}\) ，设操作的点 \(P=(x_0,y_0)\) ，设操作后点移动到了 \(Q(x,y)\) ，容易发现其满足一下关系：

\[\begin{cases} Ax+By+C=0\\ \overrightarrow{PQ}\cdot\vec{\alpha}=0 \end{cases} \]

简单解方程可以得到：

\[\begin{cases} x=\tfrac{B^2x_0-ABy_0-AC}{A^2+B^2}\\ y=\tfrac{A^2y_0-ABx_0-BC}{A^2+B^2} \end{cases} \]

发现这两种操作都是线性变换，对于没有修改的操作可以直接用线段树维护矩阵乘，考虑加入修改，对于第一种操作，容易发现我们将操作点 \(P\) 向 \((-u,-v)\) 平移后进行操作，之后在平移回来，很容易用线段树维护，对于第二种操作，同样将操作点关于 \(Ax+By+C=0\) 对称，操作后在对称回去，需要注意的是，对称后原先的逆时针旋转变成了顺时针旋转，在线段树维护两个旋转方向的矩阵即可。

code

#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int max1 = 1e5;
const long double pi = acos(-1);
int n, m;
struct Option
    { int opt, A, B, C; } g[max1 + 5];
struct Matrix
{
    long double matrix[3][3];
    void Identity ()
    {
        for ( int i = 0; i < 3; i ++ )
            for ( int j = 0; j < 3; j ++ )
                matrix[i][j] = i == j;
        return;
    }
    Matrix operator * ( const Matrix &A ) const
    {
        Matrix res;
        for ( int i = 0; i < 3; i ++ )
        {
            for ( int j = 0; j < 3; j ++ )
            {
                res.matrix[i][j] = 0;
                for ( int k = 0; k < 3; k ++ )
                    res.matrix[i][j] += matrix[i][k] * A.matrix[k][j];
            }
        }
        return res;
    }
};
struct Segment_Tree
{
    #define lson(now) ( now << 1 )
    #define rson(now) ( now << 1 | 1 )
    struct Struct_Segment_Tree
        { Matrix sum1, sum2, lazyl, lazyr; bool rev; } tree[max1 * 4 + 5];
    void Push_Up ( int now )
    {
        tree[now].sum1 = tree[rson(now)].sum1 * tree[lson(now)].sum1;
        tree[now].sum2 = tree[rson(now)].sum2 * tree[lson(now)].sum2;
        return;
    }
    void Update1 ( int now, const Matrix &A, const Matrix &B )
    {
        tree[now].sum1 = B * tree[now].sum1 * A;
        tree[now].sum2 = B * tree[now].sum2 * A;
        tree[now].lazyl = tree[now].lazyl * A;
        tree[now].lazyr = B * tree[now].lazyr;
        return;
    }
    void Update2 ( int now )
    {
        swap(tree[now].sum1, tree[now].sum2);
        tree[now].rev ^= 1;
        return;
    }
    void Push_Down ( int now )
    {
        Update1(lson(now), tree[now].lazyl, tree[now].lazyr);
        Update1(rson(now), tree[now].lazyl, tree[now].lazyr);
        tree[now].lazyl.Identity();
        tree[now].lazyr.Identity();
        if ( tree[now].rev )
        {
            Update2(lson(now));
            Update2(rson(now));
            tree[now].rev = false;
        }
        return;
    }
    void Build ( int now, int l, int r )
    {
        tree[now].lazyl.Identity();
        tree[now].lazyr.Identity();
        tree[now].rev = false;
        if ( l == r )
        {
            if ( g[l].opt == 1 )
            {
                long double alpha = pi * g[l].C / 1800;
                long double c = cos(alpha), s = sin(alpha), x0 = g[l].A, y0 = g[l].B;
                tree[now].sum1.matrix[0][0] = c, tree[now].sum1.matrix[0][1] = -s, tree[now].sum1.matrix[0][2] = -c * x0 + s * y0 + x0;
                tree[now].sum1.matrix[1][0] = s, tree[now].sum1.matrix[1][1] = c, tree[now].sum1.matrix[1][2] = -s * x0 - c * y0 + y0;
                tree[now].sum1.matrix[2][0] = 0, tree[now].sum1.matrix[2][1] = 0, tree[now].sum1.matrix[2][2] = 1;
                alpha = -alpha;
                c = cos(alpha), s = sin(alpha), x0 = g[l].A, y0 = g[l].B;
                tree[now].sum2.matrix[0][0] = c, tree[now].sum2.matrix[0][1] = -s, tree[now].sum2.matrix[0][2] = -c * x0 + s * y0 + x0;
                tree[now].sum2.matrix[1][0] = s, tree[now].sum2.matrix[1][1] = c, tree[now].sum2.matrix[1][2] = -s * x0 - c * y0 + y0;
                tree[now].sum2.matrix[2][0] = 0, tree[now].sum2.matrix[2][1] = 0, tree[now].sum2.matrix[2][2] = 1;
            }
            else
            {
                long double A = g[l].A, B = g[l].B, C = g[l].C;
                tree[now].sum1.matrix[0][0] = B * B / ( A * A + B * B ), tree[now].sum1.matrix[0][1] = -A * B / ( A * A + B * B ), tree[now].sum1.matrix[0][2] = -A * C / ( A * A + B * B );
                tree[now].sum1.matrix[1][0] = -A * B / ( A * A + B * B ), tree[now].sum1.matrix[1][1] = A * A / ( A * A + B * B ), tree[now].sum1.matrix[1][2] = -B * C / ( A * A + B * B );
                tree[now].sum1.matrix[2][0] = 0, tree[now].sum1.matrix[2][1] = 0, tree[now].sum1.matrix[2][2] = 1;
                tree[now].sum2.matrix[0][0] = B * B / ( A * A + B * B ), tree[now].sum2.matrix[0][1] = -A * B / ( A * A + B * B ), tree[now].sum2.matrix[0][2] = -A * C / ( A * A + B * B );
                tree[now].sum2.matrix[1][0] = -A * B / ( A * A + B * B ), tree[now].sum2.matrix[1][1] = A * A / ( A * A + B * B ), tree[now].sum2.matrix[1][2] = -B * C / ( A * A + B * B );
                tree[now].sum2.matrix[2][0] = 0, tree[now].sum2.matrix[2][1] = 0, tree[now].sum2.matrix[2][2] = 1;
            }
            return;
        }
        int mid = l + r >> 1;
        Build(lson(now), l, mid);
        Build(rson(now), mid + 1, r);
        Push_Up(now);
        return;
    }
    void Insert_Matrix ( int now, int l, int r, int ql, int qr, const Matrix &A, const Matrix &B )
    {
        if ( l >= ql && r <= qr )
            { Update1(now, A, B); return; }
        Push_Down(now);
        int mid = l + r >> 1;
        if ( ql <= mid )
            Insert_Matrix(lson(now), l, mid, ql, qr, A, B);
        if ( qr > mid )
            Insert_Matrix(rson(now), mid + 1, r, ql, qr, A, B);
        Push_Up(now);
        return;
    }
    void Insert_Reverse ( int now, int l, int r, int ql, int qr )
    {
        if ( l >= ql && r <= qr )
            { Update2(now); return; }
        Push_Down(now);
        int mid = l + r >> 1;
        if ( ql <= mid )
            Insert_Reverse(lson(now), l, mid, ql, qr);
        if ( qr > mid )
            Insert_Reverse(rson(now), mid + 1, r, ql, qr);
        Push_Up(now);
        return;
    }
    Matrix Query ( int now, int l, int r, int ql, int qr )
    {
        if ( l >= ql && r <= qr )
            return tree[now].sum1;
        Push_Down(now);
        Matrix res;
        res.Identity();
        int mid = l + r >> 1;
        if ( qr > mid )
            res = res * Query(rson(now), mid + 1, r, ql, qr);
        if ( ql <= mid )
            res = res * Query(lson(now), l, mid, ql, qr);
        return res;
    }
}Tree;
int main ()
{
    freopen("point.in", "r", stdin);
    freopen("point.out", "w", stdout);
    scanf("%d%d", &n, &m);
    for ( int i = 1; i <= n; i ++ )
        scanf("%d%d%d%d", &g[i].opt, &g[i].A, &g[i].B, &g[i].C);
    Tree.Build(1, 1, n);
    int opt, l, r;
    long double u, v, w;
    Matrix upl, upr;
    while ( m -- )
    {
        scanf("%d", &opt);
        if ( opt == 1 )
        {
            scanf("%d%d%Lf%Lf", &l, &r, &u, &v);
            upl.matrix[0][0] = 1, upl.matrix[0][1] = 0, upl.matrix[0][2] = -u;
            upl.matrix[1][0] = 0, upl.matrix[1][1] = 1, upl.matrix[1][2] = -v;
            upl.matrix[2][0] = 0, upl.matrix[2][1] = 0, upl.matrix[2][2] = 1;
            upr = upl;
            upr.matrix[0][2] = u;
            upr.matrix[1][2] = v;
            Tree.Insert_Matrix(1, 1, n, l, r, upl, upr);
        }
        else if ( opt == 2 )
        {
            scanf("%d%d%Lf%Lf%Lf", &l, &r, &u, &v, &w);
            upl.matrix[0][0] = ( v * v - u * u ) / ( u * u + v * v ), upl.matrix[0][1] = -2 * u * v / ( u * u + v * v ), upl.matrix[0][2] = -2 * u * w / ( u * u + v * v );
            upl.matrix[1][0] = -2 * u * v / ( u * u + v * v ), upl.matrix[1][1] = ( u * u - v * v ) / ( u * u + v * v ), upl.matrix[1][2] = -2 * v * w / ( u * u + v * v );
            upl.matrix[2][0] = 0, upl.matrix[2][1] = 0, upl.matrix[2][2] = 1;
            upr = upl;
            Tree.Insert_Matrix(1, 1, n, l, r, upl, upr);
            Tree.Insert_Reverse(1, 1, n, l, r);
        }
        else
        {
            scanf("%d%d%Lf%Lf", &l, &r, &u, &v);
            upl.matrix[0][0] = u, upl.matrix[0][1] = upl.matrix[0][2] = 0;
            upl.matrix[1][0] = v, upl.matrix[1][1] = upl.matrix[1][2] = 0;
            upl.matrix[2][0] = 1, upl.matrix[2][1] = upl.matrix[2][2] = 0;
            upl = Tree.Query(1, 1, n, l, r) * upl;
            printf("%.8Lf %.8Lf\n", upl.matrix[0][0], upl.matrix[1][0]);
        }
    }
    return 0;
}

T2 有限域方阵期望对数转置相关度 (transpose)

神奇的线性代数，不会^_。

T3 灭国 (destroy)

首先明确题意，将普通队列换成优先队列求解 Bfs 序，可以加入 \(k\) 条边，需要最后的序列的字典序最大。

考虑模拟 Bfs 序的求解过程，由于当前队列 \(S_1\) 中最小的数可以通过加边暂时不被加入到 Bfs 序后，因此我们用集合 \(S_2\) 维护当前可以通过加边乱序加入到 Bfs 序的点，考虑下一次插入到 Bfs 序后的数，如果 \(S_1\) 中的最小的数小于 \(S_2\) 中最大的数并且 \(S_1\) 大小为 \(1\) ，那么将 \(S_1\) 中最小的数插入到 \(S_2\) 中，将 \(S_2\) 中最大的数插入到 \(S_1\) 中，如果大小不为 \(1\) ，直接将 \(S_1\) 中最小的数插入到 \(S_2\) 中即可，否则直接将 \(S_1\) 中最小的数加入到 Bfs 序中即可。

code

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <set>
#include <utility>
using namespace std;
const int max1 = 1e5;
int n, m, lim, degree[max1 + 5];
vector <int> edge[max1 + 5];
set <int> s1, s2;
vector < pair <int, int> > add_edge;
int last;
int main ()
{
    freopen("destroy.in", "r", stdin);
    freopen("destroy.out", "w", stdout);
    scanf("%d%d%d", &n, &m, &lim);
    for ( int i = 1, u, v; i <= m; i ++ )
    {
        scanf("%d%d", &u, &v);
        edge[u].push_back(v);
        ++degree[v];
    }
    for ( int i = 1; i <= n; i ++ )
        if ( !degree[i] )
            s1.insert(i);
    while ( true )
    {
        while ( s1.empty() && !s2.empty() )
        {
            int x = *--s2.end();
            s2.erase(--s2.end());
            add_edge.push_back(make_pair(last, x));
            printf("%d ", last = x);
            for ( auto v : edge[x] )
            {
                --degree[v];
                if ( !degree[v] )
                    s1.insert(v);
            }
        }
        if ( s1.empty() )
            break;
        int x = *s1.begin();
        s1.erase(s1.begin());
        if ( !s1.empty() && lim )
            s2.insert(x), --lim;
        else if ( !s2.empty() && x < *--s2.end() && lim )
        {
            int tmp = *--s2.end();
            s2.erase(--s2.end());
            s1.insert(tmp);
            add_edge.push_back(make_pair(last, tmp));
            s2.insert(x);
            --lim;
        }
        else
        {
            printf("%d ", last = x);
            for ( auto v : edge[x] )
            {
                --degree[v];
                if ( !degree[v] )
                    s1.insert(v);
            }
        }
    }
    printf("\n");
    printf("%lu\n", add_edge.size());
    for ( auto v : add_edge )
        printf("%d %d\n", v.first, v.second);
    return 0;
}