# BUAA-面向对象设计与构造 ——第一单元总结 #

呼，第一单元终于结束了 （披荆斩棘的一个月，来写一下三次作业大致的思路与总结吧٩( ╹▿╹ )۶。

第一单元的主题

第一单元的核心主题是表达式的括号展开，在保证去掉括号后所得到的表达式的正确性的同时做必要的化简，减少输出字符串的长度，以获取较好的性能。

对于表达式的正确理解（尤其是对指导书中的形式化表述的正确理解）我认为是这个单元的作业中构建代码架构的关键

Unit1一共分为三次作业，每次向上进行增量开发。

• 在第一次作业中，输入表达式中的括号至多一层，表达式其实就只是多项式，最后的输出表达式可以表达为以下的统一形式

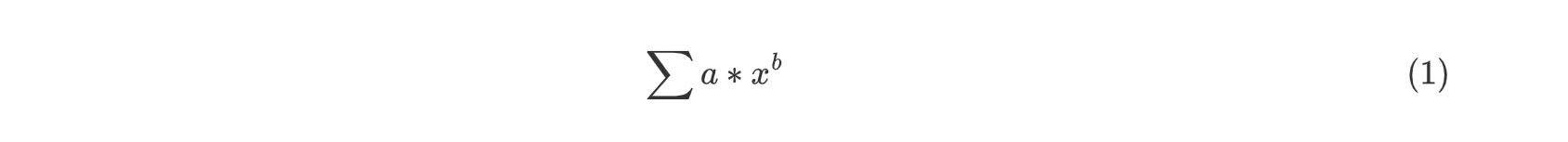
• 在第二次作业中，输入表达式中的多余括号至多一层。

  • 加入了自定义函数f(x,y,z)|g(x,y,z)|h(x,y,z)

  • 求和函数sum(i,s,e,<因子>)

  • 三角函数sin(<因子>) cos(<因子>)。

    对于其中的自定义函数调用式应代入形参展开，求和函数也应当作为和式展开。

    所以最后的输出表达式可以表达为以下的统一形式，要求其中的括号至多一层必要括号（指去掉该层括号之后，式子即不符合形式化表述）。

  

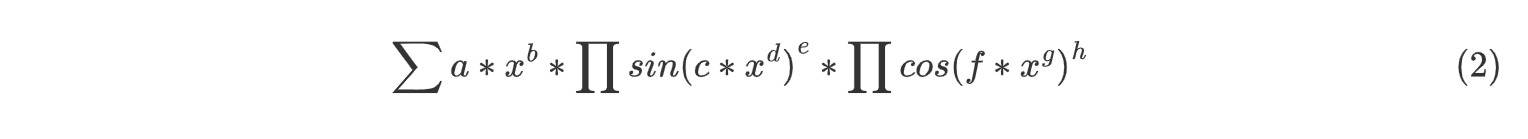
• 在第三次作业中，较第二次增加的部分有

  • 支持括号嵌套

  • 自定义函数调用式允许嵌套自定义函数和求和函数

  • 三角函数括号中的部分允许为表达式

    所以最后的输出表达式可以表达为以下的统一形式

  

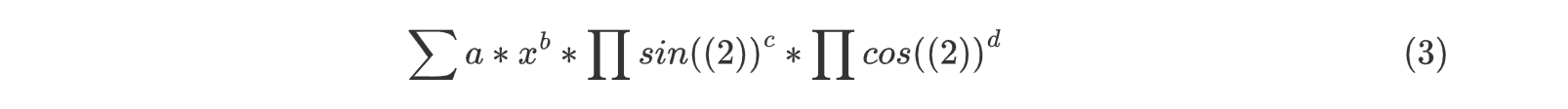
• 性能优化

  本质为减少输出字符串的长度，考虑合并同类项，以及某些特殊系数和指数所能带来的输出长度的减少。

  • 对于合并同类项，在采用HashMap进行存储时，如果其中的key是自己定义的类型，应重写HashCode和Equals方法，这样在调用put等方法时才是正确的。

  • 对于第二个方面，可做的优化有：

    • sin(0)==0 cos(0)==1

    • 1*x==x x**2==x**x

    • ()**0==1 x**1==x

       

三次作业的架构和思路

第一次作业

• 概览：

  由于假期过得过于开心（不可取!) ，到了学校的当晚才开始做pre作业，第一次作业发布后感觉完全没有思路，不知道从哪里下手，研究了好几天指导书才找到突破口：采用难度较低的预解析模式，作业也就随之转化为了针对输出的n个命令，整合出字符串的过程。

  在当时的思想上认为自己还是采用了面向对象的思维进行编码的，但现在回头看来，其实还是采用的数据结构的思维。虽然建了几个类，但更多的是像计组中的module的感觉，只是把要做的事分成了几部分，每个部分是传统意义上的函数的集合，仍没有构建表达式 项 因子等层级来进行管理。

• 预解析：

  在第一次发布的parser转换程序中，输入表达式转化为n个操作(暂且命名为operation）

  每一个操作的格式为：

  
  
  

  （其中方括号内部代表可选项）

  如：f1 sub x 1 f2 neg f1;

  由上述分析的(1)式的输出形式，因为只有x一个变量，所以存储系数和指数即可，因此抽象出了存储结果的容器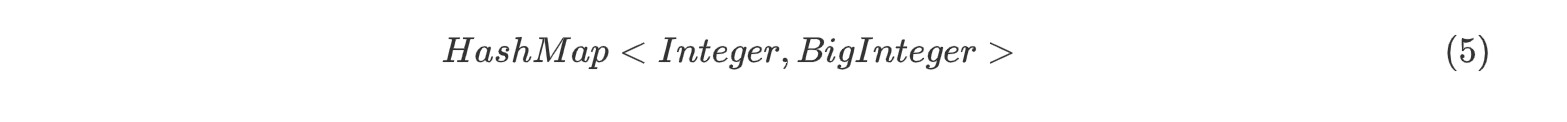

  

  <key,value>键值对中以Index作为索引，系数作为键值，有利于同类项的合并。

• 架构：

  通过上述分析，可以很自然的抽象出下述几个部分

  • Operation就是每一个操作，本质为一个HashMap

  • OperateNum为操作数，只可能为x |带符号有前导0的整数| 标签，因此分别设置了三个方法进行识别

  • OperateOp为操作符，即转换程序中对于+-^操作的标识符

  那么整个过程就变为了，从输入中读取操作，就新建一个Operation对象，然后解析操作数和操作符，丢给OperateOp进行计算，将得到的哈希表作为对象的属性。再存储到MainClas中设置的以<label,Operation>为键值对的哈希表中，若后续操作数为标签,便可以直接取用。

  重复上述过程，再调用PrintClass进行输出，即完成了作业。

 

 

• 代码度量

  采用MetricsReloded插件进行度量分析

  各个参数的含义可以参照这里

  class	OCavg	OCmax	WMC
  MainClas	6.0	6.0	6.0
  OperateNum	2.8333333333333335	8.0	17.0
  OperateOp	2.3333333333333335	4.0	14.0
  Operation	2.5	7.0	10.0
  PrintClass	8.0	9.0	16.0
  Total			63.0
  Average	3.3157894736842106	6.8	12.6

  method	CogC	ev(G)	iv(G)	v(G)
  OperateNum.isLabel(String)	0.0	1.0	1.0	1.0
  OperateNum.isNum(String)	0.0	1.0	1.0	1.0
  OperateNum.isVariable(String)	0.0	1.0	1.0	1.0
  OperateOp.pos(HashMap)	0.0	1.0	1.0	1.0
  OperateOp.sub(HashMap, HashMap)	0.0	1.0	1.0	1.0
  Operation.setOperateNums1(HashMap)	0.0	1.0	1.0	1.0
  Operation.setOperateNums2(HashMap)	0.0	1.0	1.0	1.0
  Operation.setType(String)	0.0	1.0	1.0	1.0
  OperateOp.neg(HashMap)	1.0	1.0	2.0	2.0
  OperateNum.getIndex(String)	2.0	2.0	2.0	2.0
  OperateNum.getOperateNums(String, HashMap>)	4.0	4.0	4.0	4.0
  OperateOp.add(HashMap, HashMap)	4.0	1.0	3.0	3.0
  OperateOp.pow(HashMap, HashMap)	4.0	2.0	3.0	3.0
  MainClas.main(String[])	7.0	1.0	6.0	6.0
  OperateOp.mul(HashMap, HashMap)	7.0	1.0	4.0	4.0
  Operation.calOperateNums()	7.0	7.0	7.0	7.0
  PrintClass.xiShuPrint(BigInteger)	11.0	1.0	7.0	7.0
  OperateNum.numChange(String)	16.0	6.0	7.0	9.0
  PrintClass.print(HashMap)	16.0	1.0	9.0	9.0
  Total	79.0	35.0	62.0	64.0
  Average	4.157894736842105	1.8421052631578947	3.263157894736842	3.3684210526315788

 

ev(G) 基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度， 使程序难于理解，可以看出其中最高的一个方法是关于计算的方法，由于其中调用了各类计算，所以其复杂 度仍可以理解。

iv(G) 模块设计复杂度是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味 模块耦合度高，PrintClass执行最终输出的化简，用了较多的判断语句，因此也是容易出现bug的地方

v(G) 是用来衡量一个模块判定结构的复杂程度，该数值较高的两个方法PrintClass和关于去除前导0的函数 numChange都是有较多的分支语句，调试出的问题也比较多。

• 评测

  由于预解析的存在，大大减少了bug出现的可能性，第一次作业在评测上较为顺利的通过了。

   

第二次作业

• 概览：

  采用预解析模式的分数会进行一定的折扣，同时由于每次作业都是迭代开发的原因，为保证第三次作业的实现，在第二次作业时选择了普通模式并进行了重构（通宵真的太肝了），得益于实验和训练代码的启发以及第一次作业互测时同屋同学的代码，有了大致可以参考的架构。

• 递归下降：

  一开始看training中的代码其实没太看明白，后来试着去搜索了Parser和Lexer后，找到了这篇文章，便对递归下降和指导书中的形式化表述有了些理解。或者说，这个时候才明白了形式化表述在表达些什么。在我的理解中，它应该在告诉我们以怎样的视角去分隔输入，核心应该是——符号。

  Parser和Lexer这两个类其实便充当了解析的角色，先用Lexer进行字符串的扫描输入，可以理解为扫出的每一个Token 就是一个式子中的基础元素，然后Parser通过规定的文法，识别不同的符号在连接时，我们应该去得到的规定的元素是什么，是表达式还是项还是因子，在得到之后就去建立一棵表达式树。

  就像前面提到的，由于核心是符号，我的Parser中的方法划分其实就可以对应到不同的符号:

  • parserExpr----> '+'

  • parserTerm----> '*'

  • parserPow----> '^'

  然后就在该方法中调用与之对应的Operate类中的各方法（已实现了同类项合并），这样到得到最后的哈希表的时候，就已经是一个化简完了的表达式了。

• 数据存储：

  在解决完解析问题后，另外一个大的问题就是数据的存储，这里沿用了第一次作业的思路，既然最后输出的只会有一个自变量，那么就抽出(2)中的所有有关数据，作为一个存储的容器。

  
  
  

  public class Base {
      private BigInteger index; //前为指数，后为系数
      private HashMap<ArrayList<BigInteger>, BigInteger> sinAttrs;// 前为括号内容，后为指数
      private HashMap<ArrayList<BigInteger>, BigInteger> cosAttrs;
  }

  出于合并同类项的考虑，同样都是把系数抽离，以作为value。

  关于这个存储方式的优劣讨论暂且按下不表，后文会再提到的。

• 自定义函数和求和函数：

  采用了正则表达式的方式，识别出自定义函数和求和函数，并通过simplified类，将这两个部分展开后带括号后放回原表达式交由Parser解析（可支持括号嵌套

  注意：自定义函数调用的代入应当为数学代入，因此应该加括号

• 架构：

  

   

• 代码度量

  class	OCavg	OCmax	WMC
  Base	1.6	4.0	8.0
  Lexer	3.0	5.0	15.0
  MainClass	3.0	3.0	3.0
  OperateNum	1.6666666666666667	3.0	5.0
  OperateOp	5.0	9.0	20.0
  Parser	4.4	8.0	22.0
  SelfDefined	4.5	8.0	9.0
  Simplified	4.0	5.0	12.0
  ToStr	9.5	13.0	19.0
  Total			113.0
  Average	3.7666666666666666	6.444444444444445	12.555555555555555

  method	CogC	ev(G）	iv(G)	v(G)
  Base.Base(BigInteger, HashMap, BigInteger>, HashMap, BigInteger>)	0.0	1.0	1.0	1.0
  Base.equal(Base)	6.0	4.0	3.0	4.0
  Base.getCosAttrs()	0.0	1.0	1.0	1.0
  Base.getIndex()	0.0	1.0	1.0	1.0
  Base.getSinAttrs()	0.0	1.0	1.0	1.0
  Lexer.getCurToken()	0.0	1.0	1.0	1.0
  Lexer.getNum()	6.0	3.0	5.0	6.0
  Lexer.getSinCos()	4.0	3.0	3.0	4.0
  Lexer.Lexer(String)	0.0	1.0	1.0	1.0
  Lexer.next()	6.0	2.0	4.0	6.0
  MainClass.main(String[])	4.0	1.0	3.0	3.0
  OperateNum.getBacket()	4.0	1.0	3.0	3.0
  OperateNum.getoNattrs()	0.0	1.0	1.0	1.0
  OperateNum.setoNattrs(HashMap)	0.0	1.0	1.0	1.0
  OperateOp.add(HashMap, HashMap)	9.0	4.0	6.0	6.0
  OperateOp.mul(HashMap, HashMap)	25.0	1.0	9.0	9.0
  OperateOp.neg(HashMap)	1.0	1.0	2.0	2.0
  OperateOp.pow(HashMap, int)	4.0	1.0	3.0	3.0
  Parser.parseExpr()	8.0	1.0	6.0	6.0
  Parser.parseFactor()	13.0	1.0	8.0	9.0
  Parser.parsePow()	6.0	1.0	4.0	4.0
  Parser.Parser(Lexer)	0.0	1.0	1.0	1.0
  Parser.parseTerm()	4.0	1.0	4.0	4.0
  SelfDefined.SelfDefined(HashMap)	0.0	1.0	1.0	1.0
  SelfDefined.sim(String)	15.0	4.0	7.0	8.0
  Simplified.getSumDefined(String)	7.0	5.0	3.0	5.0
  Simplified.simFunc(String, HashMap)	1.0	1.0	2.0	2.0
  Simplified.simSum(String)	12.0	1.0	5.0	5.0
  ToStr.addAttr(HashMap, Base)	11.0	1.0	6.0	6.0
  ToStr.print(HashMap)	17.0	4.0	13.0	13.0
  Total	163.0	51.0	109.0	118.0
  Average	5.433333333333334	1.7	3.6333333333333333	3.933333333333333

• 测试

  由上面的度量分析可以看到，指数较高的部分都集中在ToStr以及 mul这两个部分，而实际调试和测试过程中出现问题较多的也是这两个部分。输出时为了追求性能，用了简单的字符串替换，将1*x等替换成了x，但忽略了前缀或是后缀情况，如101*x被替换后就变为了10x，不符合正确的形式化表述。

  （强测和互测都是这个问题

  而在mul这个函数中发现了深浅拷贝的问题，以及在遍历容器的过程中不能直接进行remove操作，否则会抛出CurrentNotification的错误，因为keyset()已经被改变，正确做法是先将遍历容器eg:map1进行一个深拷贝得到一个result容器，然后对result使用remove方法。

   

第三次作业

• 概览：

  由于增加了三角函数内部的嵌套，原有的纯数据类型的存储方式变得不可取，但是思想仍然可以沿用，存储结构依然是一个哈希表，不过需要进行一点修改

  

• 关于面向对象：

  可能直到最后一次作业才真的带有了一点面向对象思想的色彩，之前的作业忽视了因子本身的特点，把他们全部同质化提取出了共同的部分，这样的数据结构架构有以下几个问题：

  • 代码间的耦合度过高，由于全部都是没有进行封装的裸露的数据，导致嵌套层次太多，从最后的哈希表到Base类，再展开其中的属性，对于里面的三角函数还需要再一步进行展开，大大增加了调试过程中的难度，同时代码的延拓性差，导致第三次作业也进行了较大的修改，否则由于表达式可以作为三角函数内部因子的原因，会使内部的嵌套层次进一步变深，实现过程中碰到的问题也会更多。

  • 由于没有抽象出类，没有把任务按照小的部分进行分配，把需要实现的特定功能（如输出），全部聚合在了一个类似于ToStr的类中进行考虑，这样的话就会有很多循环和分支的判定，并且难以定位错误的位置，概括而言就是没有"各司其职"。

  为了解决这些问题，又去重新分析了文法，设置了Expr Term SinCos Variable四个类，同时实现了Basic接口，在每个类中重写了toString方法（较上次作业的优点是，调试时看到的就是输出时的情况，不再是纯粹数据还要依靠人去翻译），同时这样就做到了把一个大的任务分给了不同的角色去完成，只要保证每个模块的正确性，就能保证这个大任务的正确性，这是一个很朴素直观的道理（有点继承计组中冲突冒险模块测试用例的构建，但是不太容易想起）。

• 架构：

  除了存储模块这一块外，基本沿用了第二次作业的架构，UML类图如下：

  

   

   

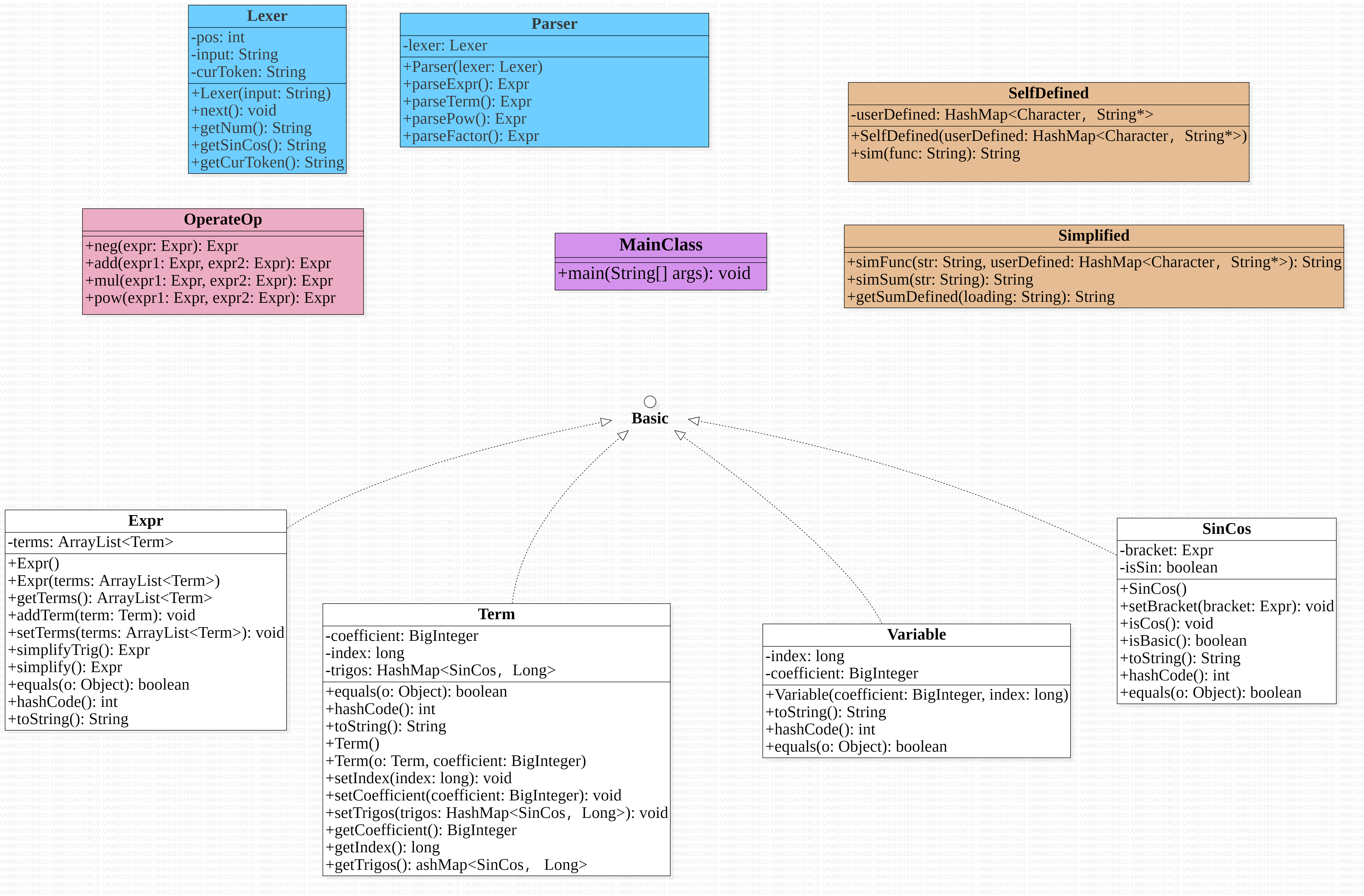
• 代码分析：

利用Metrics进行度量分析

class	OCavg	OCmax	WMC
Expr	2.9	7.0	29.0
Lexer	3.0	5.0	15.0
MainClass	3.0	3.0	3.0
OperateOp	4.25	6.0	17.0
Parser	4.0	7.0	20.0
SelfDefined	4.5	8.0	9.0
Simplified	4.666666666666667	5.0	14.0
SinCos	3.4285714285714284	9.0	24.0
Term	2.1818181818181817	12.0	24.0
Variable	2.75	6.0	11.0
Total			166.0
Average	3.1923076923076925	6.8	16.6

 

method	CogC	ev(G）	iv(G)	v(G)
Expr.Expr()	0.0	1.0	1.0	1.0
Expr.Expr(ArrayList)	0.0	1.0	1.0	1.0
Expr.addTerm(Term)	0.0	1.0	1.0	1.0
Expr.getTerms()	0.0	1.0	1.0	1.0
Expr.hashCode()	0.0	1.0	1.0	1.0
Expr.setTerms(ArrayList)	0.0	1.0	1.0	1.0
Lexer.Lexer(String)	0.0	1.0	1.0	1.0
Lexer.getCurToken()	0.0	1.0	1.0	1.0
Parser.Parser(Lexer)	0.0	1.0	1.0	1.0
SelfDefined.SelfDefined(HashMap)	0.0	1.0	1.0	1.0
SinCos.SinCos()	0.0	1.0	1.0	1.0
SinCos.hashCode()	0.0	1.0	1.0	1.0
SinCos.isCos()	0.0	1.0	1.0	1.0
SinCos.setBracket(Expr)	0.0	1.0	1.0	1.0
Term.Term()	0.0	1.0	1.0	1.0
Term.Term(Term, BigInteger)	0.0	1.0	1.0	1.0
Term.getCoefficient()	0.0	1.0	1.0	1.0
Term.getIndex()	0.0	1.0	1.0	1.0
Term.getTrigos()	0.0	1.0	1.0	1.0
Term.hashCode()	0.0	1.0	1.0	1.0
Term.setCoefficient(BigInteger)	0.0	1.0	1.0	1.0
Term.setIndex(long)	0.0	1.0	1.0	1.0
Term.setTrigos(HashMap)	0.0	1.0	1.0	1.0
Variable.Variable(BigInteger, Long)	0.0	1.0	1.0	1.0
Variable.hashCode()	0.0	1.0	1.0	1.0
OperateOp.neg(Expr)	1.0	1.0	2.0	2.0
Expr.equals(Object)	3.0	3.0	2.0	4.0
Parser.parsePow()	3.0	1.0	3.0	3.0
Lexer.getSinCos()	4.0	3.0	3.0	4.0
MainClass.main(String[])	4.0	1.0	3.0	3.0
OperateOp.pow(Expr, long)	4.0	1.0	3.0	3.0
Parser.parseTerm()	4.0	1.0	4.0	4.0
SinCos.equals(Object)	4.0	3.0	3.0	5.0
Term.equals(Object)	4.0	3.0	4.0	6.0
Variable.equals(Object)	4.0	3.0	3.0	5.0
Lexer.getNum()	6.0	3.0	5.0	6.0
Lexer.next()	6.0	2.0	4.0	6.0
Simplified.getSumDefined(String)	7.0	5.0	3.0	5.0
Variable.toString()	7.0	3.0	5.0	6.0
Parser.parseExpr()	8.0	1.0	6.0	6.0
Expr.simplifyTrig()	9.0	4.0	7.0	7.0
Simplified.simFunc(String, HashMap)	9.0	1.0	9.0	9.0
Expr.simplify()	10.0	4.0	7.0	7.0
OperateOp.add(Expr, Expr)	10.0	4.0	7.0	7.0
Parser.parseFactor()	10.0	1.0	8.0	8.0
SinCos.toString(Long)	10.0	4.0	5.0	8.0
Expr.toString()	11.0	4.0	7.0	7.0
Simplified.simSum(String)	12.0	1.0	5.0	5.0
OperateOp.mul(Expr, Expr)	14.0	1.0	6.0	6.0
SelfDefined.sim(String)	15.0	4.0	7.0	8.0
Term.toString()	19.0	10.0	10.0	12.0
SinCos.isBasic()	21.0	9.0	6.0	9.0
Total	219.0	106.0	162.0	186.0
Average	4.211538461538462	2.0384615384615383	3.1153846153846154	3.576923076923077

可以看到Term中的toString方法仍然有较高的复杂度，有待优化。还有SinCos中用于判断最外层括号内部的内容是否只为常数或只为幂函数，这样可以少套一层括号，该方法中使用了大量的分支语句，导致了CogC有较高的值

Statistics插件分析：

（最后总行数也到了908 QAQ）

 

• 评测

  针对所有的测试，都可以复用解析时采取的思路，每次测试一个抽象层面的类，先测试不同的基础因子能否通过测试，再将它们向上构造，利于保证完备性。这可能正是互测时采用cost限制的原因，即便是很复杂的式子，其在测出问题的时候可能也就是到最底层中的一个问题。

  比如屡试不爽的sin((-x)**2)**2

  这次作业的课下测试没有做的太好，交上去过了中测就以为万事大吉了(orz)，在识别自定义函数部分，没有做好迭代的测试，与上次作业使用的方法是相同的，在提取实参时，由于使用了,作为split函数的分隔符，导致在嵌套过程中出现bug

  如f(f(x,x**2),3)就会被分割为f(x |x**2)| 3三个部分，这显然不是我们想要的，所以修改了自定义函数部分的代码，采用递归，找到最内层的函数调用替换后，再往上替换

  for (如果有自定义函数调用) {
              if ("fgh".indexOf(simStr.charAt(i)) != -1) {
                  char s = simStr.charAt(i);
                  SelfDefined func = new SelfDefined(userDefined);
                  String funcCall = getSumDefined(simStr.substring(i));
                  String funCall2 = funcCall;
                  while (存在嵌套调用) {
                      Simplified simplified = new Simplified();
                      funcCall = funcCall.charAt(0) + simplified.simFunc(
                              funcCall.substring(1), userDefined);
                  }
                  String simFunc = func.sim(funcCall); // 把自定义函数因子代入化简后再返回，记得加括号
                  simStr = simStr.replace(funCall2, simFunc);
              }
          }
          return simStr;// 新字符串中不再出现自定义函数
      }

  另外的错误就是求和函数中的数据边界问题，在指导书中并没有规定到一定是int的范围，就踏入了固定的框中，导致数据溢出（五次hack都是这个问题），另外一个方面也反映出了互测时大家测试的方向有一定的相似性

 

一些思考

可能是由于Pre作业中提到了正则表达式的原因，通过这几次作业的互测代码可以看出大家还是很喜欢利用正则表达式来做一些事情的，但是在构造数据不充分的情况下，正则表达式非常非常非常非常容易出bug。例如没有想到的作为前缀或者后缀的情况。如[fgh]\\([^fgh]*\\)就可以匹配到f(x)*sin(x)

另外一个方面，正则表达式的可扩展性不高，它的定制化程度很强，为了精准匹配所以边界通常设的很窄，但是当出现新的需求的时候，就会有意想不到的问题。

这个时候采用数据结构的知识（比如用栈匹配括号）或者用解析的方法单独讨论应该会更好。

 

写在最后的话

没想到这学期因为OO上来就有了一种深入考期的感觉，焦虑崩溃周周复始，靠着写博客的星期略微懈怠。

要感谢每一个帮助我陪我破防的人

还有就是

希望安全挺过下一个单元o(TヘTo)