BZOJ 2301 HAOI2011 Problem b 莫比乌斯反演

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=2301

 

题意概述：

　　对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k。

　　1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000.

 

分析：

　　这实际上就是莫比乌斯反演的裸题！

　　但是我为什么要专门发出来呢？

　　因为我想总结一下代码的问题和一般思路......

 

　　首先观察题目询问，可以发现询问可以用矩形前缀和来回答。于是问题简化为给出a,b,k，求gcd(x,y)=k的数对数量，1<=x<=a,1<=y<=b。

　　我们令函数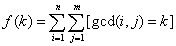，这就是我们的计算目标，但是显然这个东西求起来非常的麻烦啊！！评测不能承受之慢啊！！！

　　于是我们考虑莫比乌斯反演，构造一个更加简单易求的函数F(k)，F(k)可以由f(d)（F有两种考虑方向，k|d或者d|k）得到。

　　考虑两种构造的方式，最后构造出来的F(k)意义为一定范围内k|gcd(x,y)的(x,y)的对数，。

　　其中F(k)是非常好求的，。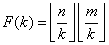

　　根据莫比乌斯反演，我们得到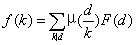：，即。

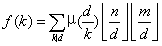　　可以发现其中d/k的值一定是连续的，不妨令n<=m，那么我们可以把这个柿子变成：。

　　同时我们发现n最多有2*sqrt(n)种被整除的结果，于是我们只需要维护一个μ的前缀和就可以大幅提高询问的效率，利用经典方法在O(sqrt(N))的时间内回答单组询问（具体讲解见代码注释）。

　　时间复杂度O(N*sqrt(N))。

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<cctype>
using namespace std;
const int maxn=50005;
const int maxp=5200;
typedef long long LL;

int N,a,b,c,d,k;
int pri[maxp],tot,mu[maxn],sum[maxn]; bool ntp[maxn];

void get_mu()
{
    ntp[0]=ntp[1]=1,mu[1]=1;
    for(int i=2;i<=50000;i++){
        if(!ntp[i]) pri[++tot]=i,mu[i]=-1;
        for(int j=1;j<=tot&&1ll*pri[j]*i<=50000;j++){
            ntp[pri[j]*i]=1;
            if(i%pri[j]==0){ mu[i*pri[j]]=0; break; }
            mu[i*pri[j]]=-mu[i];
        }
    }
    for(int i=1;i<=50000;i++) sum[i]=sum[i-1]+mu[i];
}
LL calc(int n,int m)
{
    if(n>m) swap(n,m);
    n/=k,m/=k;
    LL re=0;
    for(int i=1,last=0;i<=n;i=last+1){
        last=min(n/(n/i),m/(m/i));//令x=n/i，那么可以发现n/x=max{i|n/i=x}，只要n/i和m/i中间有一个变化了F(d)就会改变，所以取min。
        re+=1ll*(sum[last]-sum[i-1])*(n/i)*(m/i);//因为n最多被乘除的结果最多有2*sqrt(N)种，所以单次询问复杂度O(sqrt(N))。
    }
    return re;
}
int main()
{
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    get_mu();
    scanf("%d",&N);
    for(int i=1;i<=N;i++){
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        printf("%lld\n",calc(b,d)-calc(a-1,d)-calc(b,c-1)+calc(a-1,c-1));
    }
    return 0;
}