上海理工大学第二届“联想杯”全国程序设计邀请赛 J.JXC&Jesus（线性筛）

• 题目：JXC&Jesus
• 解析：首先此题的时间复杂度要求是O（n），不过官方题解还是不太懂，先把这种O（n*logn）的写一下（一样可以A掉题目，数据问题而已）；
  从X / f(x, m)可以得推出f(x, m)的值（一定好好学latex...）,最后得到结果
  

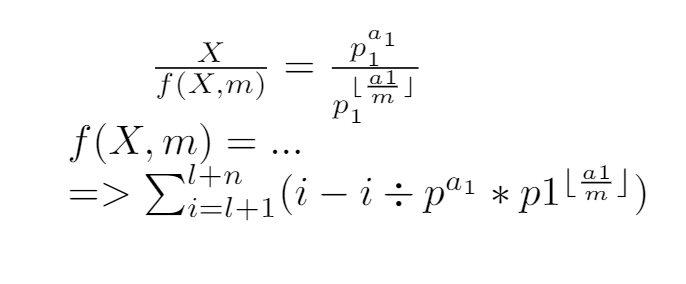
根据题目所给的式子发现，最终式子里需要求出组成x的第一个质数并统计出其指数个数，可以在线性筛筛素数的过程记录组成x的第一个质数是谁，若x为素数，则p1 = x, a1 = 1；否则在线性筛的过程中，实际上筛出的合数都是由其最小的质数和某个数将其筛出，也就是构成i * prime[j]的最小质数为prime[j]，然后再用常规操作算出其指数部分即可

• 代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e7 + 5;
int n, m, l;
int prime[N], vis[N], cnt = 0, minp[N];
ll res = 0;
ll qpow(ll a, ll x)
{
    ll ans = 1;
    while(x)
    {
        if(x & 1) ans = ans * a;
        a = a * a;
        x >>= 1;
    }
    return ans;
}
void init()
{
    vis[0] = vis[1] = 1;
    for(int i = 2; i < N; i++)
    {
        if(!vis[i])
        {
            minp[i] = i; //最小的质数为自己本身
            prime[++cnt] = i;
        }
        for(int j = 1; j <= cnt && i * prime[j] < N; j++)
        {
            vis[i * prime[j]] = 1;
            minp[i * prime[j]] = prime[j]; //记录组成i * prime[j]的最小的质数
            if(i % prime[j] == 0) break;
        }
    }
}
ll solve(ll x)
{
    ll num = 0, minPrime = minp[x], i = x;
    if(minPrime == x) num = 1;
    else
    {
        while(x % minPrime == 0)
        {
            x /= minPrime;
            num ++; //统计a1（指数）的个数
        }
    }
    ll ans =  i / qpow(minPrime, num) * qpow(minPrime, num / (ll)m);
    return ans;
}
int main()
{
    init();
    cin >> n >> m >> l;
    for(int i = l + 1; i <= l + n; i++)
        res += i - solve((ll)i);
    cout << res << endl;
    return 0;
}