题解 D. The Pool "蔚来杯"2022牛客暑期多校训练营7
出题人的题解实在是无法令人恭维,特此写一份自己的题解
【大意】
\(T\) 次询问,每次询问给定 \(n, m(1\leq n,m\leq 10^{18})\) ,问长宽分别为 \(n, m\) 的矩形顶点摆放在整点后;所有不同摆放方案中,每个方案完全包含的 \(1\times 1\) 格子数量的和是多少?
我们认为两个方案不同,当且仅当一个方案的矩形无法仅通过平移变换,得到另一个方案。
【分析】
我们将矩形 \(ABCD\) 的一个顶点放置在原点上,设 \(AB=n, AD=m\) ,则 \(B\) 点的点坐标需要满足 \(x_B^2+y_B^2=n^2\)
如果我们能找到所有满足条件的点坐标,那它们显然都是答案的候选(可能有的方案能通过别的方案平移得到、有的方案无法使得 \(D\) 在整点)
因此,当前的问题即是:给定 \(l\) ,如何求解所有满足 \(x_B^2+y_B^2=l\) 的点
转化一下问题,由于二维平面上的整点能唯一地对应复平面上,满足 \(\Re z, \Im z\in Z\) 的所有复数 \(z\) 。因此,我们可以直接以高斯整数 \(Z[i]\) 的方式描述待求问题:
求解有多少个高斯整数 \(z=x_B+i\cdot y_B\) ,使得 \(z\cdot \bar z=l\)
我们考虑将 \(l\) 进行质因数分解,显然可以将 \(l\) 分解为 \(\displaystyle l=2^{c_2}\cdot \prod_j p_j^{k_j} \cdot \prod_j q_j^{t_j}\) 的形式,其中 \(c_2\geq 0, k_j, t_j>0, q_j\) 为 \(4n+3\) 型质数,\(p_j\) 为 \(4n+1\) 型质数
根据高斯质数的规律,\(2=(1+i)(1-i), q_j\) 无法继续分解,而 \(p_j\) 能进一步分解为两个共轭的高斯质数 \((a+bi),(a-bi)\) 的乘积
为了对 \(p_j\) 进行高斯质数意义上的质因数分解,我们可以随机一个 \(t\neq 0\pmod {p_j}\) ,再令 \(\displaystyle k=t^{p_j-1\over 4}\bmod p_j\) 。根据二次剩余的理论,\(k^2\equiv \pm 1\pmod {p_j}\) ,取值为 \(-1\) 的概率恰为 \({1\over 2}\) 。
所以,我们期望两次随机,就能选出一个 \(k\) ,使得 \(k^2\equiv -1\pmod {p_j}\) ,即 \(p_j\mid (k^2+1)\) 。由于在 \(Z[i]\) 上,\(k^2+1=(k+i)(k-i)\) ,故有 \(p_j\mid (k+i)(k-i)\)
而 \(k, 1<p_j\) ,能推出不存在 \(z\in Z[i]\) 使得 \(p_j\cdot z=k+i\) ,从而 \(p_j\) 并不整除 \(k+i\) ,同理 \(p_j\) 并不整除 \(k-i\) ;所以 \((a+bi), (a-bi)\) 其中一者整除 \(k+i\) ;又因为两者均是高斯质数,不可再分解;故直接求解 \(\gcd(p_j, k+i)\) 即可得到两者之一,再用 \(p_j\) 除即可再得到另一个解
根据上述理论,我们可以将 \(l\) 进一步分解为 \(\displaystyle l=(1+i)^{c_2}\cdot (1-i)^{c_2}\cdot \prod_j (a+bi)^{k_j}(a-bi)^{k_j}\cdot \prod_j q_j^{t_j}\) ,我们需要求解有多少个高斯整数 \(z\) 使得 \(z\cdot \bar z=l\)
简单起见,我们不妨先考虑不含因子 \(2\) 的情况:
对于 \((a+bi)\) 与 \((a-bi)\) 型的高斯质数,我们显然每次需要将其中一个分配给 \(z\) ,另一个分配给 \(\bar z\) ,才能使得两者保持共轭的性质;因此我们可以枚举 \((a+bi)\) 中,有 \(t(0\leq t\leq k_j)\) 个分配给了 \(z\) ,剩下的分配给了 \(\bar z\) ;因此 \(z\) 中的方案为 \((a+bi)^t\cdot (a-bi)^{k_j-t}\) ,方案数为 \(k_j+1\)
对于 \(q_j^{t_j}\) 型高斯质数,当且仅当 \(t_j\) 为偶数时可以平分给 \(z\) 与 \(\bar z\) ,产生唯一的方案;否则分配是不平均的,方案数为 \(0\)
由于式子 \(z\cdot \bar z=m=n^2\) ,故方案数必然不为 \(0\) ;然而对于每个求解出的合法解 \(z\) ,我们乘上单位数 \(1, i, -1, -i\) ,并向 \(\bar z\) 乘上相应单位数的共轭,都能得到一组互不相同的解(相伴解);因此我们即可得出所有的合法方案,方案数为 \(\displaystyle 4\prod_j (k_j+1)\)
对于含 \(2\) 因子时,同样我们可以考虑分配多少个 \((1+i)\) 给 \(z\) ,剩下的给 \(\bar z\) ;然而两者交换一个 \((1+i),(1-i)\) 后,我们发现答案实际上只相差一个 \(i\) ,这个的贡献其实在后续乘单位数中已经进行了消除;为此,我们不妨将所有的 \((1+i)\) 分配给 \(z\) ,因为其不影响方案数
根据题解,方案数为 \(\displaystyle 4\prod_j(k_j+1)\) ,最大值为 \(4\times 295245\) ,在 \(n=495229111954868525\) 时取得
现在,我们已经求解所有满足 \(x_B^2+y_B^2=l\) 的点,需要在这些候选点中,选择无法通过别的方案平移得到、\(D\) 在整点的方案
对于 \(n=m\) 的情况,显然,角 \(\angle BAx\in [0, {\pi\over 2})\) 都对应互不相同的矩形。我们从候选点中,选择那些 \(\Im z\geq 0\wedge \Re z>0\) 的解即可。
而对于 \(n\neq m\) 的情况,角 \(\angle BAx\in[0, \pi)\) 都对应互不相同的矩形;同理可以从候选点中,选择 \(\Im z>0\vee (\Im z=0\wedge \Re z>0)\) 的解。
那如何确认候选点 \((a+bi)\) 是否满足 \(D\) 也位于整点呢?
根据几何关系,我们直接将候选点乘上单位数 \(i\) 即可旋转 \({pi\over 2}\) ,再乘上 \({m\over n}\) 即可放缩至 \(D\) 点;因此只需要验证 \((a+bi)\cdot i\cdot {m\over n}\) 是否为整点即可
终于来到了最终答案求解的部分,已知 \(B\) 位于 \((a'+b'i)\) ,\(D\) 位于 \((c'+d'i)\) ,如何求解答案包含的 \(1\times 1\) 格子数量的和?
为了方便,我们不妨假设 \(a=|a'|, b=|b'|, c=|c'|, d=|d'|\) ,它们有几何关系如下:

我们按下述方法分别统计每个三角形对答案的贡献
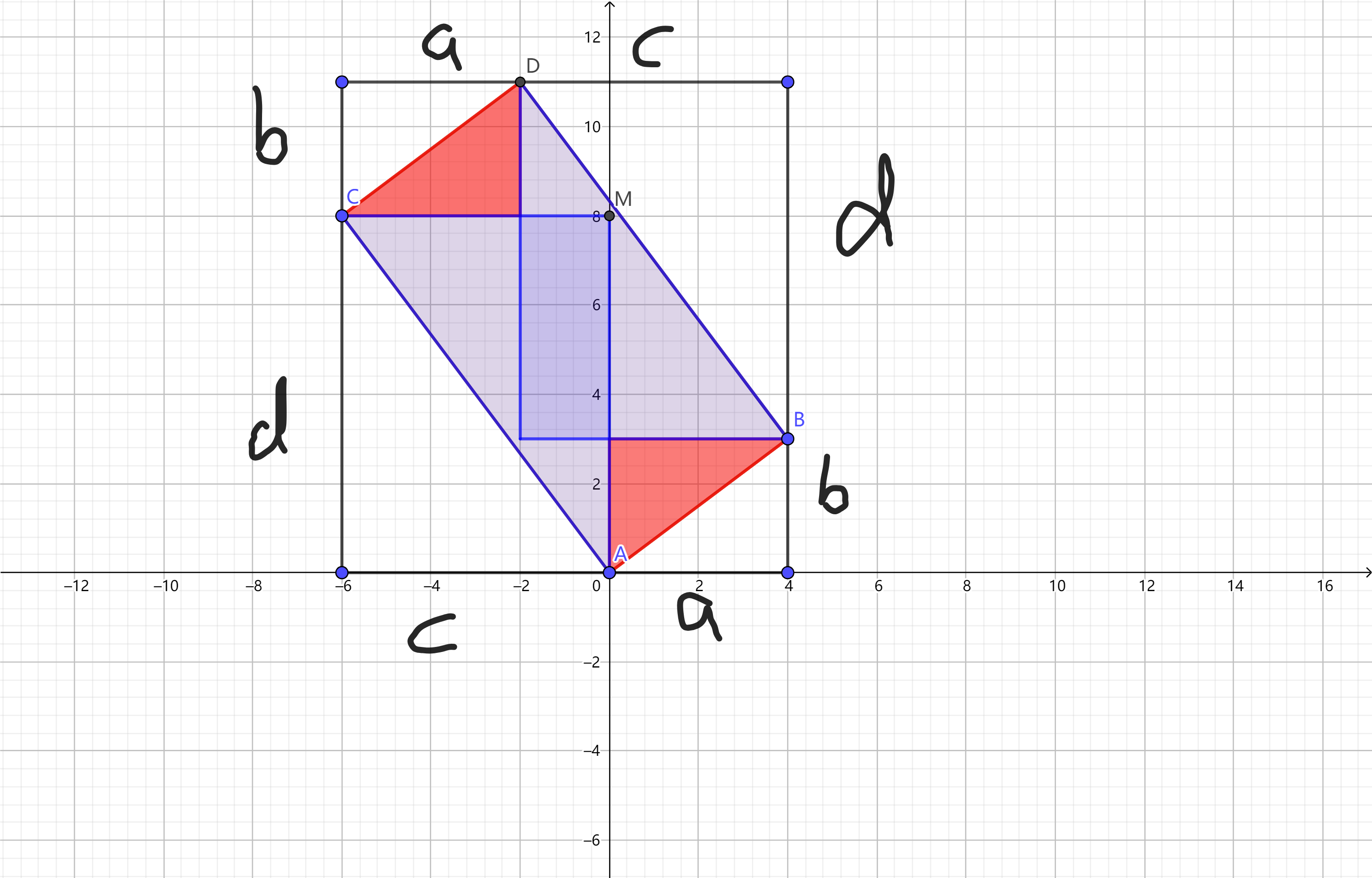
红色三角形的贡献是 \(y={b\over a}x,x\in[0, a]\) 内的格子数,蓝色的是 \(y={d\over c}x,x\in[0, c]\) 内的格子数,很显然,有一部分会被重复计算或遗漏,需要再扣除一个 \((c-a)(d-b)\)
而关于三角形内部的贡献,我们考虑直线的斜率是不少于 \(0\) 的,因此只要格子的左上端点位于直线 \(y={b\over a}x\) 下方(或线上)则能被统计到
故答案变为:除最下行、最右列外,直线下方的整点数
显然是可以由类欧或万欧解决,这里介绍一下 pick 定理的解法:
对于这类所有顶点都在整点上的多边形,称为格点多边形,其面积满足公式:\(S={1\over 2}B+I-1\) ,其中 \(B\) 为边缘点数,\(I\) 为多边形内部点数
该直线面积显然为 \({ab\over 2}\) ,边缘点数可以发现是 \((a+1)+(b+1)+(\gcd(a,b)+1)-3=a+b+\gcd(a,b)\) ,故内部点数为 \(I={ab-a-b-\gcd(a,b)\over 2}+1\)
而可以发现,格子的左上端点仅由内部点、斜线上的非端点构成;因此格子数为 \(I+\gcd(a,b)-1={ab-a-b+\gcd(a,b)\over 2}\)
综上,我们可以先对 \(n\) 进行 Pollard_Rho 算法进行质因数分解;暴力求解所有高斯整数后,选出合法点,并利用上述公式求解答案。
【代码】
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mp make_pair
#define de(x) cout << #x <<" = "<<x<<endl
#define dd(x) cout << #x <<" = "<<x<<" "
mt19937 rnd(time(0));
const int P=998244353;
inline __int128 absl(__int128 x) { return x<0?-x:x; }
inline ll kpow(ll a, ll x, ll p) { ll ans=1; for(;x;x>>=1, a=(__int128)a*a%p) if(x&1) ans=(__int128)ans*a%p; return ans; }
struct Zi {
__int128 re, im;
inline Zi (ll re_=0, ll im_=0):re(re_), im(im_) {}
inline Zi& operator += (const Zi &rhs) { re+=rhs.re; im+=rhs.im; return *this; }
inline Zi& operator -= (const Zi &rhs) { re-=rhs.re; im-=rhs.im; return *this; }
inline Zi& operator *= (const Zi &rhs) { tie(re, im)=mp(re*rhs.re-im*rhs.im, re*rhs.im+im*rhs.re); return *this; }
inline Zi& operator /= (const Zi &rhs) {
__int128 r=rhs.re, i=rhs.im, l=r*r+i*i;
tie(r, i)=mp(2*(re*r+im*i)+l, 2*(im*r-re*i)+l); l*=2;
if(r<0) re=-((-r+l-1)/l);
else re=r/l;
if(i<0) im=-((-i+l-1)/l);
else im=i/l;
return *this;
}
inline Zi& operator %= (const Zi &rhs) { Zi tmp=*this; tmp/=rhs; tmp*=rhs; return *this-=tmp; }
inline Zi operator + (const Zi &rhs) const { Zi lhs=*this; return lhs+=rhs; }
inline Zi operator - (const Zi &rhs) const { Zi lhs=*this; return lhs-=rhs; }
inline Zi operator * (const Zi &rhs) const { Zi lhs=*this; return lhs*=rhs; }
inline Zi operator / (const Zi &rhs) const { Zi lhs=*this; return lhs/=rhs; }
inline Zi operator % (const Zi &rhs) const { Zi lhs=*this; return lhs%=rhs; }
};
inline Zi kpow(Zi a, ll x) { Zi ans=1; for(;x;x>>=1, a=a*a) if(x&1) ans=ans*a; return ans; }
inline Zi norm(Zi x) {
__int128 r=x.re, i=x.im;
if(r==0) return Zi(absl(i), 0);
switch((r<0)<<1|(i<0)) {
case 0: return Zi(r, i); break;
case 1: return Zi(-i, r); break;
case 2: return Zi(i, -r); break;
case 3: return Zi(-r, -i); break;
}
return Zi();
}
inline Zi gcd(Zi a, Zi b) {
while(b.re||b.im)
swap(a=norm(a%b), b);
return a;
}
inline Zi GaussPrime(ll p) {
if(p==2)
return Zi(1, 1);
if(p%4!=1)
return Zi(p, 0);
ll k=0;
while(((__int128)k*k+1)%p!=0) k=kpow(rnd(), p>>2, p);
return gcd(Zi(p, 0), Zi(k, 1));
}
inline bool Fermat(ll n,int p){
if( kpow(p,n-1,n)!=1 ) return 0;
ll k=n-1;
k>>=__builtin_ctzll(k);
ll t=kpow(p, k, n);
if(t==1) return 1;
for(;k<n-1;k<<=1, t=(__int128)t*t%n)
if(t==n-1) return 1;
return 0;
}
inline bool Miller_Rabin(ll n){
static int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 61, 233}, siz=sizeof(p)/sizeof(p[0]);
if(n==1) return 0;
for(int i=0;i<siz;++i)
if(n%p[i]==0) return n==p[i];
else if( !Fermat(n,p[i]) ) return 0;
return 1;
}
inline ll Rho(ll n,ll c){
static ll lim=128, tmp[128];
ll buf=1, tot=0;
for(ll f1=(c==n-1?0:n+1), f2=((__int128)f1*f1+c)%n; f1!=f2;
f1=((__int128)f1*f1+c)%n, f2=((__int128)f2*f2+c)%n, f2=((__int128)f2*f2+c)%n){
tmp[tot++]=f1-f2;
if(tmp[tot-1]<0) tmp[tot-1]+=n;
buf=(__int128)buf*tmp[tot-1]%n;
if(tot==lim){
if( __gcd(buf,n)>1 ) break;
tot=0;
}
}
for(int i=0;i<tot;++i){
buf=__gcd(tmp[i], n);
if(buf>1) return buf;
}
return n;
}
void Pollard_Rho(ll n, vector<pair<ll, int> > &pf, ll cnt){
static int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 61, 233}, siz=sizeof(p)/sizeof(p[0]);
if(n==1)
return ;
if( Miller_Rabin(n) ) {
pf.emplace_back(n, cnt);
return ;
}
ll d=n;
int cntd=0;
for(int i=0;i<siz;++i) if(n%p[i]==0){
d=p[i];
cntd=0;
while(n%d==0) n/=d, ++cntd;
pf.emplace_back(d, cnt*cntd);
}
while(d==n) d=Rho(n, rand()%(n-1)+1);
cntd=0;
while(n%d==0) n/=d, ++cntd;
Pollard_Rho(d, pf, cnt*cntd);
Pollard_Rho(n, pf, cnt);
}
inline ll tri2(ll a, ll b) {
if(a<=1||b==0) return 0;
return ((a%P)*(b%P)-a-b+__gcd(a, b))%P;
}
vector<pair<ll, int> > pf;
vector<Zi> tmp;
inline void solvePrime(ll n, vector<Zi> &v) {
pf.clear();
Pollard_Rho(n, pf, 1);
v.clear();
v.push_back(Zi(1, 0));
Zi q, qk, r;
for(auto &[p, k] : pf) {
k*=2;
if(p==2) {
q=kpow(Zi(1, 1), k);
for(auto &e : v)
e*=q;
continue;
}
if(p%4!=1) {
q=kpow(Zi(p, 0), k/2);
for(auto &e : v)
e*=q;
continue;
}
qk=kpow(q=GaussPrime(p), k);
r=Zi(p, 0)/q;
tmp=v;
v.clear();
v.reserve((k+1)*tmp.size());
for(int i=0; i<=k; ++i) {
for(const auto &e : tmp)
v.push_back(e*qk);
qk=qk/q*r;
}
}
for(auto &e : v)
e=norm(e);
sort(v.begin(), v.end(), [](const Zi &a, const Zi &b) {
if(a.re!=b.re) return a.re<b.re;
else return a.im<b.im;
});
int cnt=1;
for(int i=1, I=v.size(); i<I; ++i)
if(v[i].re!=v[i-1].re||v[i].im!=v[i-1].im)
v[cnt++]=v[i];
v.erase(v.begin()+cnt, v.end());
}
vector<Zi> a;
inline ll calc(ll a, ll b, ll c, ll d) {
return (tri2(a, b)+tri2(c, d)-((a-c)%P)*((b-d)%P))%P;
}
inline ll ans() {
ll n, m;
cin>>n>>m;
solvePrime(n, a);
if(n!=m) {
int siz=a.size();
a.resize(siz*2);
for(int i=0, I=siz; i<I; ++i)
a[i+siz]=a[i]*Zi(0, 1);
}
ll res=0;
Zi c;
for(auto z : a) {
c=z*Zi(0, 1);
if((__int128)c.re*m%n!=0||(__int128)c.im*m%n!=0)
continue;
c=Zi((__int128)c.re*m/n, (__int128)c.im*m/n);
res=(res+calc(absl(z.re), absl(z.im), absl(c.re), absl(c.im)))%P;
}
if(res<0) res+=P;
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T; cin>>T;
while(T--)
cout<<ans()<<"\n";
cout.flush();
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号