离散时间信号与系统的时域分析

%冲击函数
x = -10:10;
dirac(x)

%符号函数
x = -10:10;
sign(n)

%图像的平移
n = -10:10;
y = dirac(n);
y = sign(y);     %冲击函数和符号函数组合
subplot(2,1,1)
stem(n,y)      %原图像
subplot(2,1,2)
stem(n+2,y)    %向右边移动两位

t = -10:10;
t0 = 0;      %从这一点进行阶跃
y = stepfun(t,t0)  %阶跃函数
stem(t,y)

 

 

y[n]+0.75y[n-1]+0.125y[n-2]=x[n]-x[n-1]

对于上面的差分方程,利用过滤函数

n1 = 0:60;
n2 = 0:60;
f1 = 200;
f2 = 700;
%输入序列
x1 = sin(2*pi*f1*n1);
x2 = sin(2*pi*f2*n2);
%离散系统的差分方程
num = [-1 1];
denum = [1,0.75,0.125];
%输出序列
y1 = filter(num,denum,x1);
y2 = filter(num,denum,x2);
%绘制信号序列
subplot(2,2,1);
stem(n1,x2);title('输入序列x1(n)');
subplot(2,2,2);
stem(n2,x2); title('输入序列x2(n)')
subplot(2,2,3);
stem(n1,y1);title('x1(n)相应的输出序列y1(n)');
subplot(2,2,4);
stem(n2,y2);title('x2(n)相应的输出序列y2(n)');

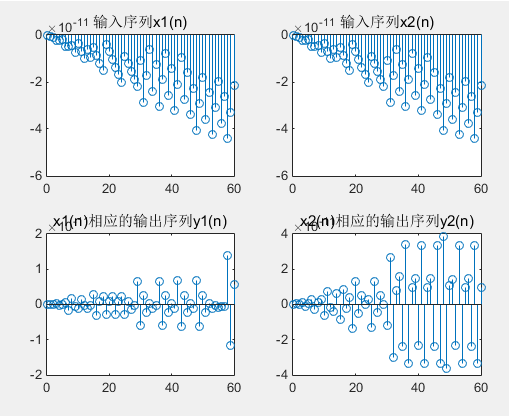
上面的是输入通过系统(filter)输出

%===输入函数
a1 = 3;
b1 = 4;
Fs = 400;
x1 = A*sin(2*pi*f1*n1/Fs);
x2 = A*sin(2*pi*f2*n2/Fs);
xn = a1*x1 + b1*x2;
%==离散系统的差分方程
num = [1 -1];
denum = [1,0.75,0.125];
%==输出序列 system
y1 = filter(num,denum,x1);
y2 = filter(num,denum,x2);
yt = a1*y1 + b1*y2;
y = filter(num,denum,xn);
%绘制信号系统
figure(3)
subplot(2,2,1);
stem(n1,x1);
title('输入序列x1(n)');
subplot(2,2,2);
stem(n2,x2);
title('输入序列x2(n)');
subplot(2,2,3);
stem(n1,y1);
title('x1(n)相应的输出序列y1');
subplot(2,2,4);
stem(n1,y2);
title('x2(n)相应的输出序列y2');
if y == yt
    disp('相等')
else
    disp('不相等')
end    

下面的是系统函数是否为线性的

 

接下来讲一讲卷积和(离散)