数据结构-树状数组(一)
复习笔记:树状数组(一)
基本原理
树状数组,顾名思义,是一个存储方式像树一样的数组。它只需要开和原数组一样大小的内存,但是每个数的位置存的并不是每个数的原始值,而是像这样:
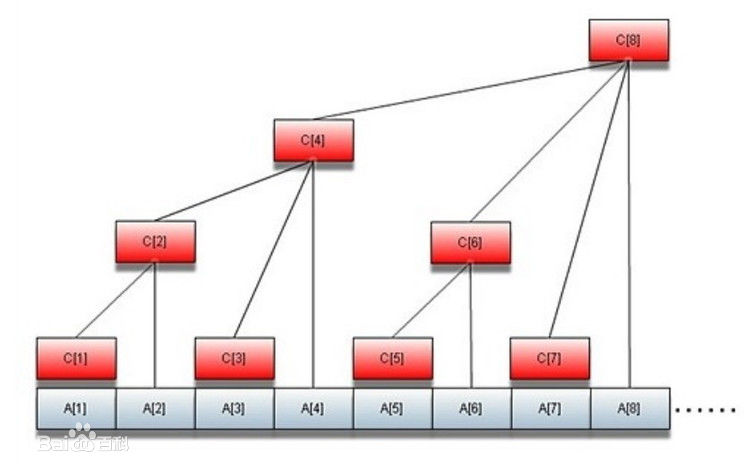 (引用自度娘)
(引用自度娘)
或者用数据来说,假设原数组为A[N],树状数组为C[N],那么存储方式就像下面这样
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这就是树状数组的存储方式。
树状数组的优势
可以很简单实现区间修改单点查询、区间查询单点修改、
例:输出数组x到y的区间和
暴力模拟:
1 int sum = 0; 2 for(int i = x;i <= y;i++) 3 sum += a[i];
很明显时间复杂度是O(n),当数据量大并且需要多次查询,难免TLE,树状数组可以解决这个问题
程序实现
性质:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax,所以很明显:Cn = A(n – 2^k + 1) + ... + An。
所以,当需要修改第x个数时,需要把所有管辖x的节点进行修改。这里就需要用到了一个很巧妙的节点转移量:Lowbit。lowbit(x)=x&(-x)。所以程序实现是这样
节点转移函数:lowbit
1 int lowbit(int x){ 2 return x&(-x); 3 }
甚至可以是这样
1 #define lowbit(x) x&-x
单点修改
在数组长度n的范围内,从x开始,每次修改完,下一个要修改的数就是当前修改数的lowbit值,这样以此类推,就可以把管辖着x的点全部修改完,也就是这样
1 void add(int x,int k){ 2 while(x <= n){ 3 tree[x] += k; 4 x += lowbit(x) 5 }
这就是把第x个点加上k的操作(tree为树状数组)
区间查询
根据树状数组的存储方式,将单点修改的程序逆过来,也就是在>=1的范围内,从x开始每次减去当前下标lowbit,并将节点权加入到总和,就可以求出A1+A2...+Ax(A为原数组值),也就是第x个数的前缀和。
1 int sum(int x) 2 { 3 int ans = 0; 4 while(x != 0) 5 { 6 ans += tree[x]; 7 x -= lowbit(x); 8 } 9 return ans; 10 }
那么想要求出x到y的区间和,只需要用Ay的前缀和减去Ax-1的前缀和即可,就像这样
1 int search(int x,int y){ 2 return sum(y) - sum(x - 1); 3 }
但大多数情况下不需要写函数,直接写到主程序里。
例题:P3374
大意:实现区间查询,单点修改
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
程序就是这样:
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cmath> 5 #include <cstring> 6 using namespace std; 7 int n,m,tree[2000010]; 8 int lowbit(int k) 9 { 10 return k & -k; 11 } 12 void add(int x,int k) 13 { 14 while(x<=n) 15 { 16 tree[x]+=k; 17 x+=lowbit(x); 18 } 19 } 20 int sum(int x) 21 { 22 int ans=0; 23 while(x!=0) 24 { 25 ans+=tree[x]; 26 x-=lowbit(x); 27 } 28 return ans; 29 } 30 int main() 31 { 32 cin>>n>>m; 33 for(int i=1;i<=n;i++) 34 { 35 int a; 36 scanf("%d",&a); 37 add(i,a); 38 } 39 for(int i=1;i<=m;i++) 40 { 41 int a,b,c; 42 scanf("%d%d%d",&a,&b,&c); 43 if(a==1) 44 add(b,c); 45 if(a==2) 46 cout<<sum(c)-sum(b-1)<<endl; 47 } 48 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号