后缀数组 + 后缀自动机小记

后缀数组 & 后缀自动机小记

基本介绍

后缀数组，英文SA，可以用于解决不少与字符串相关的题目。后缀数组本质上就是将其所有后缀进行排序得到的数组。

后缀自动机同样是一个解决字符串的强力工具，可能稍微需要一些理解，但是很板子。

后缀自动机需要较为熟练的掌握，后缀数组也最好能够掌握。

后缀自动机和后缀数组只有前缀相同 (SA,SAM)

后缀数组

定义在上文已经讲述，简单明了。大概讲一下如何求后缀数组，思想是倍增方法

朴素

暴力的方法明显是 $O(n^2 \log n)$ 的，利用倍增思想可以优化到 $O(n\log^2 n)$

性质+倍增

设两个数组，$rk_w(i)$ 和 $sa_w(i)$ 分别表示长度为 $w$ 的字符串，从第 $i$ 位开始在所有长度为 $w$ 字串中的排名，和长度为 $w$ 的字串中字典序第 $i$ 小的开始位置（若相同则按照先后位置排序）。

这里有个小的预处理，我们将字符串后面填上与之等长的0，以此解决长度不统一的问题

$rk_1,sa_1$是很容易求出来的。

我们考虑倍增，假设我们知道现在的 $rk_w,sa_w$ 会发现我们能够很容易地求出来 $sa_{2w},rk_{2w}$。

我们思考对于两个相等长度的字符串 $s,t$，其中 $s$ 字典序小于 $t$。我们将这两个串劈成两半，那么要么 $s$ 前半部分比 $t$ 小，要么前面部分相等，后面的部分 $s$ 比 $t$ 小。

把这个过程反过来，我们可以直接用两个参数 $rk_w(sa_w(i))$ 和 $rk_w(sa_w(i)+w)$ 分别作为第一关键字和第二关键字排序，这样就可以得到 $sa_{2w}$ 的值，接着反退出来 $wk_{2w}$ 即可。

附oiwiki的效果图

那我们就可以很轻易地做到 $O(n\log^2n)$ 的做法了

简单优化

这个复杂度的限制因素在于排序上面。有没有更快的排序方法？是有的。因为在 $rk$ 中每个数都在 $[1,n]$ 范围内的，因此我们可以采用基数排序，再优化掉一个 $\log$ ，可以做到$O(n\log n)$ 的优秀复杂度。

板子

/*强烈建议不要贺OIWiki的代码，因为跑得相当慢*/
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char s[1000005];
int rk[1000005],cnt[1000005],tmp[1000005];
int sa[1000005],n,M=1000,tmp2[1000005];
int main(){
    scanf("%s",s+1);
    int n=strlen(s+1);
    //presets
    for(int i=1;i<=n;i++){
        rk[i]=s[i];
        cnt[rk[i]]++;
    }
    for(int i=2;i<=M;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--)sa[cnt[rk[i]]--]=i;
    //opertation,every time *=2
    for(int T=1;T<=n;T<<=1){
        int po=0;
        for(int i=n-T+1;i<=n;++i)tmp[++po]=i;
        for(int i=1;i<=n;i++)
            if(sa[i]>T)tmp[++po]=sa[i]-T;
        //基数排序基本操作
        for(int i=1;i<=M;i++)cnt[i]=0;
        for(int i=1;i<=n;i++)cnt[rk[i]]++;
        for(int i=2;i<=M;i++)cnt[i]+=cnt[i-1];
        for(int i=n;i>=1;i--){
            sa[cnt[rk[tmp[i]]]--]=tmp[i];
            tmp[i]=0;
        }
        for(int i=1;i<=n;i++)tmp2[i]=rk[i];
        po=1;rk[sa[1]]=1;
        //倒回到rk上
        for(int i=2;i<=n;i++){	
            if(tmp2[sa[i]]==tmp2[sa[i-1]] && tmp2[sa[i]+T]==tmp2[sa[i-1]+T])rk[sa[i]]=po;
            else rk[sa[i]]=++po;
        }
        if(po==n)break;
        M=po;
    }
    for(int i=1;i<=n;i++)cout<<sa[i]<<" ";
    return 0;
}

可以详细讲一下这里面每一步的作用。

因为每一次是两个关键字的排序，采用基数排序可以大大加快排序的过程。基数排序的思路为，记录第二关键字排名第 $i$ 的对应第一关键字的位置。之后对于第二关键字从后往前扫，考察其对应的第一关键字大小关系即可，第一关键字用计数排序统计。

落实到代码中，其中 $rk,sa$ 代表意义如之前所说，$cnt$ 代表的是桶。$tmp_i$ 是代表第二关键字排行为 $i$ 的位置。每一次倍增的前面几行是处理 $tmp_i$，在 $n-T+1$ 这一部分是没有第二关键字的，因此排在最前面。从小往大考虑 $sa$ 数组，如果 $sa_i$ 即排行第 $i$ 大的前缀的位置 $>T$，那么就会有 $sa_i-T$ 的位置用其作为第二关键字，插入到序列中。

之后就是基数排序的基本操作，排序之后会得到新的 $sa$。注意到因为还没有考虑整个字符串，因此 $sa_i,sa_{i-1}$ 之间两个位置的目前考虑的后缀可能是相等的，因此在利用 $rk_{sa_i}=i$ 的性质的时候，需要提前判断是否和前一个相等。判断方式很简单，复制一份之前的 $rk$ 数组，然后检查 $(rk_{sa_i},rk_{sa_{i+w}}),(rk_{sa_{i-1}},rk_{sa_{i-1+w}})$ 毕竟就是根据这个排序的。

这下应该就能够完全看懂 SA 的代码实现了。

当然后缀数组还有一些其他的东西可以操作$^1$

后缀树

定义

后缀树就是所有后缀数组组成的 Trie 树。

小小优化

首先我们考虑简单建树，但是由于本质不同的字串的数量可能做到 $O(n^2)$ 级别$^1$ ，看起来非常不合理。

但是我们不要忘记一个很优秀的性质，就是所有叶子节点一定不会超过 $O(n)$ 个！这样意味着，有很多只有一个儿子的几点。我把这样的“棍子”合并起来，这样就可以做到了合适的后缀树。

构建后缀树

此处我们先放下不讲，为什么呢？因为后缀树用可以直接用SAM来进行构造更方便。

关于hight数组

$^1$ 这里我们讲一下 $hight$ 数组这个奇妙的东西

定义

$hight[i]=lcp(sa[i],sa[i-1])$

其中 $lcp$ 表示两个数组的最长前缀

作用

求本质不同的子串个数。

很显然，我们对于每个后缀，跳过 $higth[i]$ 个（因为很明显前面有过一样的），数一数有多少个。

我们换过来想，我们每次要跳过 $hight[i]$ 个，一个字符串总共的子串个数是 $\dfrac{n(n-1)}{2}$ 个，我们减去 $\sum hight[i]$ 即可。

求两个字串的LCP

假设两个字串 $s_1,s_2$ 它们的起始点分别是 $l_1,l_2$ 。不难发现，他们的LCP就是 $min(|s_1|,|s_2|,lcp(sa[l_1],sa[l_2]))$ ，即要么是整个串，要么是这个串开头的后缀。

接着我们求 $lcp(sa[l_1],sa[l_2])$ 会发现这恰恰是 $\min_{l1\le x \le l2}hight[x] $ 这里用各种方法维护一下即可（如线段树）。这样求 LCP 就是 $\log$ 级别的了。

构造方法

结论：$hight[rk[i]] \ge hight[rk[i-1]]-1$。

通过此结论，可以 $O(n)$ 求出来 $hight$。

int k=0;
for(int i=1,k=0;i<=n;i++){
    if(k>0)k--;
    while(s[i+k]==s[sa[rk[i]-1]+k])k++;
    ht[rk[i]]=k;
}

虽然这个性质确实感觉有点无中生有，我也没有搞明白是怎么想到的。但是是能够证明的。证明比较无聊而且没有什么意思，大概就是强行分析两者的关系。

后缀自动机（SAM）

后缀自动机和很多其他自动机一样，后缀自动机每个节点接受对于原字符串 $S$ 的所有后缀，其交集也就是 $S$ 的所有子串。在这个基础下，我们肯定要尽量满足节点数量少。

不多介绍，我们从头开始讲起。

Endpos

我们定义 $endpos(T)$ 表示一个串 $T$ 在原串所有的结束位置的集合。

如图，对于原串，$endpos(ab)=\left \{ 1,3,6 \right \}$。

我们将利用它来进行自动机的构造

parent tree

首先思考一下关于 $endpos$ 的一些性质：

如果 $x$ 是 $y$ 的一个后缀，那么 $endpos(y)$ 一定是 $endpos(x)$ 的一个子集
对于所有相等的 $endpos$（我们称之为 $endpos$ 等价类），那么其中所有的串一定是最长的那个串的后缀。

第一个性质是显然的，因为 $endpos$ 记录的就是在原串所有结束位置的集合，所以如果一个串是另一个串的后缀，那么更大的串出现的位置其一定出现过。

第二个性质根据 $endpos$ 的定义也很容易得到。

当然这两个性质都可以更为严谨地证明。

根据这两个我们会发现这是一个类似树形的结构，尝试根据包含关系构造出来树。

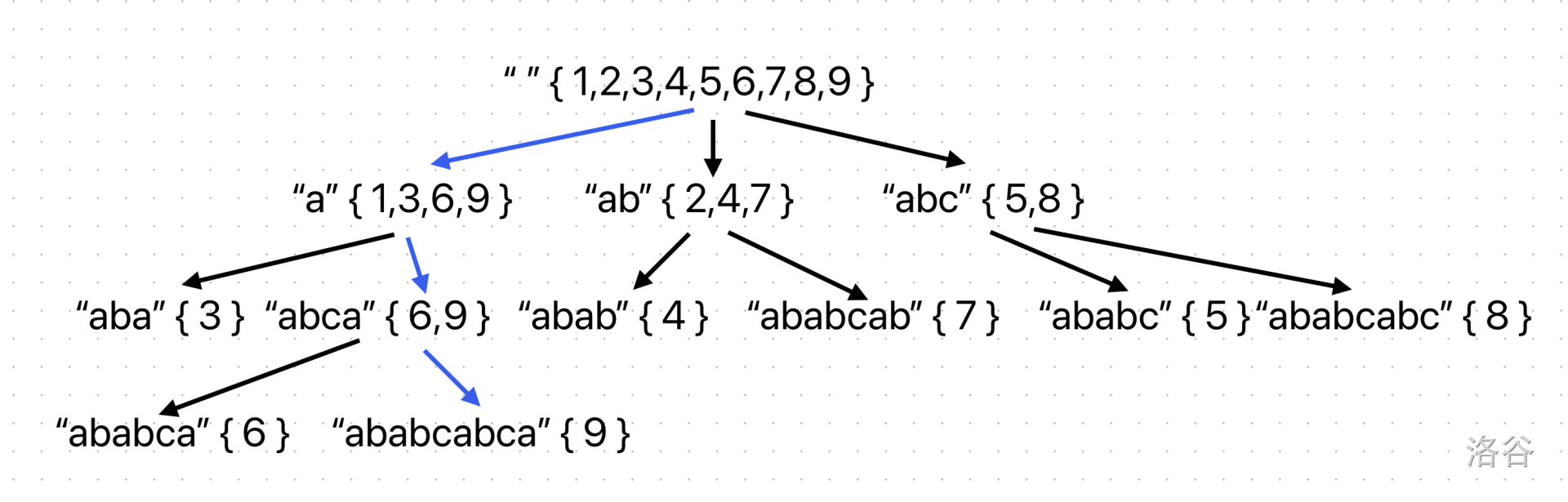
这棵树就叫做 parent tree，其节点和后缀自动机状态一一对应（注意 parent tree 并不是 SAM 真正的转移边，这个概念是不同的，只是他们的状态，即节点对应的内容是相同的）。

接下来考虑如何构造 parent tree

构造

采用动态构造的方法，对于每次新添加一个字符，考虑其所有的后缀的位置。

需要维护若干个变量：

设 $tr[u][c]$ 表示 $u$ 节点接受了 $c$ 之后转移到的点
设 $fa[u]$ 表示 parent tree 上 $u$ 的父亲
设 $len[u]$ 表示对于一个 endpos 集的最长串长度
设 $lst$ 表示当前原串所在的节点

每次加入一个新的字符 $c$，我们先新创一个节点为 $x$。我们会从 $lst$ 开始往上跳，每次经过一个节点，就会多在 SAM 上连一条边从经过的节点到 $x$。一直这样网上爬，直到找到一个点 $p$ 能够通过 $c$ 的转移到 $q$。

Case1

如果一直找不到，那么表示这是一个全新的后缀，直接 $fa[x]=0$。
Case2

如果 $len[p]+1=len[q]$ 那么表示这是一个连续的转移，也就是说对于所有 $p$ 里面的后缀，只要往后面加一个 $c$ 就能够全部丢到 $q$。此时直接 $fa[x]=tr[p][c]$ 即可。
Case3

如果 $len[p]+1\neq len[q]$ 也就说明这不是一个连续的转移，即有一部分的 $p$ 的后缀通过加一个 $c$ 并不是都能够丢到 $q$ 里面。此时要考虑分裂。

我们复制一个 $q$ 出来，设 $nq$。对于 $nq$，它首先要继承所有 $q$ 的信息，唯一不同的是，我们要设 $len[nq]=len[p]+1$ 即强制让其能够转移。之后从 $p$ 开始往上爬，每一个点只要有连向 $q$ 都让其连向 $nq$。这样就劈开了两个部分，最后让 $fa[nq]=fa[x]=nq$。就成功进行了劈开。

记得最后 $lst=x$。

void ins(int c){
    int x=++cnode,p=lst;
    lst=cnode;
    w[cnode]=1;
    len[x]=len[p]+1;
    for(;p&&!tr[p][c];p=fa[p])tr[p][c]=x;
    if(!p)fa[x]=1;//Case 1
    else{
        int q=tr[p][c];
        if(len[q]==len[p]+1)fa[x]=q;//Case 2
        else{
            int newn=++cnode;//Case 3:clone
            for(int i=0;i<=25;i++)tr[newn][i]=tr[q][i];
            fa[newn]=fa[q];
            len[newn]=len[p]+1;
            fa[q]=fa[x]=newn;
            for(;p&&tr[p][c]==q;p=fa[p])tr[p][c]=newn;//reset
        }
    }
}

后缀自动机的主要部分也就讲完了，但是没有讲性质，因为需要结合具体的题目。

posted @ 2023-02-04 17:04 Jryno1 阅读(44) 评论(0) 收藏举报来源

刷新页面返回顶部

Loading

Jryno1's blog