LCT小记

UPD

2023.7.26 更新（其实是复习了一下），改变了一些之前的格式和部分内容，添加代码 + 练习。

基本介绍

LCT 是一种数据结构，可以来解决动态树的问题，思路和树链剖分相似，都是将树分成若干条链解决问题。比树剖 + 线段树其实是少一个 $\log$ 的，但是常数较大，整体代码其实没有树剖 + 线段树长，而且除了 splay 和 roatate 其他函数都是几行的。（感觉 J 大佬挺支持使用 LCT 而不是树剖 + 线段树）当然，Toptree 就是类似于把这两者合在一起，但是 J 大佬亲自说实用性不强。

功能比较多，但是也有一定的局限性，如关于子树的操作一定要可减的，之后练习应该会讲到。

不必感到很恐惧，慢慢也就熟了。

前置芝士

Splay

Splay 是 LCT 的基础，之前也没有写过相关的内容，这里就一并介绍了。

虽然 LCT 和 Splay 的细节不太一样，但是仍然需要知道 Splay 的思想。

旋转操作（Rotate）

Splay 里面的核心，本质就是不改变中序遍历的情况下让树的层数减小（当然仍然满足二叉搜索树的性质）。

形象一点就是这样的：

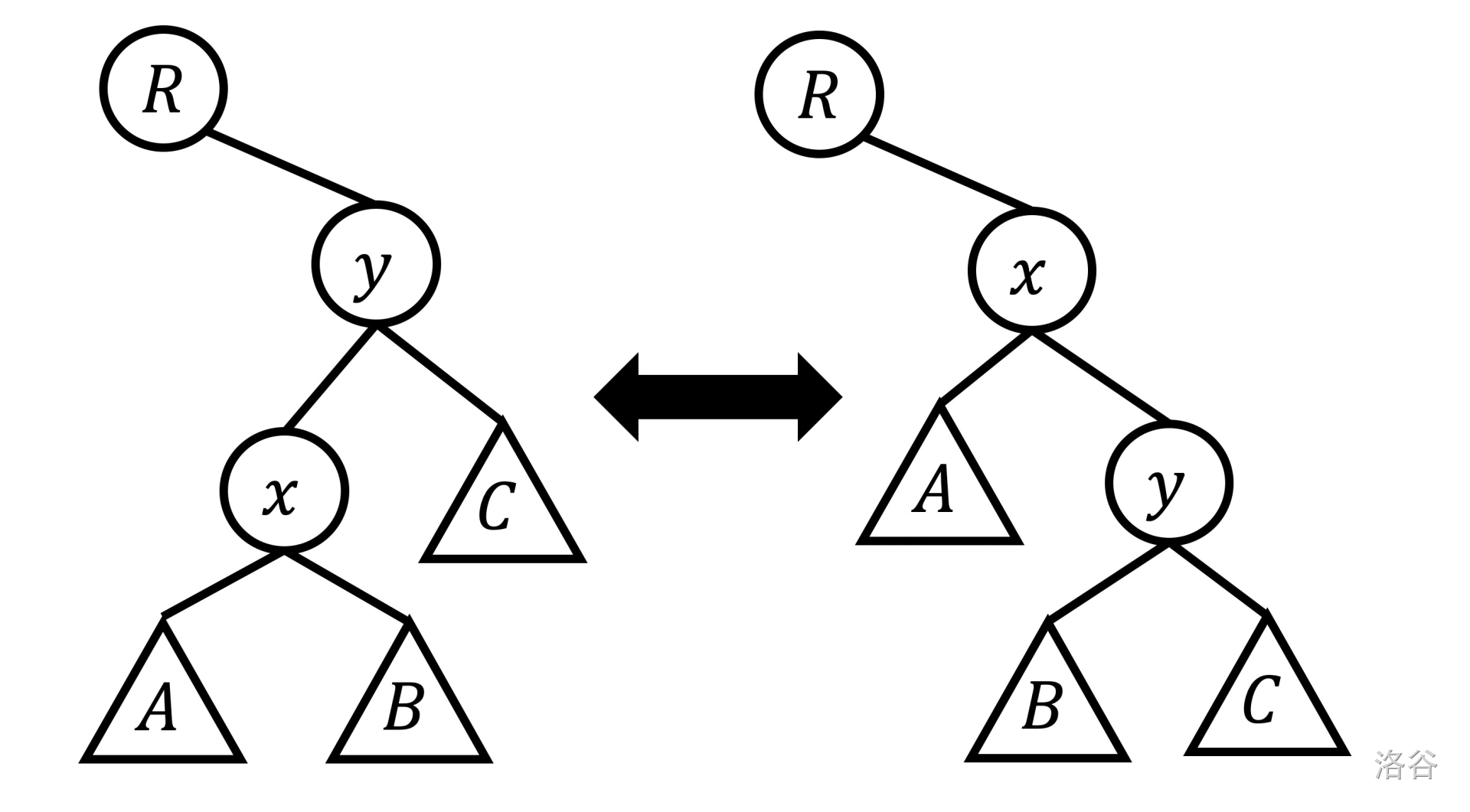
图中就是把 $x$ 节点旋转上去了。

rotate 只需要理解是哪个子树挂到哪里就可以了。（我甚至好像没有一个纯净的代码）。

Splay 操作

Splay 操作的实际效果，就是将 $x$ 节点旋转到根节点，方便进行别的操作。

第一反应就是对着 $x$ 一顿旋转，知道到了根节点的位置。这样的操作是可行的，但是并不是最优的方法，也就是说容易被卡（具体证明非常复杂，比较简单的说法是画一条长链就会发现区别），我们用“双旋”的方法优化一下。

一下 $R$ 表示根节点。

具体分类讨论：

如果 $x$ 的父亲就是 $R$：直接旋转。
如果 $x$ 的父亲和 $x$ 的祖父在同一侧：先旋转 $x$ 的父亲，再旋转 $x$。
如果 $x$ 的父亲和 $x$ 的祖父不在同一侧：旋转两次 $x$。

能够实现的操作

Splay 实现各种操作的详细内容就不再讲了，主要有插入、找前驱后继、查询第 k 个数、删除。

实链剖分

LCT 使用的是实链剖分，然后用 Splay 来维护，可以类比为重链剖分和线段树维护。

实边是正常的 Splay 储存方法，而虚边是一个 Splay 的根节点的 fa 指针指向的一个 Splay 的节点，而这个节点的儿子没有这个根节点。

听起来很抽象吧？先这样理解一下，实边其实就是一条双向边，儿子和父亲都彼此认识。而虚边是一条单向边，只有儿子认识父亲，而且这个儿子一定是一个 Splay 的根节点。

这样，给我们一个正常的树，我们通过了实链剖分，接着用若干个 Splay 树，通过虚实边的连接，就可以构造出来一个辅助树

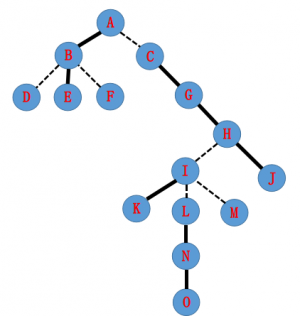
形象一点我们可以看两个图

（注：这个图是网上比较流行的图，所以就直接借鉴）

这是原树：

这是一个可能（形态是不唯一的）的辅助树：

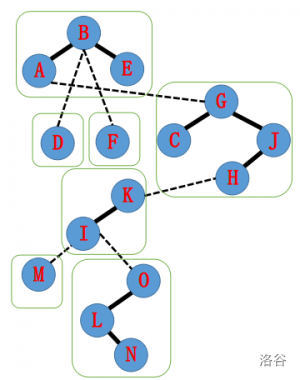
简单性质

因为 Splay 维护的一条实链，所以有性质：

所有节点存在且仅存在于一个Splay当中
每个 Splay 中的节点深度按照中序遍历的顺序递增

具体操作

Access操作

效果：

Access 操作就是将原树上的根到 $x$ 的路径在辅助树上变成实链。

步骤

把当前节点 splay 到根
把当前节点的右儿子（根据性质 $2$ 知道肯定是右儿子）替换为上一个节点（如果是第一次则为 $0$）
对当前节点的父亲进行同样的操作

可能有点抽象，我们用图来解释。

假设我们对于上面的那个树的 $N$ 节点进行 Access 操作。

首先我们找到 $N$ 并且 Splay，之后将 $N$ 的右儿子设为 $0$（也就是将右儿子抛弃掉）。

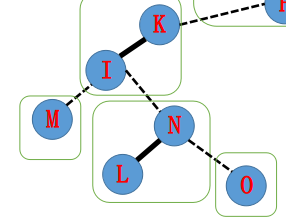
操作1.png

接着我们对 $N$ 现在的父亲进行同样的操作，将 $I$ Splay 并且将右儿子设为 $N$。

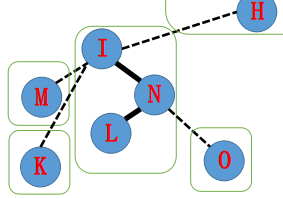
操作2.png

接着对于 $H$ 进行操作，同理。

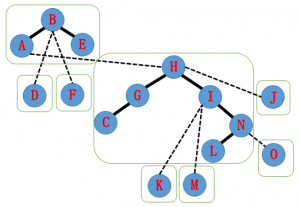
操作3.png

最后对于 $A$ 操作，得到最终的图像：

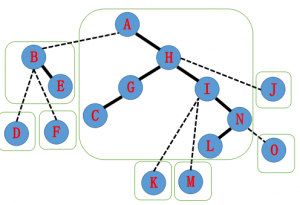
操作4_结束.png

将这样一个辅助树还原成原树，其根和 $N$ 就会有一条实链相连着。

void access(int x){
   for(int y=0;x;x=fa[y=x]){
      splay(x);
      ch[x][1]=y;
      PU(x);
   }
}

其中的最后一句话是 pushup 即上传信息，具体看题目要求什么。

Makeroot操作

效果

Makeroot 是给原树换根为 $x$

步骤

$access(x)$
$splay(x)$
翻转 Splay

什么叫做翻转 Splay 呢，我们想一下，同样对于 $N$，我们换根就是要把这个 access 之后的中序遍历给反过来。也就是 $ACGHILN$ 变成 $NLIHGCA$ 这样子。

那么我们翻转其实就只需要把每一个节点的右儿子和左儿子互换一下就可以了。

void PR(int x){
   swap(ch[x][0],ch[x][1]);
   laz[x]^=1;
}
void PD(int x){
   if(laz[x]){
      PR(ch[x][0]),PR(ch[x][1]);
      laz[x]=0; 
   }
}
void MR(int x){
   access(x),splay(x);
   PR(x);
}

其中会打一个懒标记，减少操作数量，和线段树一样。

Findroot操作

效果

找到 $x$ 在原树中的根节点

步骤

$access(x)$
$splay(x)$
找到 $x$ 所在 splay 最左边的仁兄，这就是$x$在原树中的根节点
为了防止卡链，需要再次 splay 一下仁兄

这里理解很好，就是中序遍历的第一个位置

最后为了防止卡链就是为了避免一个很长的链，然后一直对最上面的节点 findroot。

int FR(int x){
   access(x),splay(x);
   while(ch[x][0])x=ch[x][0];
   splay(x);
   return x;
}

Link操作

效果

字面意思，就是连边

步骤

$makeroot(x)$
如果 $findroot(y)$，说明 $x$ 和 $y$ 已经在同一棵树上了，就是不合法的
把 $x$ 的父亲设置为 $y$ 连一条虚边

void link(int x,int y){
   MR(x);
   if(FR(y)!=x)fa[x]=y;
}

Cut操作

效果

字面意思，断掉边

步骤

$makeroot(x)$
判断合法性
1. $findroot(y)$ 检查是否是 $x$，注意 findroot 最后一个操作会保证 $x$ 一定是根节点了，这对于第二部判断是一个铺垫
2. 判断 $x,y$ 是否相邻，具体就是 $y$ 的父亲不是 $x$ 或者 $y$ 有左儿子
断边（$y$ 的父亲 $x$ 的儿子）
更新

void cut(int x,int y){
   MR(x);
   if(FR(y)==x&&fa[y]==x&&!ch[y][0]){
      fa[y]=ch[x][1]=0;
      PU(x);
   }
}

Split操作

效果

把$x,y$的路径拆成一棵方便操作的splay出来

步骤

$makeroot(x)$
$access(y)$
$splay(y)$

void split(int x,int y){
   MR(x);
   access(y),splay(y);
}

具体维护

与题目本身相关，先不在这里说。

题目

P3690

简单模板，对于每个点记录在辅助树上面其左右儿子和自己的异或和，在询问的时候直接将 $x$ 定做根，之后把 $y$ 拉到 Splay 的根上输出其值即可。

后面两个操作都是板子里面可以处理的。

#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+5;
int ch[maxn][2],fa[maxn],siz[maxn],a[maxn],w[maxn],laz[maxn];
int n,m;
inline bool notroot(int x){
   return ch[fa[x]][0]==x||ch[fa[x]][1]==x;
}
void PU(int x){
   w[x]=w[ch[x][0]]^w[ch[x][1]]^a[x];
}
void PR(int x){
   swap(ch[x][0],ch[x][1]);
   laz[x]^=1;
}
void PD(int x){
   if(laz[x]){
      PR(ch[x][0]),PR(ch[x][1]);
      laz[x]=0; 
   }
}
void rotate(int x){
   int y=fa[x],z=fa[y],k=(ch[y][1]==x),ot=ch[x][!k];
   if(notroot(y))ch[z][ch[z][1]==y]=x;
   ch[x][!k]=y,ch[y][k]=ot;
   if(ot)fa[ot]=y;
   fa[y]=x,fa[x]=z;
   PU(y);
}
void UPD(int x){
   if(notroot(x))UPD(fa[x]);
   PD(x);
}
void splay(int x){
   UPD(x);
   while(notroot(x)){
      int y=fa[x],z=fa[y];
      if(notroot(y))rotate((x==ch[y][1])^(y==ch[z][1])?x:y);
      rotate(x);
   }
   PU(x);
}
void access(int x){
   for(int y=0;x;x=fa[y=x]){
      splay(x);
      ch[x][1]=y;
      PU(x);
   }
}
int FR(int x){
   access(x),splay(x);
   while(ch[x][0])PD(x),x=ch[x][0];
   splay(x);
   return x;
}
void MR(int x){
   access(x),splay(x);
   PR(x);
}
void split(int x,int y){
   MR(x);
   access(y),splay(y);
}
void link(int x,int y){
   MR(x);
   if(FR(y)!=x)fa[x]=y;
}
void cut(int x,int y){
   MR(x);
   if(FR(y)==x&&fa[y]==x&&!ch[y][0]){
      fa[y]=ch[x][1]=0;
      PU(x);
   }
}
int main(){
   cin>>n>>m;
   for(int i=1;i<=n;i++)scanf("%d",&a[i]);
   while(m--){
      int opt,x,y;
      scanf("%d%d%d",&opt,&x,&y);
      if(opt==0)split(x,y),cout<<w[y]<<"\n";
      if(opt==1)link(x,y);
      if(opt==2)cut(x,y);
      if(opt==3)splay(x),a[x]=y;
   }
   return 0;
}

P1501

和线段树一样，对于区间加和区间乘对于一个点打上 lazytag 就好，注意加法和乘法的顺序问题。维护路径和同理，其实也是挺板子的。这里就放一下有改变的一些操作。

//s->sum,lazs->sum lazytag,lazp->product lazytag,lazr->rotate lazytag
inline void PU(int x){
   s[x]=(s[ch[x][0]]+s[ch[x][1]]+a[x])%mod;
   siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;
}
inline void Pushr(int x){
   swap(ch[x][0],ch[x][1]);
   lazr[x]^=1;
}
inline void Pusha(int x,int c){//push add
   s[x]=(s[x]+1ll*c*siz[x]%mod)%mod;
   a[x]=(a[x]+1ll*c)%mod;
   lazs[x]=(lazs[x]+1ll*c)%mod;
}
inline void Pushm(int x,int c){
   s[x]=s[x]*1ll*c%mod;
   a[x]=a[x]*1ll*c%mod;
   lazp[x]=lazp[x]*1ll*c%mod;
   lazs[x]=lazs[x]*1ll*c%mod;//(a+b)*c=a*c+b*c
}
inline void PD(int x){
   if(lazp[x]!=1){//order
      if(ch[x][0])Pushm(ch[x][0],lazp[x]);
      if(ch[x][1])Pushm(ch[x][1],lazp[x]);
      lazp[x]=1;
   }
   if(lazs[x]){
      if(ch[x][0])Pusha(ch[x][0],lazs[x]);
      if(ch[x][1])Pusha(ch[x][1],lazs[x]);
      lazs[x]=0;
   }
   if(lazr[x]){
      if(ch[x][0])Pushr(ch[x][0]);
      if(ch[x][1])Pushr(ch[x][1]);
      lazr[x]=0;
   }
}

P2542

这里就涉及到一些小技巧（题目的转化）了。

考虑如何维护关键航线的数量，删边不好做，但是反过来加边是可以考虑的。如果一条边连接了两个之前没有连接的连通块，那么其一定是一条关键航线，反之，它会让它连接的两个点上所有的路径上的边都变为不关键的。

而两个点之间关键边之间的数量可以简单的用路径求和即可。

这样就变成一个两个操作：

每次加一条路径权值为 $1$ 的边
每次路径修改为 $0$
查询两个点之间的路径权值和

由于 LCT 只能维护点权，我们不妨把一条路径化为一个点，设 $(u,v)$ 对应的点是 $id+n$，那么每次连边连接 $(u,id+n),(v,id+n)$ 即可。

对于路径修改，我们可以拉出来那一条链，之后打上一个标记，表示这些所有路径的值都应该是 $0$。

void PU(int x){
   w[x]=w[ls]+w[rs]+a[x];
}
void PD(int x){
   if(laz[x]){
      if(ls)w[ls]=a[ls]=0,laz[ls]=1;
      if(rs)w[rs]=a[rs]=0,laz[rs]=1;
      w[x]=laz[x]=0;
   }
   if(lazr[x]){
      if(ls)PR(ls);
      if(rs)PR(rs);
      lazr[x]=0;
   }
}

int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>ed[i].u>>ed[i].v;
        if(ed[i].v<ed[i].u)swap(ed[i].v,ed[i].u);
        mk[make_pair(ed[i].u,ed[i].v)]=i+n;
        T.a[i+n]=1;
    }
    while(1){
        int op;
        Q now;
        cin>>op;
        if(op==-1)break;
        now.opt=op;
        cin>>now.u>>now.v;
        if(now.v<now.u)swap(now.u,now.v);
        if(op==0)mp[make_pair(now.u,now.v)]=1;
        q.push_back(now);
    }
    reverse(q.begin(),q.end());
    for(int i=1;i<=m;i++){
        int val=mk[make_pair(ed[i].u,ed[i].v)];
        if(!mp[make_pair(ed[i].u,ed[i].v)]){
            T.MR(ed[i].u);
            if(T.FR(ed[i].v)!=ed[i].u){
                T.link(ed[i].u,val),T.link(val,ed[i].v);
            } else {
                T.split(ed[i].u,ed[i].v);
                T.a[ed[i].v]=T.w[ed[i].v]=0,T.laz[ed[i].v]=1;
            }
        }
    }
    for(int i=0;i<q.size();i++){
        if(q[i].opt==1){
            T.split(q[i].u,q[i].v);
            ans.push_back(T.w[q[i].v]);
        } else {
            int val=mk[make_pair(q[i].u,q[i].v)];
            T.MR(q[i].u);
            if(T.FR(q[i].v)!=q[i].u){
                T.link(q[i].u,val),T.link(val,q[i].v);
            } else {
                T.split(q[i].u,q[i].v);
                T.a[q[i].v]=T.w[q[i].v]=0,T.laz[q[i].v]=1;
            }
        }
    }
    reverse(ans.begin(),ans.end());
    for(int i=0;i<ans.size();i++){
        cout<<ans[i]<<"\n";
    }
    return 0;
}

HDOJ 7300

这里涉及到 LCT 另一个用法，维护生成树。

首先化题目，这个限制非常奇怪，但是我们发现有必要条件是 $w$ 一定要大于等于最小生成树的 $k$ 小边，小于等于最大生成树的 $k$ 小边。

这个是否是充分的？经过证明会发现是的（证明暂略）。

LCT 有功能可以来维护动态最小生成树，每次添加一条边的时候，如果连接了两个本来不连通的连通块那么可以直接连，否则考虑连接的两个点的路径上的所有边的最大的边，如果这条边的权值比最大的边的权值小那么可以替换之，否则直接扔掉。

关于如何维护边和上一题一样。

对于第 $k$ 小我直接用的权值线段树维护的（其实树状数组会简单很多）。

void PU(int x){
   maxx[x]=x,minn[x]=x;
   if(ls&&w1[maxx[ls]]>w1[maxx[x]])maxx[x]=maxx[ls];
   if(rs&&w1[maxx[rs]]>w1[maxx[x]])maxx[x]=maxx[rs];
   if(ls&&w2[minn[ls]]<w2[minn[x]])minn[x]=minn[ls];
   if(rs&&w2[minn[rs]]<w2[minn[x]])minn[x]=minn[rs];
}

/*lb->LCT Big;ls->LCT Small;sb->SGT Big;ss->SGT small*/
//比较尴尬的是，写的过程中lb和ls写反了。也不想再改了，但是能理解在干啥就好
while(T--){
   cin>>n>>q;
   init();
   for(int i=1;i<=q;i++){
      int opt;
      cin>>opt;
      if(opt==1){
            int u,v,w;
            cin>>u>>v>>w;
            ap[w]=1;
            lb.w1[i+n]=lb.w2[i+n]=ls.w1[i+n]=ls.w2[i+n]=w;
            lb.MR(u),ls.MR(u);
            if(u!=lb.FR(v)){
               cnt++;
               lb.link(i+n,u),lb.link(i+n,v);
               sb.CT(1,1,q,w,1);

            } else {
               lb.split(u,v);
               int tmp=lb.maxx[v];
               if(w<lb.w1[tmp]){
                  lb.splay(tmp);
                  lb.fa[lb.ch[tmp][0]]=lb.fa[lb.ch[tmp][1]]=0;
                  lb.link(i+n,u),lb.link(i+n,v);
                  sb.CT(1,1,q,lb.w1[tmp],-1); 
                  sb.CT(1,1,q,w,1);
               }
            }
            if(u!=ls.FR(v)){
               ls.link(i+n,u),ls.link(i+n,v);
               ss.CT(1,1,q,w,1);
            } else {
               ls.split(u,v);
               int tmp=ls.minn[v];
               if(w>ls.w2[tmp]){
                  ls.splay(tmp);
                  ls.fa[ls.ch[tmp][0]]=ls.fa[ls.ch[tmp][1]]=0;
                  ls.link(i+n,u),ls.link(i+n,v);
                  ss.CT(1,1,q,ls.w2[tmp],-1);
                  ss.CT(1,1,q,w,1);
               }
            }
      } else {
            int k,w;
            cin>>k>>w;
            int small=sb.QT(1,1,q,k),big=ss.QT(1,1,q,k);
            if(ap[w]&&cnt==n-1&&w>=small&&w<=big){
               cout<<"YES"<<"\n";
            } else {
               cout<<"NO"<<"\n";
            }
      }
   }
}

有点长，但是封装起来还好，而且要维护最大和最小，所以多了一半的代码。

这些例题应该能够理解 LCT 的用法了，目前 LCT 的一些基础内容应该算比较完善了，以后如果有更进一步的东西可能会继续补充，一步一步来。

LCT 小记基础这个小坑算是填完了。

posted @ 2023-07-08 10:43 Jryno1 阅读(24) 评论(0) 收藏举报来源

刷新页面返回顶部

Loading

Jryno1's blog

LCT小记

LCT小记

UPD

基本介绍

前置芝士

Splay

旋转操作（Rotate）

Splay 操作

能够实现的操作

实链剖分

简单性质

具体操作

Access操作

效果：

步骤

Makeroot操作

效果

步骤

Findroot操作

效果

步骤

Link操作

效果

步骤

Cut操作

效果

步骤

Split操作

效果

步骤

具体维护

题目

P3690

P1501

P2542

HDOJ 7300

公告