【深度学习】|01复旦大学邱锡鹏《神经网络与深度学习》学习小笔记（四）优化正则

优化与正则

　　网络优化难点，改善方法

一、优化与正则

优化：经验风险最小

正则化：降低模型复杂度

---

 

（1）网络优化

a.网络优化难点：

　　结构差异大
　　　　没有通用的优化算法
　　　　超参数多

　　非凸优化问题
　　　　参数初始化
　　　　逃离局部最优（鞍点）

　　梯度消失（爆炸）问题

b.神经网络优化的改善方法：

更有效的优化算法来提高优化方法的效率和稳定性
　　动态学习率调整
　　梯度估计修正
更好的参数初始化方法、数据预处理方法来提高优化效率
修改网络结构来得到更好的优化地形
　　优化地形（ Optimization Landscape ）指在高维空间中损失函数的曲面形状
　　好的优化地形通常比较平滑
　　使用 ReLU 激活函数、残差连接、逐层归一化等
使用更好的超参数优化方法

c.Batchsize和learning rate

批量越大，随机梯度的方差越小，引入的噪声也越小，训练也越稳定，因此可以设置较大的学习率．
而批量较小时，需要设置较小的学习率，否则模型会不收敛．

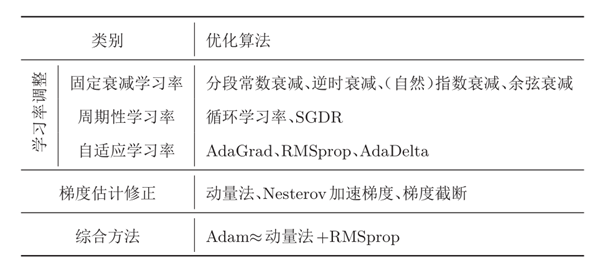
d.优化算法 wt = wt-lr*m/sqirt(V)

自己整理的一些资料：
链接

更多：知乎

帮助记忆一部分：

元素：梯度，一阶动量m，二阶动量V

SGD（一阶动量）

SGDM（加在一阶动量上的momentum）

　　m_w = beta*m_w+(1-beta)*grads[0]

Adagrad（一阶gradient，累加的二阶动量）

RMSprop（一阶gradient，momentum的二阶动量）

AdaDelta在RMSprop的基础上多维护了一个学习率

adam(给Adagrad的两个都加momentum)

e.梯度截断

梯度截断是一种比较简单的启发式方法，把梯度的模限定在一个区间，当梯度的模小于或大于这个区间时就进行截断。

f.参数初始化

　　1.预训练初始化
　　2.随机初始化

　　　　Gaussian初始化方法是最简单的初始化方法，参数从一个固定均值（比如0）和固定方差（比如0.01）的Gaussian分布进行随机初始化。

　　　　均匀分布初始化：参数可以在区间[−r,r]内采用均匀分布进行初始化。

　　　　基于方差缩放的参数初始化

　　　　正交初始化
　　　　　　1 ）用均值为 0 、方差为 1 的高斯分布初始化一个矩阵；
　　　　　　2 ）将这个矩阵用奇异值分解得到两个正交矩阵，并使用其中之一作为权重矩阵。

　　3.固定值初始化
　　　　偏置（ Bias ）通常用 0 来初始化

g.归一化方法
　　批量归一化（Batch Normalization，BN）
　　层归一化（Layer Normalization）
　　权重归一化（Weight Normalization）
　　局部响应归一化（Local Response Normalization，LRN）

h.超参数优化

　　网格搜索: 𝑚_1  × 𝑚_2 ×···× 𝑚_𝐾 个取值组合

　　随机搜索: 随机搜索

　　贝叶斯优化
　　动态资源分配
　　神经架构搜索

i.Dropout :就是集成学习，bagging的一种策略

 　　对于一个神经层𝑦 = 𝑓(𝑊𝑥+𝑏)，引入一个丢弃函数𝑑(·)使得𝑦 = 𝑓(𝑊𝑑(𝑥)+𝑏)。

　　　　

 　　其中𝑚 ∈ 〖{0,1}〗^𝑑  是丢弃掩码（dropout mask），通过以概率为p的贝努力分布随机生成

 NLP方向暂时就整理到这里吧^.^后续会把Self-Attention,Transformer,BERT放在一起整理