【核心算法8】最短路径问题
手机导航是怎么得出两个地点间的最短线路?把地图简化为一个加权图,然后利用这个加权图查找最短路径。
将地点看成节点,把道路看成边,整个地图就可看成一个加权图
- 迪克斯特朗算法(Dijkstra算法)
- 弗洛伊德算法(Floyd算法)
- A*算法
迪克斯特朗算法
如图所示公交车线路图,从A站到F站,如何知道坐车距离最短,可用迪克斯特朗算法。
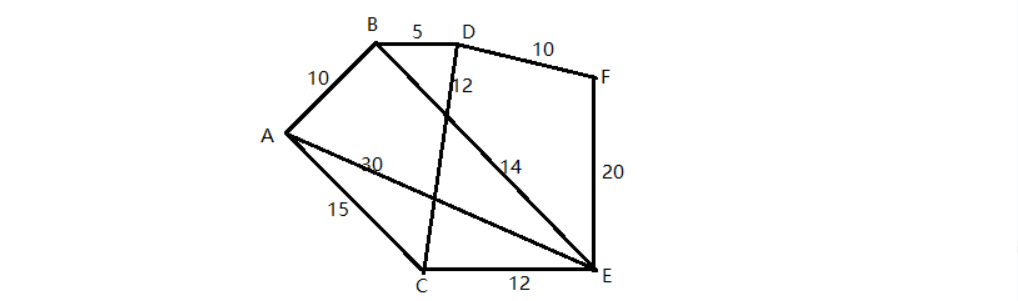
迪克斯特朗算法,又被译为戴克斯特拉算法,它主要用于解决有向图的最短路径问题。
输入边的权重和一个起点,迪克斯特朗算法能够得出从该起点到任何其他节点的最短路径。
(权重不可为负)
术语解释
| 术语 | 解释 |
|---|---|
| 图 | 一个图是由节点和连接这些节点的边组成 |
| 节点 | 一个小圆点,可以看成一个事物,站点,城市等 |
| 边 | 连接节点的直线和曲线 |
| 有向图 | 赋予边方向的图 |
| 权重 | 边的距离 |
| 前任节点 | 路线中连接节点的上一个节点 |
问题描述
观察这个公交车系统包括6个站点和连接车站的9条边。图中每条边上都标有距离,也就是权重。另外,每条边都是双向的,可以从一个车站到另一个车站,也可以从那一个车站回到这个车站。
迪克斯特朗算法的基本概念是,如果设定一个车站为起点,那么算法能够找出一个公交车系统中从该车站到任意车站的最短距离路线。主要特点是以起点为中心向外层层扩展,直到扩展到终点为止
思路解析
-
图的定义
class Graph(object): def __init__(self): # 节点集合 self.nodes = set() # 存储边集合的字典 self.edges = dict() # 记录每条边的距离的集合 self.distances = {} def add_node(self, node): """ 增加节点 :param node: :return: """ self.nodes.add(node) def add_edge(self, from_node, to_node, distance): """ 增加边 :param from_node: 起点 :param to_node: 终点 :param distance: 距离 :return: """ if from_node not in self.edges.keys(): self.edges[from_node] = [to_node] else: self.edges[from_node].append(to_node) self.distances[(from_node, to_node)] = distance -
节点的定义
class Node(object): def __init__(self, name): """ :param name: 节点名称 """ # 设定起始距离值为最大值 self.distance = sys.maxsize # 起始节点的前任节点为空 self.predecessor = None self.name = name # 设定距离值 def set_distance(self, dist): self.distance = dist # 设定前任节点 def set_predecessor(self, pred): self.predecessor = pred # 获取距离值 def get_distance(self): return self.distance # 获取前任节点 def get_predecessor(self): return self.predecessor -
用代码将图实现
g = Graph() g.add_node(Node('A')) g.add_node(Node('B')) g.add_node(Node('C')) g.add_node(Node('D')) g.add_node(Node('E')) g.add_node(Node('F')) g.add_edge('A', 'B', 10) g.add_edge('B', 'A', 10) g.add_edge('A', 'C', 15) g.add_edge('C', 'A', 15) ... g.add_edge('E', 'F', 20) g.add_edge('F', 'E', 20) -
算法核心1:两个节点集合
定义连个节点集合:临时节点集合和永久节点集合
- 临时节点集合:存储距离值和改变空间节点
- 永久节点集合:存储距离值已经固定的节点
permanent = set() temporary = set() # 算法开始把起始点加入临时节点集合 temporary.add(initial) -
算法核心2:循环
一直循环两个步骤,它每循环一次都要确保局部最优
- 找到临时节点集合中距离值最小的节点,把它迁移到永久集合中
- 检查该节点的相邻节点集合,若相邻节点不属于永久集合,则尝试更新其距离值,一旦更新成功便吧该相邻节点加入临时节点集合
-
输出路线
从终点回溯到起点就可以得到最短路线
代码实现
import sys
from collections import defaultdict
class Graph(object):
def __init__(self):
# 节点集合
self.nodes = {}
# 存储边集合的字典
self.edges = defaultdict(list)
# 记录每条边的距离的集合
self.distances = {}
def add_node(self, node):
"""
增加节点
:param node:
:return:
"""
self.nodes.setdefault(node.name, node)
def add_edge(self, from_node, to_node, distance):
"""
增加边
:param from_node: 起点
:param to_node: 终点
:param distance: 距离
:return:
"""
# if from_node not in self.edges.keys():
# self.edges[from_node] = [to_node]
# else:
self.edges[from_node].append(to_node)
self.distances[(from_node, to_node)] = distance
def print_path(self, end):
current = end
path = [end]
while self.nodes[current].get_predecessor() != None:
path.append(self.nodes[current].get_predecessor().name)
current = self.nodes[current].get_predecessor().name
path.reverse()
print(path)
def dijkstra(self, initial, end):
permanent = set()
temporary = set()
temporary.add(initial)
self.nodes[initial].set_distance(0)
while temporary:
min_node = None
for node in temporary:
if min_node is None:
min_node = self.nodes[node]
elif self.nodes[node].get_distance() < min_node.get_distance():
min_node = self.nodes[node]
temporary.remove(min_node.name)
permanent.add(min_node.name)
current_distance = min_node.get_distance()
for neighbour in self.edges[min_node.name]:
new_distance = current_distance + self.distances[(min_node.name, neighbour)]
if neighbour not in permanent and new_distance < self.nodes[neighbour].get_distance():
self.nodes[neighbour].set_distance(new_distance)
self.nodes[neighbour].set_predecessor(min_node)
temporary.add(neighbour)
self.print_path(end)
class Node(object):
def __init__(self, name):
"""
:param name: 节点名称
"""
self.name = name
# 起始节点的前任节点为空
self.predecessor = None
# 设定起始距离值为最大值
self.distance = sys.maxsize
# 设定距离值
def set_distance(self, dist):
self.distance = dist
# 设定前任节点
def set_predecessor(self, pred):
self.predecessor = pred
# 获取距离值
def get_distance(self):
return self.distance
# 获取前任节点
def get_predecessor(self):
return self.predecessor
if __name__ == '__main__':
solution1 = 'C'
solution2 = 'F'
g = Graph()
a = Node('A')
b = Node('B')
c = Node('C')
d = Node('D')
e = Node('E')
f = Node('F')
g.add_node(a)
g.add_node(b)
g.add_node(c)
g.add_node(d)
g.add_node(e)
g.add_node(f)
g.add_edge('A', 'B', 10)
g.add_edge('B', 'A', 10)
g.add_edge('A', 'C', 15)
g.add_edge('C', 'A', 15)
g.add_edge("A", "E", 30)
g.add_edge("E", "A", 30)
g.add_edge("B", "E", 14)
g.add_edge("E", "B", 14)
g.add_edge("B", "D", 5)
g.add_edge("D", "B", 5)
g.add_edge("C", "E", 12)
g.add_edge("E", "C", 12)
g.add_edge("C", "D", 12)
g.add_edge("D", "C", 12)
g.add_edge("D", "F", 10)
g.add_edge("F", "D", 10)
g.add_edge('E', 'F', 20)
g.add_edge('F', 'E', 20)
g.dijkstra(solution1, solution2)
# >>>
# ['C', 'D', 'F']
弗洛伊德算法
Floyd算法和迪克斯特朗算法一样,可用于解决加权图的最短路径问题。
迪克斯特朗算法要求权重不为负数,Flody算法没有这项规则
问题描述
继迪克斯特朗算法解决的公交车线路距离最近问题,用Floyd算法解决
(将原来A-F用0-5表示)
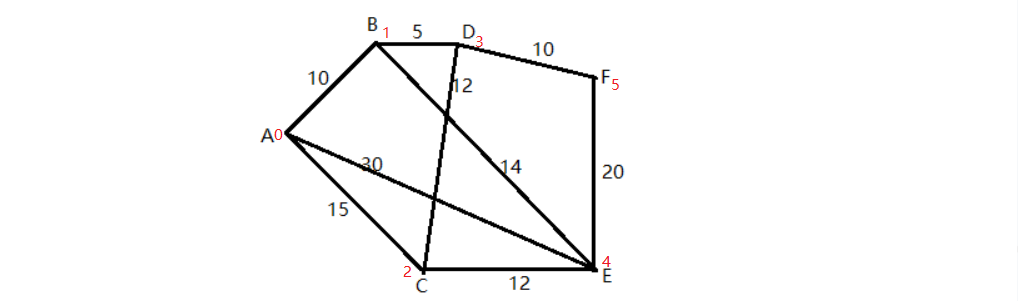
思路解析
-
算法核心1:两个矩阵
创建两个矩阵,距离D矩阵和线路P矩阵
D矩阵 [i][j]中的值代表i节点到j节点的最短距离 P矩阵 [i][j]中的值代表从i节点到j节点的最短路径中经过的第一个节点 D矩阵记录着加权图中边的权重(距离),如果两个节点没有边相连,在D矩阵中用MAX记录 P矩阵记录从i节点到j节点的最短路线中经过的第一个点。初始化D矩阵:
D 0 1 2 3 4 5 0 0 10 15 MAX 30 MAX 1 10 0 MAX 5 14 MAX 2 15 MAX 0 12 12 MAX 3 MAX 5 12 0 MAX 10 4 30 14 12 MAX 0 20 5 MAX MAX MAX 10 20 0 初始化P矩阵:
P 0 1 2 3 4 5 0 0 1 2 3 4 5 1 0 1 2 3 4 5 2 0 1 2 3 4 5 3 0 1 2 3 4 5 4 0 1 2 3 4 5 5 0 1 2 3 4 5 -
算法核心2:通过中介点缩短距离
依次令图中的节点为k节点,并使k节点作为中介节点
def create_path(n): pass def print_path(current, path, end): pass def solve_floyd(dist, start, end): """ solve_floyd方法 :param dist: 距离矩阵, 传入的矩阵记录是节点之间边的距离 :param start: 起始节点 :param end: 终止节点 :return: """ n = len(dist) path = create_path(n) # 依次设节点为中介节点 k for k in range(n): # 依次设节点为起始节点 i for i in range(n): # 依次设节点为终止节点 j for j in range(n): #判断中介节点路程长短,若更短 if dist[i][j] > dist[i][k] + dist[k][j]: # 更新D矩阵 dist[i][j] = dist[i][k] + dist[k][j] # 更新P矩阵 path[i][j] = path[i][k] # 输出最短路线 print_path(start, path, end)
代码实现
import sys
class Solution(object):
def create_path(self, n):
"""
创建P矩阵
:param n: 长度为n的二维数组
:return:
"""
path = []
for i in range(n):
row = []
for j in range(n):
row.append(j)
path.append(row)
return path
def print_path(self, current, path, end):
"""
输出
:param current: 当前节点
:param path: 当前节点路线中的下一个节点
:param end: 终点
:return:
"""
# 最短路线列表
solution = []
while current != end:
solution.append(current)
current = path[current][end]
solution.append(current)
print(solution)
def solve_floyd(self, dist, start, end):
"""
solve_floyd方法
:param dist: 距离矩阵, 传入的矩阵记录是节点之间边的距离
:param start: 起始节点
:param end: 终止节点
:return:
"""
n = len(dist)
path = self.create_path(n)
# 依次设节点为中介节点 k
for k in range(n):
# 依次设节点为起始节点 i
for i in range(n):
# 依次设节点为终止节点 j
for j in range(n):
#判断中介节点路程长短,若更短
if dist[i][j] > dist[i][k] + dist[k][j]:
# 更新D矩阵
dist[i][j] = dist[i][k] + dist[k][j]
# 更新P矩阵
path[i][j] = path[i][k]
# 输出最短路线
self.print_path(start, path, end)
max_size = sys.maxsize
D = [
[0, 10, 15, max_size, 30, max_size],
[10, 0, max_size, 5, 14, max_size],
[15, max_size, 0, 12, 12, max_size],
[max_size, 5, 12, 0, max_size, 10],
[30, 14, 12, max_size, 0, 20],
[max_size, max_size, max_size, 10, 20, 0]
]
s = Solution()
s.solve_floyd(D, 0, 5)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号