群论计数

非常简明易懂但吓人的标题。

本文非常通俗易懂，读者无需了解任何群论、置换群等等的内容。

从例题说起

给定一个 \(n\) 个点的环，有 \(m\) 种颜色给每个顶点染色，求染色方案数。旋转后相同的方案视作同一种。

Burnside 引理

枚举所有的“旋转角”\(k\)，计算 每次旋转 \(k\) 格总是相同的环 的数量，记作 \(res_k\)。取 \(res\) 的平均数即为原题所求。

这就是 Burnside 引理，证明略。

假设现在考虑旋转 \(k\) 格。对于起始顶点 \(p\)，在环上以 \(k\) 格为步长往下跳，将可以到达的点记作集合 \(S(p)=\{p+k,p+2k,\dots \pmod n\}\)，令 \(t=|S(p)|\)。无限的跳动过程经过的点的序列必然是循环的，最小循环节也就是 \(t\)。姑且把这个集合称为“轨迹”。

如何求出 \(t\) 呢？对于 \(i\in S(p)\)，由于循环的性质，就有 \(i+kt \equiv i \pmod n\)，即 \(n|kt\)。\(t\) 只需要补全 \(k\) 中缺少的 \(n\) 的因数，令 \(d=\gcd(n,k)\)，所以 \(t=n/d\)。

要想使得这个环 每次旋转 \(i\) 格总是相同，那么每个轨迹里的顶点必须染相同颜色。

Polya 定理

给定 \(i\)，怎么求 \(res_i\)？

结合例子，容易发现对于所有的 \(p\)，所构成的轨迹拼起来就能得到整个环，而且不同的轨迹之间互不相干！

有多少个互不相干的轨迹呢？很显然，所有轨迹的顶点个数是相同的，都是 \(n/t\)，即 \(d\)。联想到乘法原理，\(res_i=m^d\)。

所以答案可以表示成：

\[\frac{1}{n} \sum_{k=1}^n m^{gcd(n,k)} \]

优化

正解已经初具雏形了，但是 \(n\) 非常大，不能枚举 \(k\)。

很多数论题的精髓在于枚举什么。考虑换个角度解决问题，枚举 \(d\)。

必然有 \(d|n\)，\(d\) 的范围就确定了，而且 \(n/d\) 与 \(k/d\) 互质。欧拉函数与互质是密切相关的，\(n/d\) 是确定的，\(k\) 的取值有 \(\varphi(n/d)\) 种。因此 \(m^d\) 贡献 \(\varphi(n/d)\) 次。

综上所述，本题的最终答案就是：

\[\frac{1}{n} \sum_{d|n} m^d \varphi(\frac{n}{d}) \]

具体实现时，将 \(n\) 分解质因数，复杂度 \(O(\sqrt n)\)，在此基础上就可以快速对 \(n/d\) 分解质因数，复杂度 \(O(\log n)\)。

// Title:  Polya 定理
// Source: 模板题
// Author: Jerrywang
#include <bits/stdc++.h>
#define F first
#define S second
#define pii pair<int, int>
#define ll long long
#define rep(i, s, t) for(int i=s; i<=t; ++i)
#define debug(x) cerr<<#x<<":"<<x<<endl;
const int N=100010, mod=1e9+7;
using namespace std;

ll qp(ll x, ll y=mod-2)
{
    ll res=1;
    for(; y; y>>=1, x=x*x%mod)
        if(y&1) res=res*x%mod;
    return res;
}

int n, m;
ll phi(int x)
{
    ll res=x;
    for(int i=2; i<=x/i; i++) if(x%i==0)
    {
        res=res/i*(i-1);
        while(x%i==0) x/=i;
    }
    if(x>1) res=res/x*(x-1);
    return res;
}
ll calc(int d)
{
    return qp(m, d)*phi(n/d)%mod;
}
ll res;
void solve()
{
    scanf("%d", &n), m=n; res=0;
    for(int i=1; i<=n/i; i++) if(n%i==0)
    {
        res=(res+calc(i))%mod;
        if(i*i!=n) res=(res+calc(n/i))%mod;
    }
    res=res*qp(n)%mod;
    printf("%lld\n", res);
}

int main()
{
    #ifdef Jerrywang
    freopen("E:/OI/in.txt", "r", stdin);
    #endif
    int T; scanf("%d", &T);
    while(T--) solve();
    
    return 0;
}

继续思考：翻转同构？

沿着上面的思路继续思考。刚才枚举旋转角，现在枚举对称轴，共有 \(n\) 条，依次考虑。

如果 \(n\) 是奇数，对称轴由一个顶点穿向对面的边，如下图：

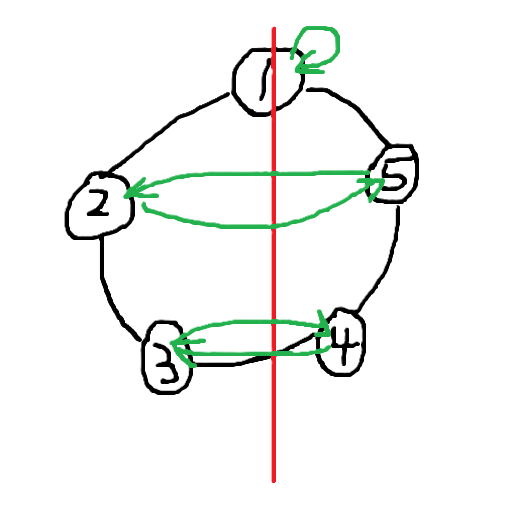
绿箭头表示在对称条件下的轨迹，轨迹仍然需要满足：拼起来就能得到整个环，而且不同的轨迹之间互不相干！

最终答案是：

\[\frac{1}{2n} (\sum_{k=1}^n m^{gcd(n,k)}+nm^{\frac{n+1}{2}}) \]

如果 \(n\) 是偶数，\(n/2\) 条对称轴由一个顶点穿向对面的一个顶点，如下图：

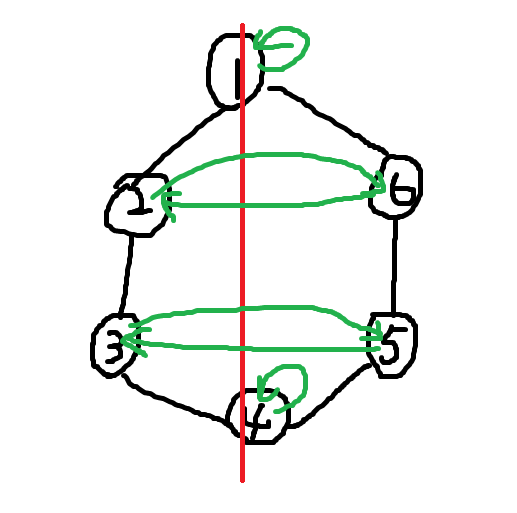
\(n/2\) 条对称轴还可以由一条边穿向对面的一条边，如下图：

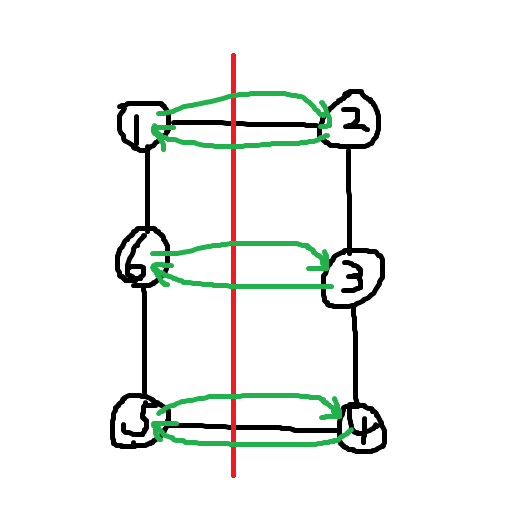
最终答案是：

\[\frac{1}{2n} (\sum_{k=1}^n m^{gcd(n,k)}+\frac{n}{2} m^{\frac{n}{2}+1}+\frac{n}{2} m^{\frac{n}{2}}) \]

本题数据范围极小，不必优化即可通过。

// Title:  Let it Bead
// Source: POJ2409
// Author: Jerrywang
#include <cstdio>
#define F first
#define S second
#define pii pair<int, int>
#define ll long long
#define rep(i, s, t) for(int i=s; i<=t; ++i)
#define debug(x) cerr<<#x<<":"<<x<<endl;
const int N=100010;
using namespace std;

int m, n;
ll qp(ll x, ll y)
{
    ll s=1;
    for(; y; y>>=1, x=x*x)
        if(y&1) s=s*x;
    return s;
}
int gcd(int a, int b)
{
    return b?gcd(b, a%b):a;
}
void solve()
{
    ll res=0;
    rep(k, 1, n) res+=qp(m, gcd(n, k));
    if(n&1) res+=n*qp(m, (n+1)/2);
    else res+=n/2*qp(m, n/2+1)+n/2*qp(m, n/2);
    printf("%lld\n", res/2/n);
}

int main()
{
    #ifdef Jerrywang
    freopen("E:/OI/in.txt", "r", stdin);
    #endif
    while(scanf("%d%d", &m, &n), m+n) solve();
    
    return 0;
}