【树】力扣99：恢复二叉搜索树

给你二叉搜索树的根节点 root ，该树中 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树。

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？

示例1：

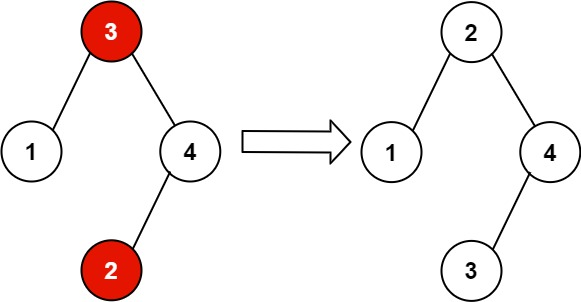
输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

示例2：

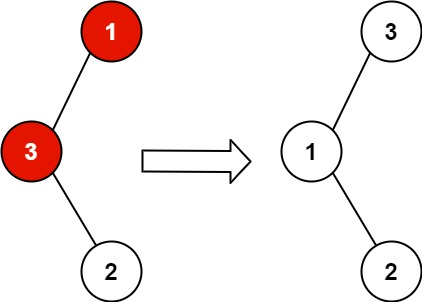
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

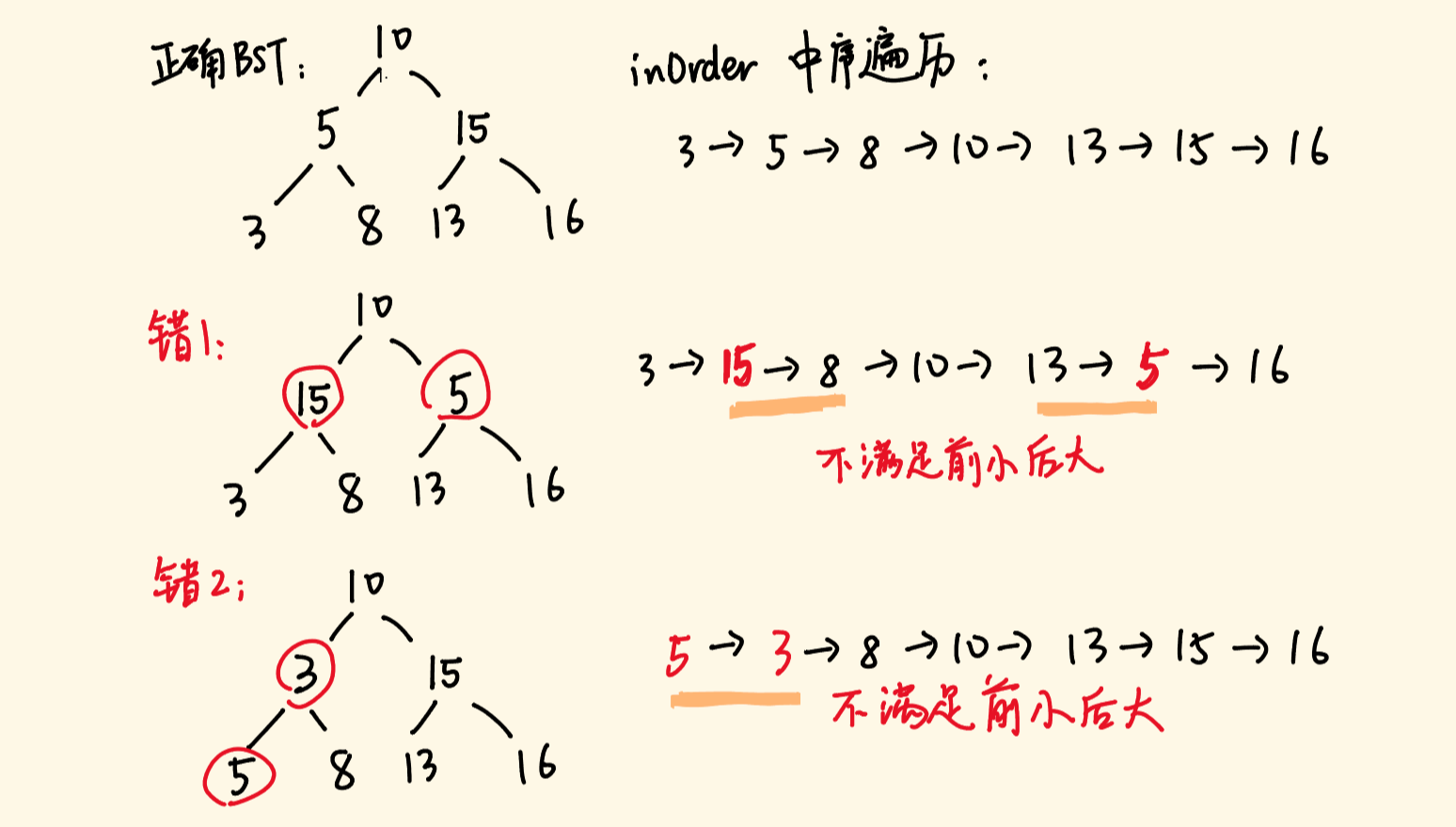
二叉搜索树中序遍历数组的值是递增有序的。如果错误地交换了两个结点，等于在这个数组中交换了两个值，破坏了递增性。

有一个技巧:

• 如果遍历整个序列过程中只出现一对不满足查找树的，交换这一对元素即可

• 如果出现两对不满足的，需要交换第一对的第一个元素与第二对的第二个元素

中序遍历可以用递归，也可以用迭代。

方法一

遍历过程中，将结点值推入一个列表 inorder，再遍历列表找出错误对。

此处用递归实现中序遍历。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def recoverTree(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        if not root:
            return None
        # 中序遍历
        inorder = []
        def dfs(node):
            if not node:
                return
            dfs(node.left)
            inorder.append(node)
            dfs(node.right)
        dfs(root)
        # 找错误对
        firstNode, secondNode = None, None # 交换了的两个结点
        pre = inorder[0]
        for i in range(1, len(inorder)):
            # 第一次出现不正常的情况，pre 就是第一个不正常的结点，赋给 firstNode，而 pre 后一个结点赋给 secondNode，这样的话，如果第二组错误结点没出现，就说明交换的结点是相邻结点，出现了则只调整secondNode
            if pre.val > inorder[i].val:
                secondNode = inorder[i]
                if not firstNode: # 调整 firstNode 的情况只在第一次出现的情况，此时为空值
                    firstNode = pre
            pre = inorder[i]
        # 此时遍历结束，确定了待交换的两个错误点
        # 如果两个变量不为空值，说明存在错误结点，则交换结点值
        if firstNode and secondNode:
            firstNode.val, secondNode.val = secondNode.val, firstNode.val

时间复杂度：O(N)，其中 N 为二叉搜索树的结点数。中序遍历需要 O(N) 的时间，判断两个交换结点在最好的情况下是 O(1)，在最坏的情况下是 O(N)，因此总时间复杂度为 O(N)。

空间复杂度：O(N)。需要用 inorder 数组存储树的中序遍历列表。

方法一的改进

新建数组没有必要。

实际上，只需要关心中序遍历的值序列中每个相邻的位置的大小关系是否满足条件，且错误交换后最多两个位置不满足条件，因此在中序遍历的过程只需要比较前后访问的结点值，则增加一个辅助的 cur 指针，pre 保存上一个访问的结点，当前访问的是 cur 结点。

每访问一个结点，如果 pre.val > cur.val，就找到了一对“错误对”。如果不满足说明找到了一个交换的结点，且最多在找到两次以后就可以终止遍历。

遍历结束，就确定了待交换的两个错误点，进行交换。

此处用迭代实现中序遍历。

class Solution:
    def recoverTree(self, root: Optional[TreeNode]) -> None:
        if not root:
            return None

        x, y = None, None
        pre = TreeNode(float("-inf"))
        # 中序遍历
        stack = []
        cur = root
        while cur or stack:
            while cur:
                stack.append(cur)
                cur = cur.left
            cur = stack.pop()
            # 边遍历边找
            if pre.val > cur.val and not x: # 第一组已确定，记录第一个点
                x = pre
            if pre.val > cur.val and x: # 第一组，如果有第二组就继续更新 y
                y = cur
            pre= cur
            # 判断完了再继续循环
            cur = cur.right
        x.val, y.val = y.val, x.val

时间复杂度：最坏情况下（即待交换结点为二叉搜索树最右侧的叶子节点）需要遍历整棵树，时间复杂度为 O(N)，其中 N 为二叉搜索树的节点个数。

空间复杂度：O(H)，其中 H 为二叉搜索树的高度。中序遍历的时候栈的深度取决于二叉搜索树的高度。

可以看出，无论是用递归的方式遍历，还是用手动模拟栈的方式遍历，都没有达到真正的常数空间。因此需要用到更高级的方法进行中序遍历。

Morris 中序遍历（满足常数空间）

假设当前遍历到的结点为 cur，Morris 遍历算法的步骤如下：

• 如果 cur 无左孩子，则访问 cur 的右孩子，即 cur = cur.right

• 如果 cur 有左孩子，则找到 cur 左子树上最右的结点（即左子树中序遍历的最后一个结点，也就是 cur 在中序遍历中的前驱结点 predecessor），记为 pred。根据 pred 的右孩子是否为空，进行如下操作：

  • 如果 pred 的右孩子为空，则将其右孩子指向 cur，然后访问 cur 的左孩子，即 cur = cur.left。
  • 如果 pred 的右孩子不为空，则此时其右孩子指向 cur，说明已经遍历完 cur 的左子树。将 pred 的右孩子置空，然后访问 cur 的右孩子，即 cur = cur.right

• 重复上述操作，直至访问完这整棵树

其实整个过程只多做一步：将当前结点左子树中最右边的结点指向它，这样在左子树遍历完成后通过这个指向走回了 cur，且能再通过这个知道已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

注意：破坏的现场一定要还原回来，不可以在找到第二组错误对时直接break出循环

class Solution(object):
    def recoverTree(self, root):
        x, y = None, None # 初始化储存两个错误结点的变量
        pred, tmp = None, None # pred 记录中序遍历当前结点 root 的前驱，tmp 是完成 Morris 连接的寻找前驱的指针（也可以再用一个变量 cur 维护当前结点，看起来更直观）
        while root: # 当前结点为空时说明所有结点遍历结束
            if root.left: # 当左子树不为空，访问当前结点 root 的最近左结点，去找这个子树的最右结点
                tmp = root.left
                while tmp.right and tmp.right != root: # 找没遍历过的左子树的最右结点
                    tmp = tmp.right
                if tmp.right is None: # 到达了左子树的最右结点，就断开当前结点 root 的前驱连接，将 root 连到这个最右结点上
                    tmp.right = root
                    root = root.left
                else:
                    if pred and pred.val > root.val:
                        y = root
                        if not x:
                            x = pred
                    pred = root # 更新前驱,为下一个结点做准备
                    tmp.right = None # 还原
                    root = root.right # 访问 root 的右子树
            else: # 左子树为空
                if pred and pred.val > root.val:
                    y = root
                    if not x:
                        x = pred
                pred = root
                root = root.right
        if x and y:
            x.val, y.val = y.val, x.val

时间复杂度：O(N)，其中 N 为二叉搜索树的高度。Morris 遍历中每个结点会被访问两次，因此总时间复杂度为 O(2N) = O(N)。

空间复杂度：O(1)。