【树】力扣543：二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

注意：两结点之间的路径长度是以它们之间边的数目表示。

示例：

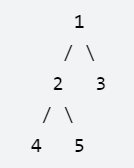
输入：
输出：3
它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]

一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）就是求路径经过节点数的最大值减一，等效于 该路径的根结点的左右子树最大高度之和。

因此这道题也是 力扣104. 二叉树的最大深度 的变形。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        self.maxd = 0
        depth(root) # 从树的根节点开始递归函数depth
        return self.maxd

    # 求出以各结点为根结点的树的最大深度
        def depth(node):
            if not node:
                return 0
            left, right = depth(node.left), depth(node.right) # 左右子树的最大深度
            self.maxd = max(left + right, self.maxd) # 每个结点都要去判断该结点的左子树 + 右子树的深度（即当前直径）是否大于self.maxd，更新最大值
            return 1 + max(left, right)

全局变量不加self.的下场：

时间复杂度：O(N)，其中 N 为二叉树的节点数，即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。

空间复杂度：O(Height)，其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，而递归的深度显然为二叉树的高度，并且每次递归调用的函数里又只用了常数个变量，所以所需空间复杂度为 O(Height) 。