[LeetCode] 849. Maximize Distance to Closest Person_Medium tag: BFS, array

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized. 

Return that maximum distance to the closest person.

 

Example 1:

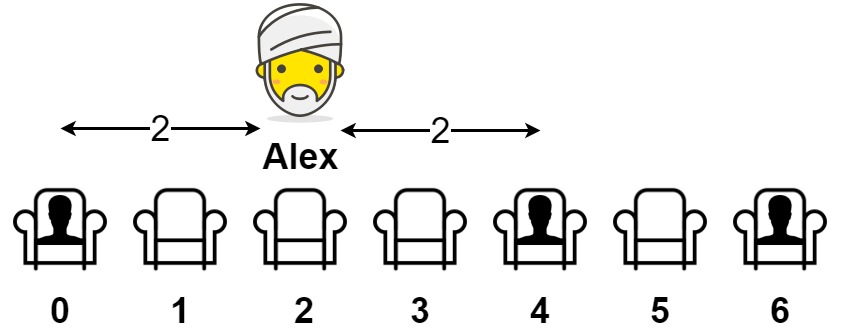
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

Input: seats = [1,0,0,0]
Output: 3
Explanation: 
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3:

Input: seats = [0,1]
Output: 1

 

Constraints:

• 2 <= seats.length <= 2 * 104
• seats[i] is 0 or 1.
• At least one seat is empty.
• At least one seat is occupied.

 

Ideas:

1. T: O(n)       S: O(n)

直接用BFS，跟[LeetCode] 286. Walls and Gates_Medium tag: BFS 题目类似，只是2D array 变成了1D array

Code:

class Solution:
    def maxDistToClosest(self, seats: List[int]) -> int:
        queue, visited, ans, n = collections.deque([]), set(), 0, len(seats)
        for index, seat in enumerate(seats):
            if seat:
                queue.append((index, 0))
                visited.add(index)
        while queue:
            seat, dis = queue.popleft()
            ans = max(ans, dis)
            for dif in [1, -1]:
                new_seat = seat + dif
                if 0 <= new_seat < n and new_seat not in visited:
                    visited.add(new_seat)
                    queue.append((new_seat, dis + 1))
        return ans

 

 

2. T: O(n)     S: O(1)

直接找为0 的group的每个group的个数，然后用ans = max(ans, (count + 1)//2); 如果是开头start == 0或者结尾 i == n则是k，注意这个edge case.

Code:

class Solution:
    def maxDistToClosest(self, seats: List[int]) -> int:
        ans, i, count, n = 0, 0, 0, len(seats)
        while i < n:
            if seats[i] == 0:
                count = 0
                start = i
                while i < n and seats[i] == 0:
                    i += 1
                    count += 1
                candidate = count if start == 0 or i == n else (count + 1)//2
                ans = max(ans, candidate)
            else:
                i += 1
        return ans