两角和差公式的证明

经典法

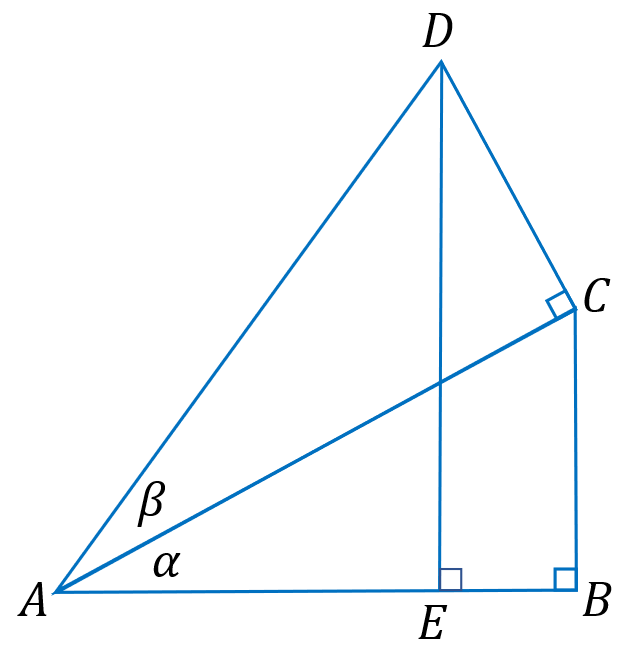
上图可知：sinα＝CB/AC，sinβ＝DC/AD； cosα＝AB/AC，cosβ＝AC/AD；sin(α＋β)＝DE/AD；
因 CB＝AC·sinα 且 AC=AD·cosβ 则 CB＝AD·cosβ·sinα （1）
做辅助线得到下图

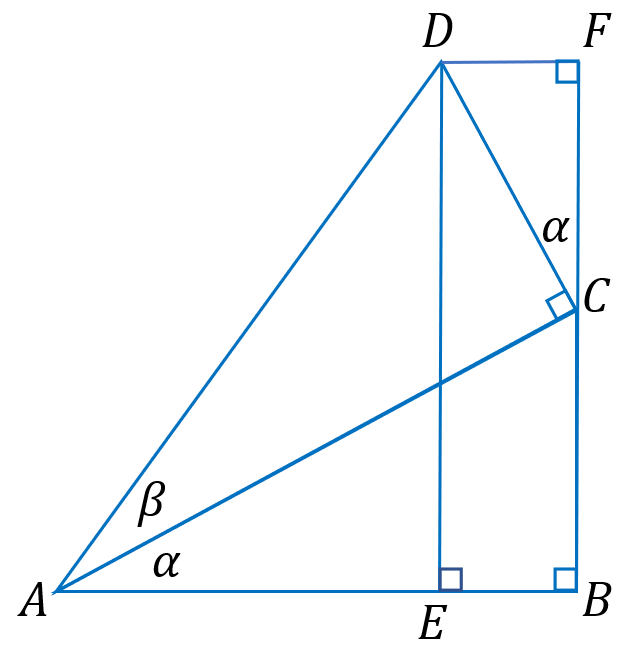
由上图可知：cosα＝CF/CD 且 CD＝AD·sinβ 则 CF＝AD·sinβcosα （2）
由（1)和（2）知：CF＋CB＝AD·sinβcosα+AD·cosβ·sinα=AD·(sinβcosα+cosβ·sinα） （3）
由上图还可知：DE=AD·sin(α+β) （4）
由上图还可知：CF＋CB＝FB 且FB=DE 则 CF+CB=DE （5）
由（3）（4）（5）式 可推到出 AD·(sinβcosα+cosβ·sinα）=AD·sin(α+β)
即可正得 sin(α+β) =sinβcosα+cosβ·sinα

面积法

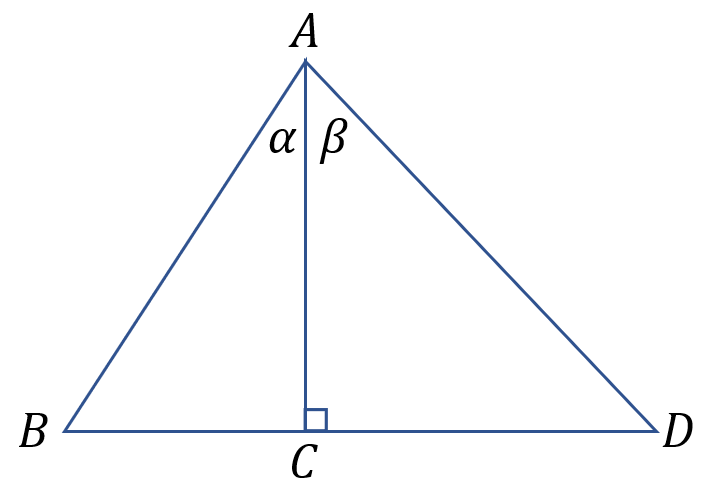
从上图可以得到：\(sinα＝BC/AB，sinβ＝DC/AC； cosα＝AC/AB，cosβ＝AC/AD\)。
推出：\(BC＝AB·sinα，CD＝AC·sinβ，AC＝AB·cosα＝AD·cosβ\)。
左边三角形 \(S_{△ABC}＝\frac{1}{2}·BC·AC＝(AB·sinα)·(AD·cosβ)=\frac{1}{2}AB·AD·sinαcosβ\) (1)
右边三角形 \(S_{△ACD}＝\frac{1}{2}·CD·AC＝(AD·sinβ)·(AB·cosα)=\frac{1}{2}AB·AD·cosαsinβ\) (2)
根据 \(S=\frac{1}{2}abSinC\) 公式（已知任意两边长度a,b，及两边夹角C)
则整个三角形的面积 \(S_{△ABD}＝\frac{1}{2}·AB·AD·sin(α＋β)\)；（3）
因为 \(S_{△ABC}+S_{△ACD}=S_{△ABD}\) .并将（1）（2）（3）带入可得到如下等式
\(\qquad \quad\frac{1}{2}AB·AD·sinαcosβ+\frac{1}{2}AB·AD·cosαsinβ=\frac{1}{2}·AB·AD·sin(α＋β)\)
\(\qquad \quad\frac{1}{2}AB·AD·(sinαcosβ+cosαsinβ)=\frac{1}{2}·AB·AD·sin(α＋β)\)
化简整理得：\(sin(α＋β)＝sinαcosβ＋cosαsinβ\)

距离公式+全等三角形

此方法人教版2000年10月第2版高中数学第一册（下）的证明方法

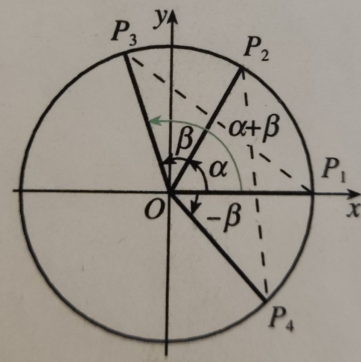
由图知P1、P2、P3、P4的坐标分别是
P1(1,0)
P2(cosα,sina)
P3(cos(α+β),sin(α+β))
P4(cons(-β),sin(-β))
根据平面两点\(P_1(x_1,y_1),P_2(y_1,y_2)\)间距离公式\(P_1P_2=\sqrt{(x_2-x_1)^2-(y_2-y_1)^2}\)
\(P_1P_3=[cos(α+β)-1]^2+[sin(α+β)-0]^2=cos^2(α+β)-2cos(α+β)+1+sin^2(α+β)=2-2cos(α+β)\)
\(P_2P_4=[cos(-β)-cosα]^2+[sin(-β)-sinα]^2=cos^2β-2cos(-β)cosα+cos^2α+sin^2(β)-2sin(-β)sinα+sin^2α=2-2(cosαcosβ-sinαsinβ)\)
因\(△P_2OP_4 \cong △P_1OP_3\) 则\(P_1P_3=P_2P_4\)
即\(2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)\)
整理得\(cos(α+β)=cosαcosβ-sinαsinβ\)

向量法

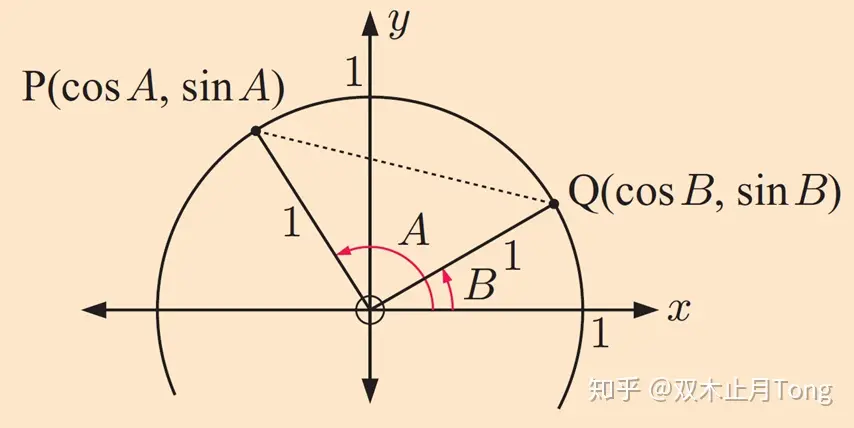在单位圆上取两个角 $\angle A,\angle B $，其终边与单位圆的交点分别是P与Q，其坐标分别为$\mathrm{P}(\cos A, \sin A) ， \mathrm{Q} (\cos B, \sin B) $

\(\overrightarrow{O Q} \cdot \overrightarrow{O P}=|\overrightarrow{O Q}| \cdot|\overrightarrow{O P}| \cos (A-B)=\cos A \cos B+\sin A \sin B\)
而 \(|\overrightarrow{O Q}| =|\overrightarrow{O P}|=1\) ，所以
$\boxed{\cos (A-B)=\cos A \cos B+\sin A \sin B} $。

欧拉公式法

参考链接
三角函数的任督二脉：和角公式的多种证明方法
如何记住所有的三角函数公式？