洛谷 - P2532 [AHOI2012] 树屋阶梯 -- AcWing - 1317. 树屋阶梯

洛谷 - 题目链接

AcWing - 题目链接

考察知识点

• 数学 - 高精度
• 数学 - 组合数学 - 卡特兰数

思路分析

当 \(N=0\) 时，不放置钢材是一种方案，答案为1。

当 \(N=1\) 时，存在1种放置方案：

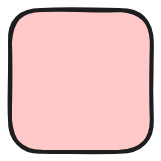
当 \(N=2\) 时，存在2种放置方案：

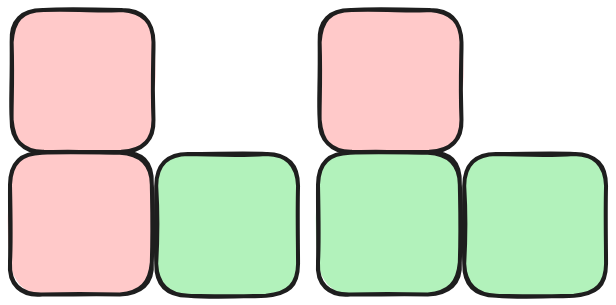
当 \(N=3\) 时，存在5种放置方案：

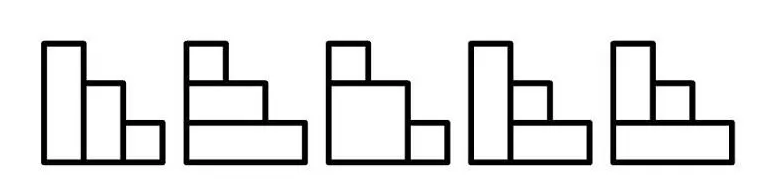
当 \(N=4\) 时，存在14种放置方案：

于是我们神奇地发现，当 \(N=i\) 时，答案就是 \(C_i\)（卡特兰数列的第 \(i\) 项）。

但这种方法过于玄学，所以我们严谨地证明一下：

假设 \(N=4\)，记 \(N=i\) 时的答案为 \(f_i\)。

给出一张未进行钢材分配的树屋阶梯的示意图。

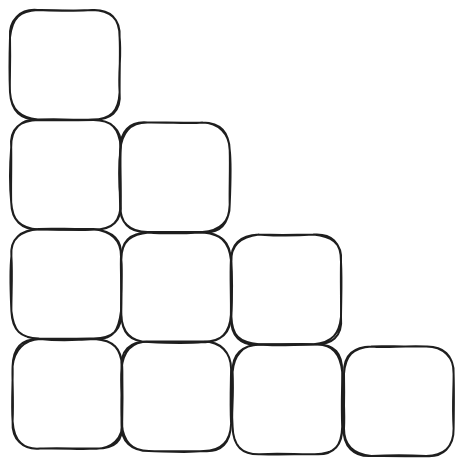
由于钢材是矩形的且仅有 \(N\) 块，而每行阶梯的右侧拐角也有 \(N\) 个，所以每个矩形必定覆盖且仅覆盖一个角落。

设左下角点为O点，枚举每个覆盖O点且覆盖一个角落的矩形，有以下4种情况：

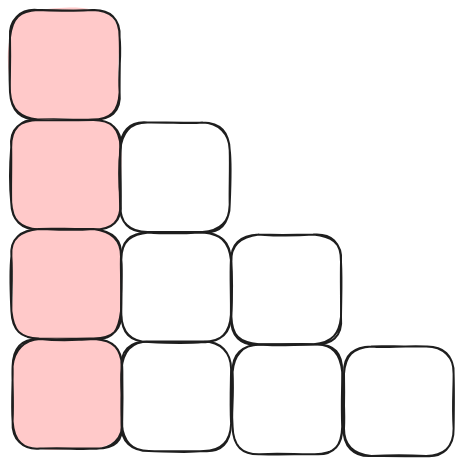
矩形上面方案数为 \(f_0\)，矩形右面方案数为 \(f_3\)，由乘法原理可得，这种情况下方案总数为 \(f_0 \times f_3\)。

同理可得：

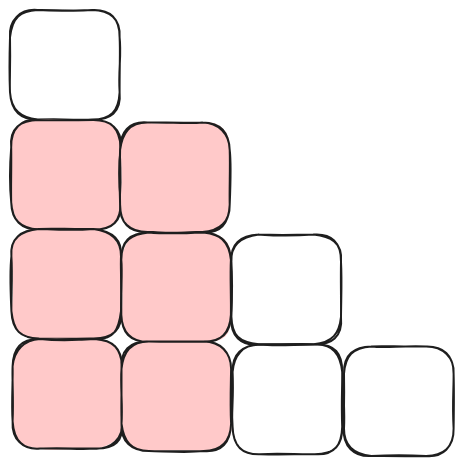
这种情况下，矩形上面方案数为 \(f_1\)，矩形右面方案数为 \(f_2\)，由乘法原理可得，这种情况下方案总数为 \(f_1 \times f_2\)。

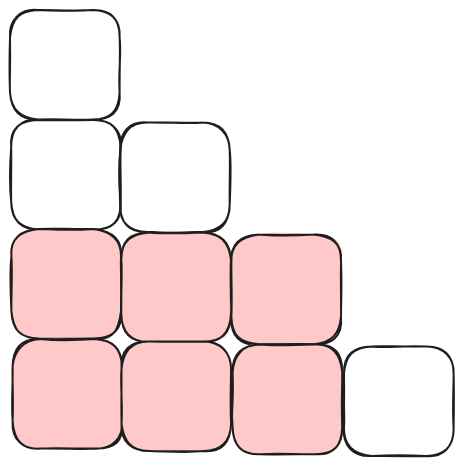
这种情况下，矩形上面方案数为 \(f_2\)，矩形右面方案数为 \(f_1\)，由乘法原理可得，这种情况下方案总数为 \(f_2 \times f_1\)。

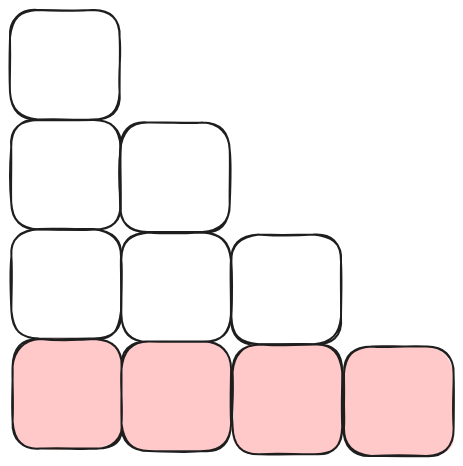
这种情况下，矩形上面方案数为 \(f_3\)，矩形右面方案数为 \(f_0\)，由乘法原理可得，这种情况下方案总数为 \(f_3 \times f_0\)。

由上述4种情况结合加法原理可得，\(f_4=f_0 \times f_3+f_1 \times f_2+f_2 \times f_1+f_3 \times f_0\)。

更一般地，\(f_n=\begin{cases} 1(n=0)\\ \begin{aligned} \sum_{i=0}^{n-1} f_i \times f_{n-1-i} \end{aligned},(n \ge 0)\end{cases}\)。

这就是卡特兰数递推公式。

那为什么这就是卡特兰数递推公式呢？

回忆卡特兰数列的经典应用——n 个元素的出栈序列：

问题：n 个元素（如 1,2,3,...,n）依次入栈，求不同的出栈序列总数。

证明：

1. 假设第一个出栈的元素是第 k 个入栈的元素（k 从 1 到 n）：

• 第 \(k\) 个元素出栈前，必须先将前 \(k-1\) 个元素入栈并全部出栈（否则第 \(k\) 个元素无法先出栈），这部分的出栈序列数为 \(C_{k-1}\)（对应 \(k-1\) 个元素的出栈问题）。
• 第 k 个元素出栈后，剩下的 \(n-k\) 个元素（第 \(k+1\) 到第 \(n\) 个）需要入栈并出栈，这部分的出栈序列数为 \(C_{n-k}\)（对应 \(n-k\) 个元素的出栈问题）。

2. 总序列数 = 所有可能 “第一个出栈元素” 对应的 “前 k-1 个序列数 \(\times\) 后 n-k 个序列数” 之和，即： \(C_n=\begin{aligned} \sum_{k=1}^n C_{k-1} \times C_{n-k} \end{aligned}\)。

3. 令 \(i=k-1\)（则 \(k\) 从 1 到 n 对应 i 从 0 到 n-1），代入后公式变为： \(C_n=\begin{aligned} \sum_{i=0}^{n-1} C_i \times C_{n-1-i} \end{aligned}\)。

而 n 个元素的出栈序列数，正是卡特兰数 \(C_n\) 的另一个经典定义——这证明了该求和公式与卡特兰数的等价性。

因此，当 \(N=n\) 时，答案即为 \(C_i\)。

在这个题里，我们可以用卡特兰数计算公式来求 \(C_n\)：\(C_n=\frac{(2 \times n)!}{n! \times (n+1)!}\)，化简可得 \(C_n=\frac{\begin{aligned} \prod_{i=n+2}^{2 \times n} i \end{aligned}}{n!}\)。

注意：本题 \(1 \leq N \leq 500\)，要用高精度。

时间复杂度

\(O(n \times log_{10} C_{n})\)（\(C_{n}\) 表示卡特兰数列的第 \(n\) 项）

C++代码

// Problem: P2532 [AHOI2012] 树屋阶梯
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2532
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Problem: 树屋阶梯
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/description/1319/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

int n;  // 阶梯的高度，即需要构建n阶阶梯

// 高精度乘法函数：将大整数A（逆序存储，低位在前）与整数b相乘
// 参数：A为被乘数（逆序vector），b为乘数（整数）
// 返回值：乘积结果（逆序vector）
vector<int> mul(vector<int> &A, int b) {
    vector<int> C;  // 存储乘法结果的容器（逆序）
    int t = 0;      // 用于存储进位值，初始为0
    
    // 遍历A的每一位，或当存在进位时继续计算
    for (int i = 0; i < A.size() || t; i++) {
        // 若当前位在A的范围内，将A[i]与b的乘积累加到进位t中
        if (i < A.size()) t += A[i] * b;
        // 将t的个位作为结果的当前位（逆序存储）
        C.push_back(t % 10);
        // 更新进位t为t的十位及以上部分
        t /= 10;
    }
    
    // 去除结果末尾的无效0（仅当长度大于1时，避免单个0被误删）
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C;  // 返回乘法结果
}

// 高精度除法函数：将大整数A（逆序存储，低位在前）除以整数b
// 参数：A为被除数（逆序vector），b为除数（整数）
// 返回值：商（逆序vector），余数通过局部变量r处理（本题无需返回）
vector<int> div(vector<int> A, int b) {
    vector<int> C;  // 存储商的容器（先正序后逆序）
    int r = 0;      // 存储余数，初始为0
    
    // 从A的最高位（vector末尾，因A是逆序存储）开始计算
    for (int i = A.size() - 1; i >= 0; i--) {
        // 余数乘以10加上当前位数字，形成新的被除数
        r = r * 10 + A[i];
        // 计算当前位的商并存入C（此时C为正序存储）
        C.push_back(r / b);
        // 更新余数为新被除数除以b的余数
        r %= b;
    }
    
    // 将商从正序转为逆序（与乘法结果格式保持一致）
    reverse(C.begin(), C.end());
    
    // 去除结果末尾的无效0（仅当长度大于1时）
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C;  // 返回除法结果
}

int main() {
    scanf("%d", &n);  // 读取阶梯高度n
    
    vector<int> ans;  // 存储最终结果的高精度容器（逆序）
    ans.push_back(1); // 初始化结果为1（乘法的起始值）
    
    // 计算卡特兰数的分子部分：(n+2) × (n+3) × ... × (2n)
    // 卡特兰数公式：C(n) = (2n)! / [ (n+1)! × n! ]
    // 此处分子等价于 (2n)! / (n+1)! 
    for (int i = n + 2; i <= 2 * n; i++) {
        ans = mul(ans, i);  // 累乘计算分子
    }
    
    // 计算卡特兰数的分母部分：除以n!（1×2×...×n）
    // 完成公式中的除以n!操作，得到最终卡特兰数
    for (int i = 1; i <= n; i++) {
        ans = div(ans, i);  // 累除计算分母
    }
    
    // 输出结果：从最高位（vector末尾）到最低位（vector开头）依次打印
    for (int i = ans.size() - 1; i >= 0; i--) {
        printf("%d", ans[i]);
    }
    puts("");  // 输出换行符，确保格式正确
    
    return 0;
}