实验3

实验任务1

task1.c

点击查看代码

#include <stdio.h>
char score_to_grade(int score);
int main() {
	int score;
	char grade;
	while (scanf("%d", &score) != EOF) {
		grade = score_to_grade(score);
		printf("分数: %d, 等级: %c\n\n", score, grade);
	}
	return 0;
}
char score_to_grade(int score) {
	char ans;
	switch (score / 10) {
	case 10:
	case 9: ans = 'A'; break;
	case 8: ans = 'B'; break;
	case 7: ans = 'C'; break;
	case 6: ans = 'D'; break;
	default:ans = 'E';
	}
	return ans;
}

问题一：这个函数可以将分数转化为等第；形参为整形；返回值为字符型。

问题二：如果改为问题中的形式，代码将会输出包括该分数对应等第及以下所有等第。

实验任务2

task2.c

点击查看代码

#include <stdio.h>
int sum_digits(int n);
int main() {
	int n;
	int ans;
	while (printf("Enter n: "), scanf("%d", &n) != EOF) {
		ans = sum_digits(n); 
		printf("n = %d, ans = %d\n\n", n, ans);
	}
	return 0;
}
int sum_digits(int n) {
	int ans = 0;
	while (n != 0) {
		ans += n % 10;
		n /= 10;
	}
	return ans;
}

问题1：该函数是用于求输入的数的各个数位上数之和。

问题2：将函数改为题目中那样同样可以实现原函数相同的功能；原函数是使用迭代的思想，分别将各数位上的数求出来并加到sum上；而改后的函数则是使用递归的思想，将没求出来的式子暂时保留，直到到达函数的出口时，再不断向前求出函数的值。

实验任务3

task3.c

点击查看代码

int power(int x, int n);   
int main() {
    int x, n;
    int ans;
    while(printf("Enter x and n: "), scanf("%d%d", &x, &n) != EOF) {
        ans = power(x, n);  
        printf("n = %d, ans = %d\n\n", n, ans);
    }
    
    return 0;
}
#include <stdio.h>
int power(int x, int n) {
    int t;
    if(n == 0)
        return 1;
    else if(n % 2)
        return x * power(x, n-1);
    else {
        t = power(x, n/2);
        return t*t;
    }
}

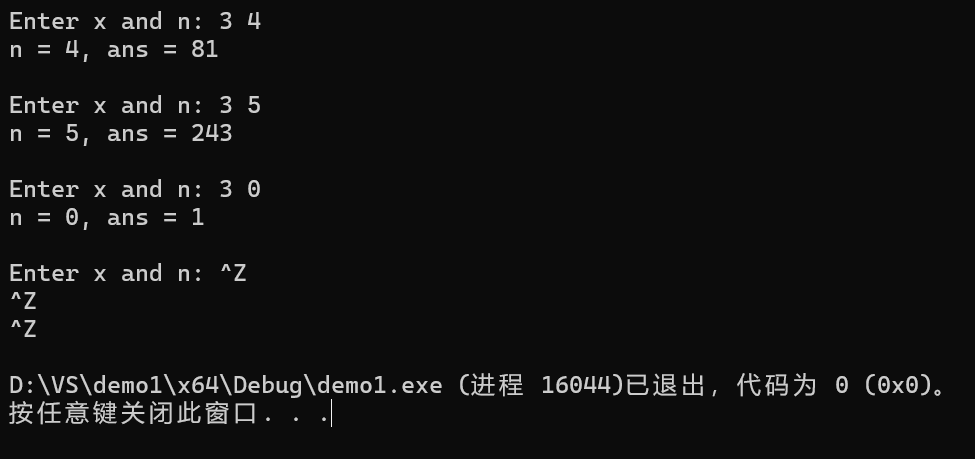
问题1：该函数用于求x的n次方。

问题2：是递归函数，公式为：
x^n = x* x^(n-1) ;
x^n = [ x^(n/2) ] ^2 , (n为偶数) ;
x^0 = 1 。

实验任务4

task4.c

点击查看代码

#include<stdio.h>
int is_prime(int);
int main()
{
	int sum = 0;
	for (int i = 1; i < 98; i++)
	{
		if (is_prime(i) && is_prime(i + 2))
		{
			printf("%d %d\n", i, i + 2);
			sum++;
		}
	}
	printf("100以内的孪生素数有 %d 个。", sum);
	return 0;
}
int is_prime(x)
{
	if (x == 1)
		return 0;
	for (int i = 2; i <=x/2; i++)
	{
		if (x % i == 0)
		{
			return 0;
		}
	}
	return 1;
}

实验任务5

task5_1.c

迭代算法

点击查看代码

#include <stdio.h>
int func(int n, int m);
int main() {
	int n, m;
	int ans;
	while (scanf_s("%d%d", &n, &m) != EOF) 
	{
		ans = func(n, m); 
		printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
	}
	return 0;
}
int func(n, m)
{
	if (m > n)
		return 0;
	int result = 1;
	for (int i = 0; i <= m - 1; i++)
		result *= (n - i);
	for (int i = 1; i <= m; i++)
		result /= i;
	return result;
}

task5_2.c

递归算法

点击查看代码

#include <stdio.h>
int func(int n, int m);
int main() {
	int n, m;
	int ans;
	while (scanf_s("%d%d", &n, &m) != EOF)
	{
		ans = func(n, m);
		printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
	}
	return 0;
}
int func(n, m)
{
	if (m > n)
		return 0;
	if (m == 0 || m == n)
		return 1;
	return func(n - 1, m) + func(n - 1, m - 1);
}

实验任务6

点击查看代码

#include <stdio.h>
int gcd(int, int, int);
int main()
{
	int a, b, c;
	int ans;
	while (scanf("%d%d%d", &a, &b, &c) != EOF)
	{
		ans = gcd(a, b, c);
		printf("最大公约数: %d\n\n", ans);
	}
	return 0;
}
int gcd(a, b, c)
{
	int r, s;
	do
	{
		r = a % b;
		a = b;
		b = r;
	} while (r!=0);
	do
	{
		s = a % c;
		a = c;
		c = s;
	} while (s!=0);
	return a;
}

实验任务7

task7.c

点击查看代码

#include <stdio.h>
#include <stdlib.h>
void print_charman(int);
int main() {
	int n;
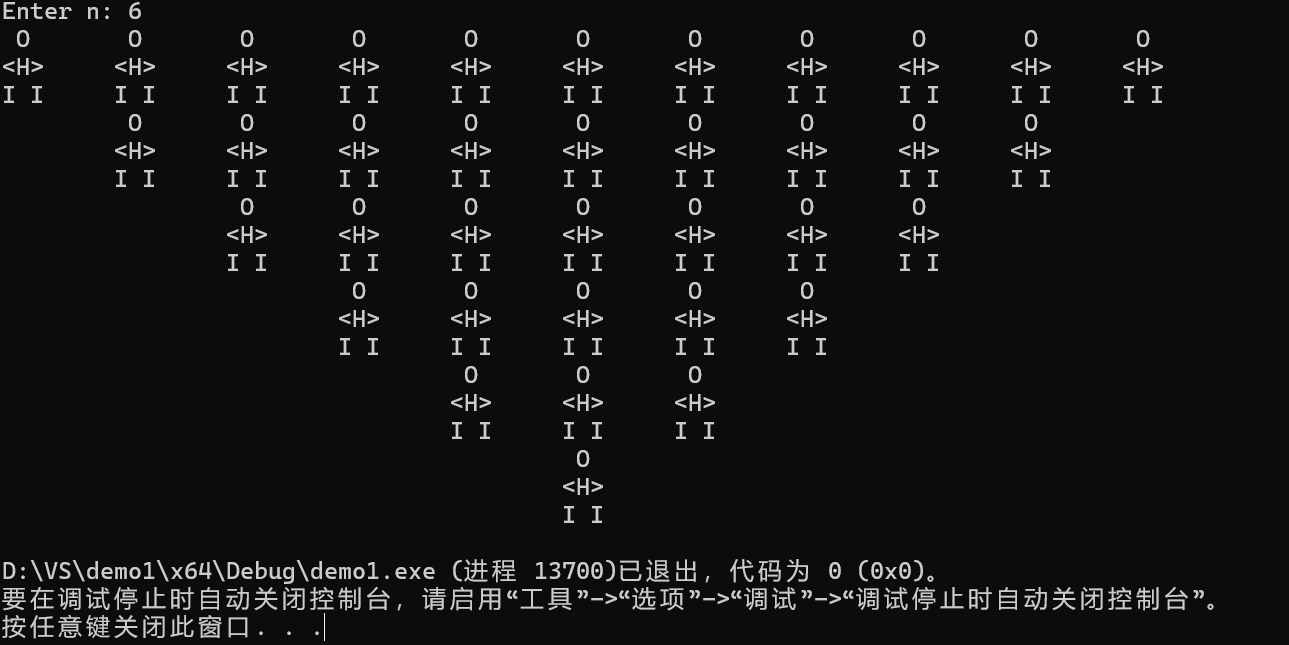
	printf("Enter n: ");
	scanf("%d", &n);
	print_charman(n);

	return 0;
}
void print_charman(int n)
{
	int row=2*n-1, line=1;
	for (; line <= n; row=row-2, line++)
	{
		for (int i1 = 1; i1 < line; i1++)
		{
			printf("\t");
		}
		for (int i1 = 0; i1 < row; i1++)
		{
			printf(" O \t");
		}
		printf("\n");
		for (int i1 = 1; i1 < line; i1++)
		{
			printf("\t");
		}
		for (int i1 = 0; i1 < row; i1++)
		{
			printf("<H>\t");
		}
		printf("\n");
		for (int i1 = 1; i1 < line; i1++)
		{
			printf("\t");
		}
		for (int i1 = 0; i1 < row; i1++)
		{
			printf("I I\t");
		}
		printf("\n");
	}
}