AI4Weather（一）

Mamba: Linear-Time Sequence Modeling with Selective State Spaces

Transformer在长序列处理中存在计算效率瓶颈，而线形注意力、门控卷积、循环模型以及SSM等多种亚二次时间复杂度的架构由于无法执行基于内容的推理，表现始终逊于Transformer。

以下内容参考https://blog.csdn.net/v_JULY_v/article/details/134923301。

State Space Models(SSM)

SSM

SSM一般用连续时间来表示\(\begin{cases}h'(t)=Ah(t)+Bx(t) \\ y(t)=Ch(t)\color{gray}{+Dx(t)}\end{cases}\)，其中\(x(t),y(t)\)分别代表输入和输出，\(h(t)\)为隐状态，\(A,B,C\)为可学习的参数。

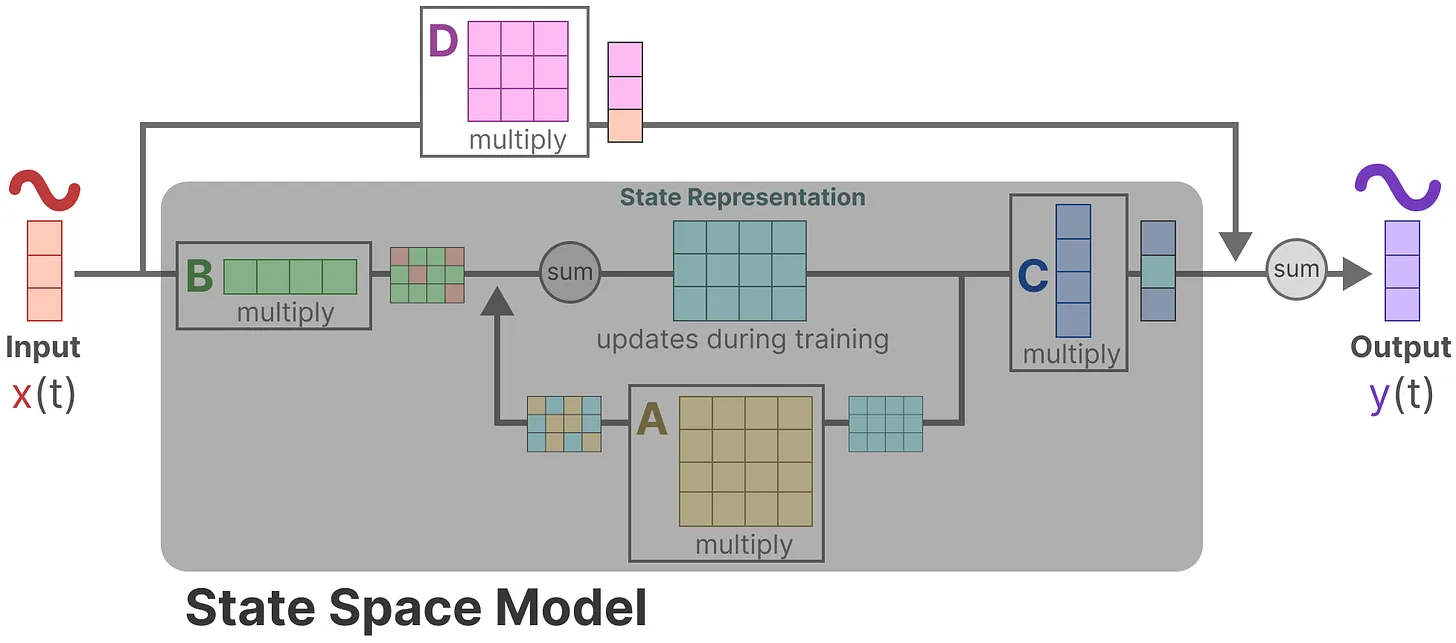
但是常常会遇到离散的数据，可以用零阶保持技术（Zero-order hode technique）来将其转化成连续数据：

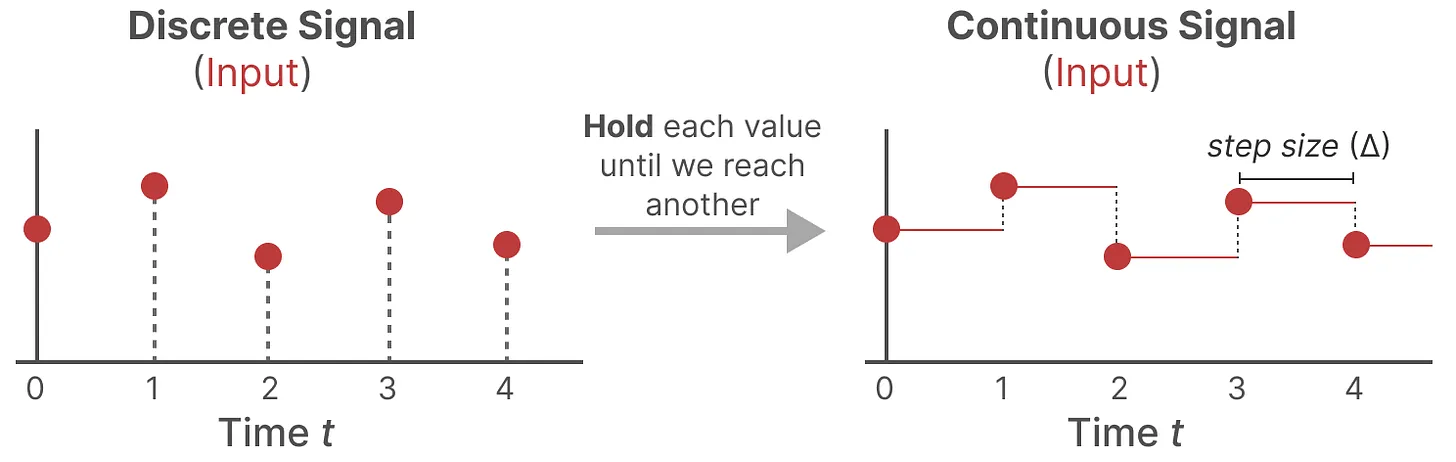
1. 首先，每次收到离散信号时，我们都会保留其值，直到收到新的离散信号，如此操作导致的结果就是创建了SSM可以使用的连续信号；
2. 保持该值的时间由一个新的可学习参数表示，称为步长(siz)——\(\Delta\)，它代表输入的阶段性保持(resolution)；
3. 有了连续的输入信号后，便可以生成连续的输出，并且仅根据输入的时间步长对值进行采样。

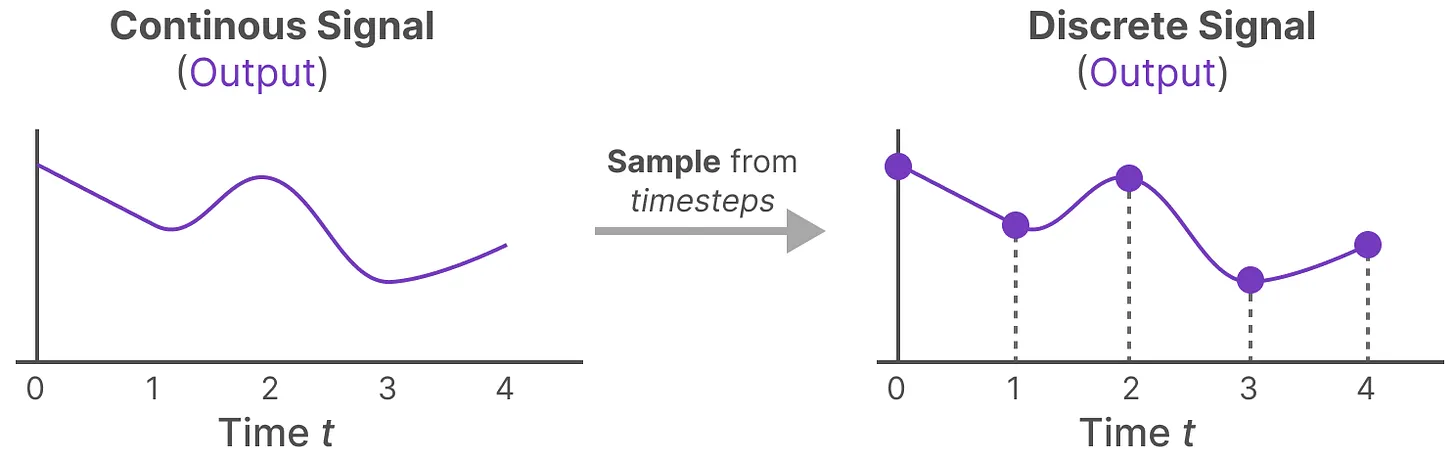
这些采样值就是我们的离散输出，且可以针对\(A,B\)按如下方式做零阶保持(做了零阶保持的在对应变量上面加了个横杠)：

\[\begin{aligned} \overline A&=\exp(\Delta A),\\ \overline B&=(\Delta A)^{-1}(\exp(\Delta A)-I)\cdot \Delta B. \end{aligned} \]

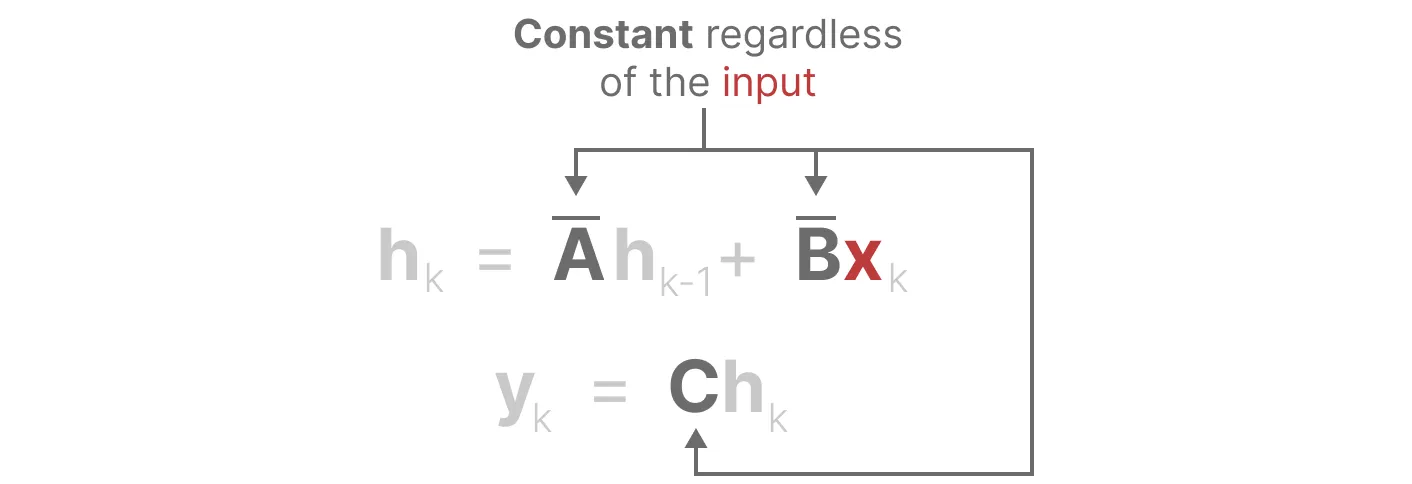
由此我们得到了SSM的循环版本：\(\begin{cases}h_k=\overline Ah_{k-1}+\overline Bx_k\\y_k=Ch_k\end{cases}\)，可以用RNN的结构来处理。

同时，我们还可以将以上版本改写成\(y_k=\left(\begin{matrix}C\overline A^k\overline B & C\overline A^{k-1}\overline B & \cdots & C\overline B\end{matrix}\right)\left(\begin{matrix}x_0\\ x_1\\ \vdots\\ x_k\end{matrix}\right)\)的形式，又由于三个参数\(\overline A,\overline B,C\)都是常数，可以使用卷积快速计算出\(\overline K=\left(\begin{matrix}C\overline A^k\overline B & C\overline A^{k-1}\overline B & \cdots & C\overline B\end{matrix}\right)\)，可以类似于CNN进行并行训练。

HiPPO

RNN的问题是隐状态的记忆能力有限，所以该怎么改善这个问题呢？

一个简单的想法是拿一个多项式拟合输入数据，而在接收到更多输入的时候，我们需要考虑如何更新这个多项式系数，那么就会有一些问题：如何找到最优的近似？如何快速的更新多项式的系数？

于是引出了HiPPO（High-order Polynomial Projection Operator）的定义：

\[A_{nk}=\begin{cases}0 & n<k;\\ n+1 & n=k;\\ 2n+1 & n>k.\end{cases} \]

具体HiPPO矩阵是如何推导出来的参见https://kexue.fm/archives/10114。

Linear Time Invariance（LTI）

由于LTI，对于SSM生成的每一个token，矩阵\(A,B,C\)都是相同的，使得其无法对输入做针对性的推理。

Mamba

与先前的研究相比，Mamba主要有三个创新点：

1. 对输入信息有选择性处理(Selection Mechanism)

2. 硬件感知的算法(Hardware-aware Algorithm)
   该算法采用“并行扫描算法”而非“卷积”来进行模型的循环计算(使得不用CNN也能并行训练)，但为了减少GPU内存层次结构中不同级别之间的IO访问，它没有具体化扩展状态
   当然，这点也是受到了S5(Simplified State Space Layers for Sequence Modeling)的启

3. 更简单的架构

   将SSM架构的设计与transformer的MLP块合并为一个块(combining the design of prior SSM architectures with the MLP block of Transformers into a single block)，来简化过去的深度序列模型架构，从而得到一个包含selective state space的架构设计

参数矩阵根据输入变化

对于几个参数矩阵进行了维度上的变化，其中\(D\)为通道数，\(L\)为数据长度，\(B\)为批量大小，因此每个批量和每个token都有一个独特不同的\(\Delta,B,C\)。

（注：\(A\)的维度为\((D,N)\)是因为在S4D中，作者将\(A\)优化成了对角矩阵，只需要对角线即可表示整个矩阵。）

同时，令\(s_B(x)=\mathrm{Linear}_N(x),s_C(x)=\mathrm{Linear}_N(x),s_\Delta(x)=\mathrm{Linear}_D(x),\tau_\Delta=\mathrm{softplus}\)来逐一将\(B,C,\Delta\)变成数据依赖化。

虽然\(A\)没有变成data dependent，但是通过SSM的离散化操作后，\((\overline A,\overline B)\)会经过outer product变成\((B,L,D,N)\)的data dependent的张量，也达到了目的。

[!NOTE]

各个变量的含义及其所谓门控之间的关系：

• \(\Delta\)类似于遗忘门

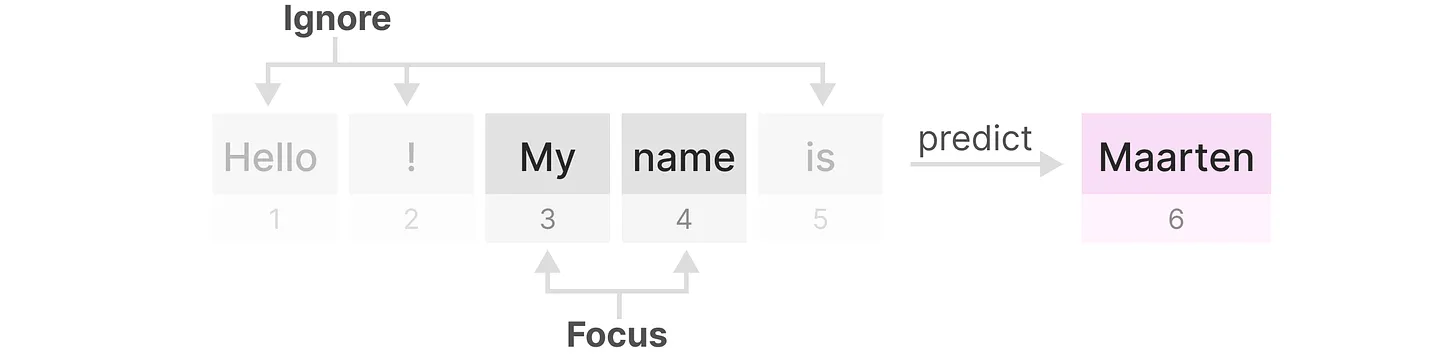
如果某个输入比较重要 它的步长就更长些，被重点关注；
如果某个输入不太重要 它的步长就短，被直接忽略。
从而对于不同的输入，达到选择性关注或忽略的目标，做到详略得当 主次分明。

• \(B\)类似于输入门，\(C\)类似于输出门

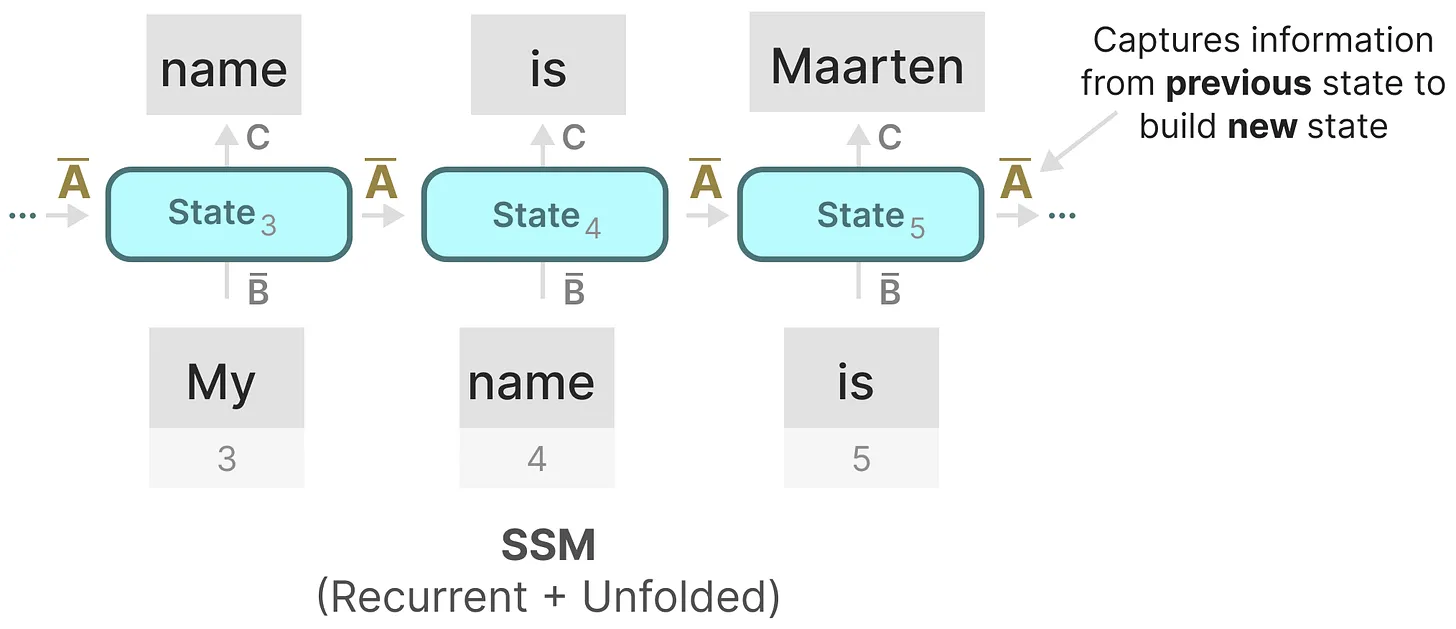
修改\(B\)和\(C\)可以允许模型更精细地控制是否让输入\(x\)进入状态\(h\)，或状态\(h\)进入输出\(y\)，所以\(B\)和\(C\)类似于RNN中的输入门和输出门。

• \(A\)意味着对应这个维度的SSM来说，A在每个hidden state维度上的作用可以不相同，起到multi-scale/fine-grained gating的作用，这也是LSTM网络里面用element-wise product的原因。

并行扫描和借鉴Flash Attention

由于\(\overline A\)现在是变化的，所以不能用并行来加速卷积的过程，但是可以用并行扫描算法使得其并行化成为可能。

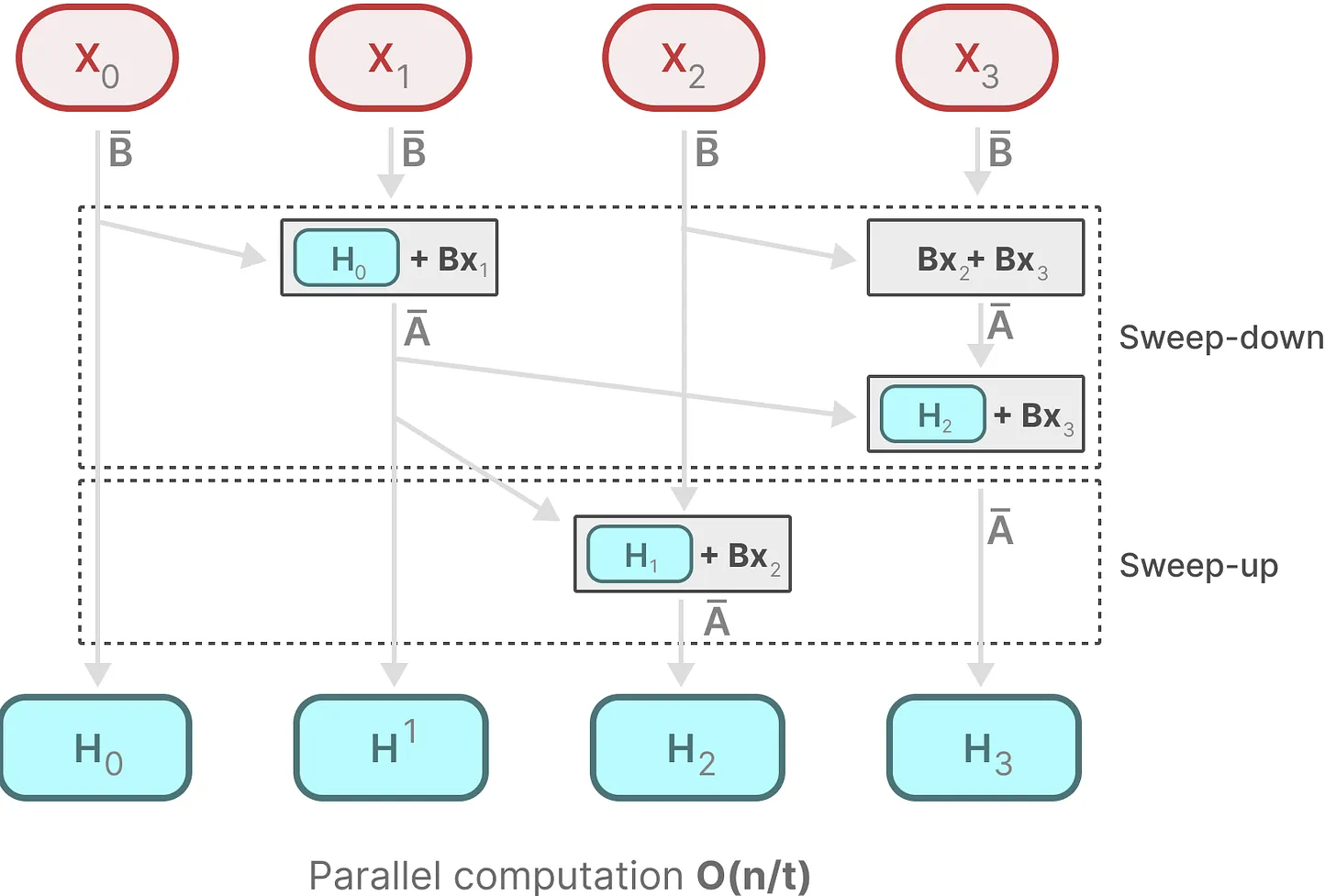
在并行计算下，时间复杂度变为\(O(n/t)\)，其中\(t\)代表用于执行任务的处理器或计算单元的数量。

此外，为了让传统的SSM在现代GPU上也能高效计算，Mamba中也使用了Flash Attention技术。

1. 简而言之，利用内存的不同层级结构处理SSM的状态，减少高带宽但慢速的HBM内存反复读写这个瓶颈；
2. 具体而言，就是限制需要从 DRAM 到 SRAM 的次数(通过内核融合kernel fusion来实现)，避免一有个结果便从SRAM写入到DRAM，而是待SRAM中有一批结果再集中写入DRAM中，从而降低来回读写的次数(更多详见：通透理解FlashAttention与FlashAttention2：全面降低显存读写、加快计算速度)

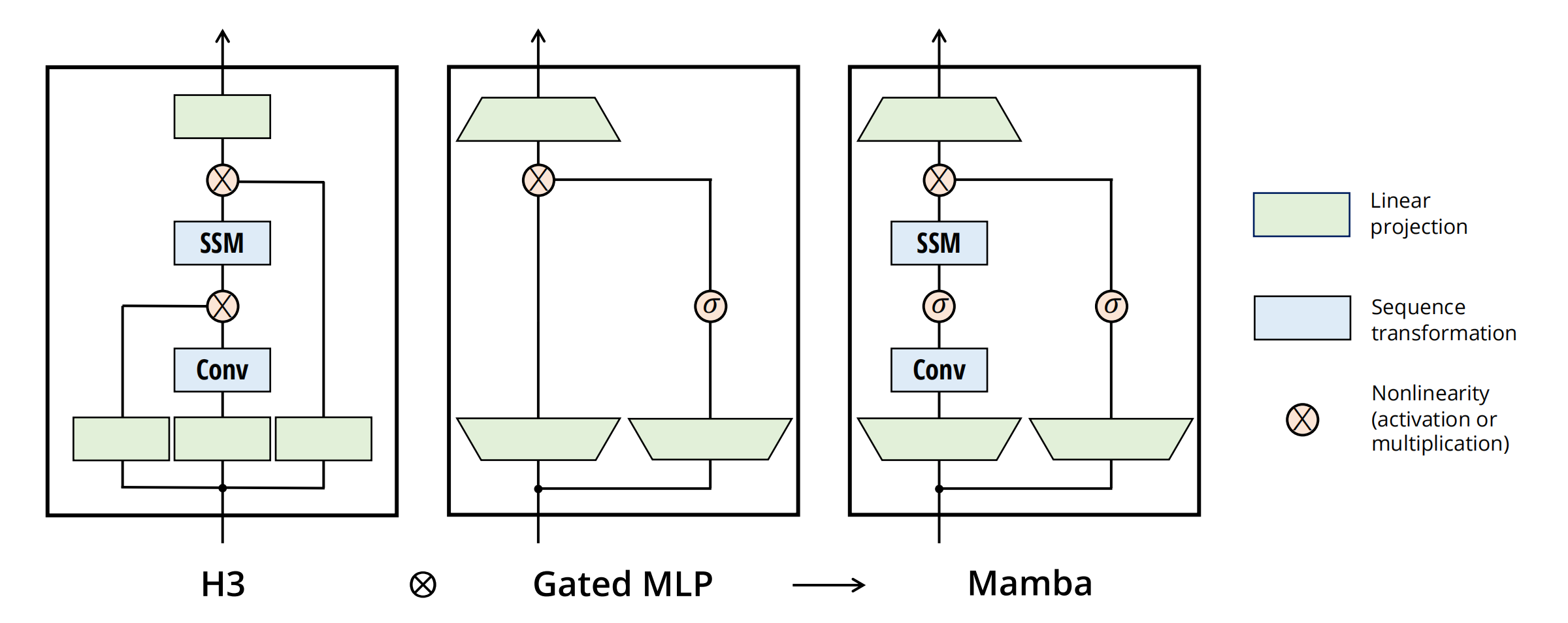
简化的SSM架构和最终的整体流程

1. 为何要做线性投影？
   经过线性投影后，输入嵌入的维度可能会增加，以便让模型能够处理更高维度的特征空间，从而捕获更细致、更复杂的特征。

2. 为什么SSM前面有个卷积？
   本质是对数据做进一步的预处理，更细节的原因在于：

   \(\rightarrow\)SSM之前的CNN负责提取局部特征(因其擅长捕捉局部的短距离特征)，而SSM则负责处理这些特征并捕捉序列数据中的长期依赖关系，两者算互为补充；
   \(\rightarrow\)CNN有助于建立token之间的局部上下文关系，从而防止独立的token计算。
   毕竟如果每个 token 独立计算，那么模型就会丢失序列中 token 之间的上下文信息。通过先进行卷积操作，可以确保在进入 SSM 之前，序列中的每个 token 已经考虑了其邻居 token 的信息。这样，模型就不会单独地处理每个 token，而是在处理时考虑了整个局部上下文。

最终在更高速的SRAM内存中执行离散化和递归操作，再将输出写回HBM，具体来说：

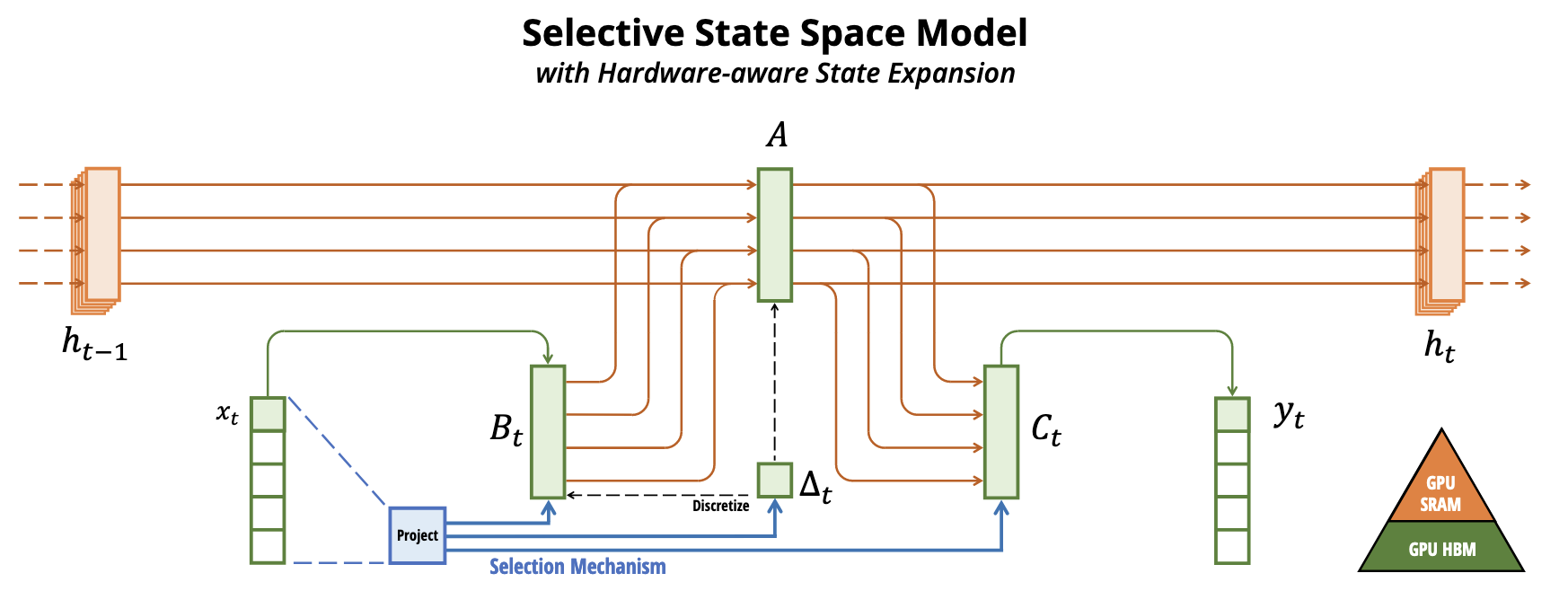
1. 不是在GPU HBM(高带宽内存)中将大小为\((B,L,D,N)\)的扫描输入进\((A,B)\)，而是直接将SSM参数\((\Delta,A,B,C)\)从慢速HBM加载到快速SRAM中；

[!CAUTION]

注意，当输入从HBM加载到SRAM时，中间状态不被保存，而是在反向传播中重新计算

2. 然后，在SRAM中进行离散化，得到\((B,L,D,N)\)的\(\overline A,\overline B\)；
3. 接着，在SRAM中进行scan(通过并行扫描算法实现并行化)，得到\((B,L,D,N)\)的输出；
4. 最后，multiply and sum with \(C\)，得到\((B,L,D)\)的最终输出写回HBM。

Phy\(\times\)Mamba（Mamba Integrated with Physics Principles Masters Long-term Chaotic System Forecasting）

Objective：对于混沌系统根据短期观测数据进行长期预报。

现有方法通常依赖长期训练数据或聚焦短期序列相关性，难以在延伸时段保持预测稳定性与动态一致性。

Preliminaries and Problem Formulation

Chaotic Dynamics. 一个混沌系统的定义是：其作为确定型动力系统，展现出对初始条件的敏感依赖，导致尽管遵循确定性规则，其在相空间内的轨迹仍以指数级分散。从形式上，可考虑由以下常微分方程（ODE）描述的一个连续时间动力系统：

\[\frac{\mathrm{d}\boldsymbol{x}(t)}{\mathrm{d}t}=\boldsymbol{f}(\boldsymbol{x}(t)), \]

其中，\(\boldsymbol{x}(t)\in\R^V\)是在时间\(t\)时的系统状态，\(V\)为系统维度，\(\boldsymbol{f}(\cdot)\)是一个控制动力的非线性向量场。混沌系统的一个标志是奇异吸引子的存在，即相空间中一个紧集\(\cal{A}\in \R^V\)，系统轨线随时间趋近于该集合，展现出复杂且非周期的行为。奇异吸引体的特征在于其分形几何结构与不变测度，二者共同刻画了系统的长期统计特性。

Lyapunov Exponent and Lyapunov Time. 李雅普诺夫指数是一组用于描述动力系统中初始邻近轨迹指数级分离率的量化指标，它们作为衡量系统混沌特性的关键参数。形式上，给定两条轨迹的初始分离向量\(\boldsymbol{\delta}_0\)，其发散程度由下式给出：

\[|\boldsymbol{\delta}(t)|\approx e^{\lambda t}|\boldsymbol{\delta}_0|, \]

其中，\(\lambda\)是李雅普诺夫指数。鉴于切向量的方向依赖性，李雅普诺夫指数呈现可变取值。其中我们重点关注最大李雅普诺夫指数（MLE），该指标是衡量系统可预测性的关键参数。通常正值最大李雅普诺夫指数表明系统处于混沌状态。最大李雅普诺夫指数定义如下：

\[\lambda_{\max}=\lim_{t\rightarrow \infty}\lim_{|\boldsymbol{\delta}_0|\rightarrow 0}\frac{1}{t}\ln\frac{|\boldsymbol{\delta}(t)|}{|\boldsymbol{\delta}_0|}, \]

其中\(|\boldsymbol\delta_0|\rightarrow0\)保证线性逼近的适用性始终成立。李雅普诺夫时间定义为最大李雅普诺夫指数（MLE）的倒数，即\(T_L = 1/λ_{\max}\)，表征动力系统呈现混沌特性的特征时间尺度。

Problem Formulation. 给定一个包含\(T\)个时间步长的历史观测窗口，记为\(\{x(t)\}_{t=1}^T\)，我们的目标是有效预测系统未来尽可能长的\(H\)个步长的状态\(\{\hat x(t)\}_{t=T+1}^{T+H}\)，其中\(T\ll H\)。预测任务涉及两个关键目标：(1) 实现精确的点序列预测，即对于所有\(t\in[T+1, T+H]\)，满足\(\hat x(t) \approx x(t)\)；(2) 保持系统固有的动力学特性，例如奇异吸引子的几何结构及关键统计不变量。由于混沌系统的敏感性，当精确状态预测超出多个李雅普诺夫时间范围后变得愈发困难时，后者的重要性就日益凸显。具体评估指标后续会提到。

Methods

Attractor Manifold Reconstruction via Time-delay Embedding

High-dimensional representation for chaotic systems: 给定来自混沌系统吸引子的单变量轨迹\(\boldsymbol{x}\in\R^T\)（包含\(T\)个观测步点），我们定义两个超参数：嵌入维度\(m\)和时延\(\tau\)，并按以下方式构建高维轨迹：

\[\boldsymbol{z}_t=(\boldsymbol{x}_{t-(m-1)\tau},\boldsymbol{x}_{t-(m-2)\tau},\cdots,\boldsymbol{x}_t)\in\R^m, \]

其中，\(m\)代表嵌入维度，\(\tau\)代表延迟时间步长，这里通过互信息（AMI）和虚假最近邻（FNN）方法来选择它们。Takens嵌入定理证明，通过单维观测序列的时滞嵌入重构，我们能够还原该高维系统吸引子的流形结构。我们将不同变量的组合表示法定义为\(\boldsymbol{Z}\in\R^{V\times T\times m}\)，其中\(V\)是系统本身的维度。

Patching and tokenization: 为探究混沌系统动态特性，必须捕捉观测数据中跨时间步长的时间相关性。对于一个物理信息表征\(\boldsymbol{Z}\in\R^{V\times T\times m}\)，我们把它划分成\(N=\lfloor\frac{T}{D}\rfloor\)个相互不重叠，且大小为\(D\)的块\(\boldsymbol{P}\in\R^{N\times(D\times T\times m)}\)，接下来，将每一个\(\boldsymbol{P}_i\)线形映射到一个\(d\)维的token \(\boldsymbol{S}_i\)：

\[\boldsymbol{S}_i=\boldsymbol{W}_\text{token}\boldsymbol{P}_i+\boldsymbol{b}_\text{token}, \]

其中，\(\boldsymbol{W}_\text{token},\boldsymbol{b}_\text{token}\)是可学习参数。因此，输入的token序列可以被表示为\(\boldsymbol{S}=\{\boldsymbol{S}_i\}_{i=1}^N\)，其中\(\boldsymbol{S}_i\in\R^d\)。

Benefits：促进局部化时间模式的提取，实现对其长期行为的稳健预测，优化模型的可扩展性。

Decomposed Forecasting with Generative Mamba

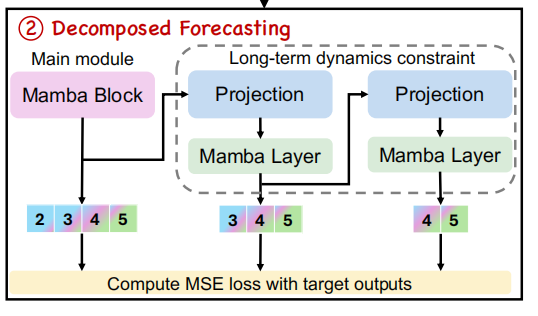
使用了一个生成训练策略来使得模型能够自回归的预测下一个token：

\[P(\boldsymbol{S})=\prod_{i=1}^N p(\boldsymbol{S}_i|\boldsymbol{S}_{<i}), \]

其中\(\boldsymbol{S}\)和\(N\)分别代表token序列和对应的序列长度。使用了一堆Mamba层来执行上式。对于第\(l\)个Mamba层，我们有：

\[\mathbf{h}_i^{(l)}=\mathrm{Mamba}^{(l)}(\mathbf{r}_i^{(l-1)}),\ \ \ \ \ \widehat{\boldsymbol{S}}_{i+1}^{(l)}=\mathrm{Decoder}(\mathbf{h}_i^{(l)}),\ \ \ \ \ \mathbf{r}_i^{(l)}=\mathbf{r}_{i}^{(l-1)}-\boldsymbol{S}_{i+1}^{(l)}, \]

其中，\(\mathbf{r}_i^{(l)}\)表示在第\(l\)层的残差，\(\mathbf{r}_i^{(0)}=\boldsymbol{S}_i\)，解码器通过线性层实现，预测的下一个token \(\widehat{\boldsymbol{S}}_{i+1}=\sum\limits_{l=1}^L\widehat{\boldsymbol{S}}_{i+1}^{(l)}\)，其中\(L\)代表在残差堆叠架构中Mamba层的数量。

另外，应用了\(M\)个辅助模型来预测\(M\)个子序列token。每一个MTP（multi-token prediction）模型包含一个专门的Mamba层，和一个融合投射（fusion projection）层\(\psi(\cdot)\)。在预测第\(i\)个token的第\(m\)个深度时，模型通过融合投射合并了预测深度为\(m-1\)的隐表达\(\mathbf{v}_i^{m-1}\in\R^d\)和第\(i+m\)个token的嵌入\(\boldsymbol{S}_{i+m}\in\R^d\)：

\[\mathbf{v}_i^{m'}=\psi([\mathrm{RMSNorm}(\mathbf{v}_i^{m-1}),\boldsymbol{S}_{i+m}]), \]

其中\(\mathrm{RMSNorm}\)层是为了标准化，\([\cdot,\cdot]\)代表连接操作，\(\mathbf{v}_i^1=\sum\limits_{l=1}^L\mathbf{h}_{i-1}^{(l)}\)。\(\mathbf{v}_i^{m'}\)接着通过对应的MTP模型的Mamba层，来生成更新的表达\(\mathbf{v}_i^m\)。接下来，\(\mathbf{v}_i^m\)被用来预测第\(m\)个未来的token：

\[\mathbf{v}_{1:N-m}^m=\mathrm{Mamba}(\mathbf{v}_{1:N-m}^{m'}),\ \ \ \ \ \widehat{\boldsymbol{S}}_{i+m+1}^m=\phi(\mathbf{v}_i^m), \]

其中\(N\)表示输入序列的长度。

因此生成训练的目标包括next-token和multi-token prediction，可以表示为：

\[{\cal L}={\cal L}_\text{next}+\frac{\lambda_p}{M}\sum_{m=1}^M{\cal L}_\text{MTP}^m, \]

其中\(\lambda_p\)代表MTP目标的相对权重，\({\cal L}_\text{next},{\cal L}_\text{MTP}^m\)依照teacher forcing strategy执行：

\[{\cal L}_\text{next}=\frac{1}{NB}\sum_{b=1}^B\sum_{i=2}^N||\boldsymbol{S}_i-\widehat{\boldsymbol{S}}_i||^2,\ \ \ \ \ {\cal L}_\text{MTP}^m=\frac{1}{(T-1+m)B}\sum_{b=1}^B\sum_{i=2+m}^T||\boldsymbol{S}_i-\widehat{\boldsymbol{S}}_i^m||, \]

其中\(B\)代表一个batch中的训练样本。

multi-token prediction模型只在训练阶段使用，推理阶段只依赖于main Mamba block来自回归预测。

Attractor Geometry Preservation via Distribution Matching

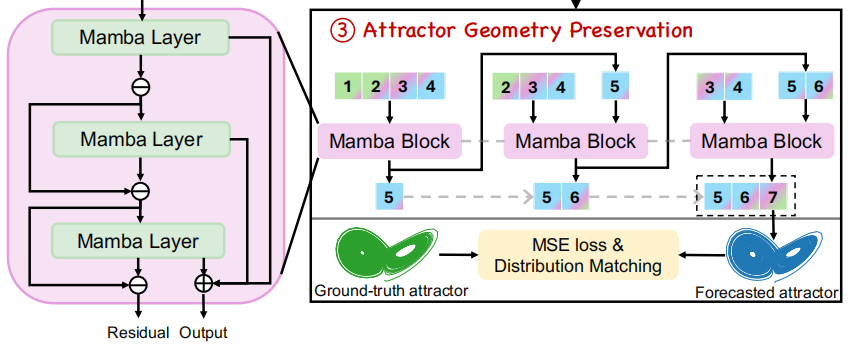
teacher forcing strategy会导致模型过于依赖真实token，从而与推断时的自回归特性产生不一致，并可能导致其在长时序预测任务上的性能下降。

介绍了一个额外的student-forcing训练阶段，其中模型根据历史预测自回归的生成\(W\) token，并且计算MSE loss：

\[{\cal L}_\text{stu}=\frac{1}{WB}\sum_{b=1}^B\sum_{j=1}^W||\boldsymbol{S}_j-\widehat{\boldsymbol{S}}_j||^2. \]

此外，既往研究已证明：在训练目标中显式引入长期系统统计特征作为物理约束正则化项，能显著提升混沌系统在较长预测期的预报精度。

假设\(\{\boldsymbol{u}^{(i)}\}_{i=1}^n\sim p_1,\{\boldsymbol{v}^{(i)}\}_{i=1}^n\sim p_2\)是两个分别从\(p_1,p_2\)中取样，大小为\(n\)的轨迹，MMD（Maximum Mean Discrepancy）的估算可以被写成：

\[\widehat{\text{MMD}}^2=\frac{1}{n^2}\sum_{i,j}\kappa(\boldsymbol{u}^{(i)},\boldsymbol{u}^{(j)})+\frac{1}{n^2}\sum_{i,j}\kappa(\boldsymbol{v}^{(i)},\boldsymbol{v}^{(j)})-\frac{2}{n^2}\sum_{i,j}\kappa(\boldsymbol{u}^{(i)},\boldsymbol{v}^{(j)}). \]

我们将\(\kappa\)作为有理二次核的混合核。由于所有的轨迹都源于相同的吸引子，预测出来的轨迹的统计学分布\(\hat p\)理论上应该与观测轨迹中得到的\(p^*\)和真实未来轨迹中得到的\(p\)一致。所以正则化项可以被定义为：

\[{\cal L}_\text{reg}=\widehat{\text{MMD}}^2(p^*,\hat{p})+\lambda_c\widehat{\text{MMD}}^2(p,\hat{p}), \]

其中，\(\lambda_c\)是一个控制两个正则化项相对权重的超参数。所以student forcing部分的最终损失函数\({\cal L}={\cal L}_\text{stu}+\lambda_r{\cal L}_\text{reg}\)，其中\(\lambda_r\)是相对权重。

Pangu（Accurate medium-range global weather forecasting with 3D neural networks）

technical contribution:

• 将高度信息融入新维度，从而使深度神经网络的输入和输出可以在三维空间中被概念化;
• 采用了一种分层时间聚合算法，该算法涉及训练预测提前期逐步增加的系列模型。

3DEST（3D Earth-specific Transformer）

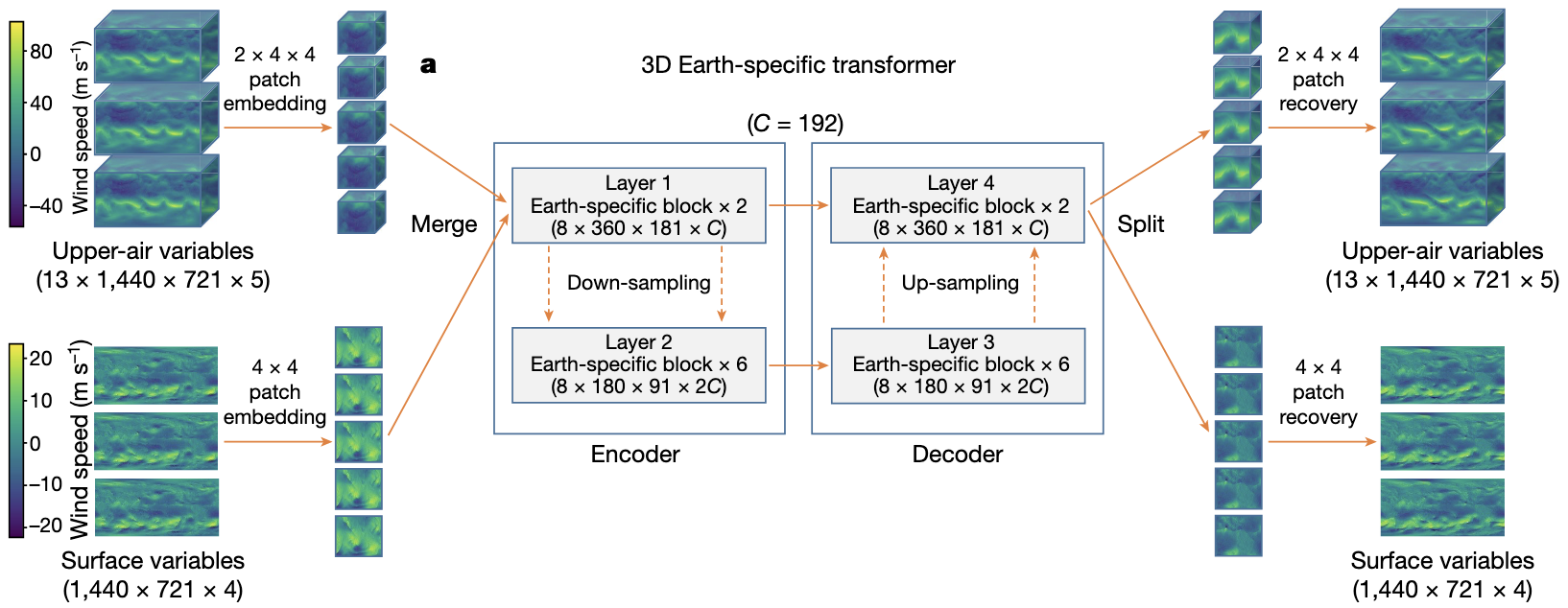
这是一个vision transformer的变种，输入和输出都是在特定时间点的三维气象数据。

对于一个模型来说，输入和输出之间的lead time是固定的，因此需要通过聚合不同lead time的多模型实现即时天气预报。

有两种输入：高空变量和地表变量。前者有13个气压层，构成\(13\times 1440\times 721\times 5\)的数据矩阵；后者是一个\(1440\times 721\times 4\)的数据矩阵。

Patch embedding and patch recovery

使用patch embedding将这些数据映射到一个\(C\)维的隐空间，高空变量使用\(2\times4\times4\)的patch大小，得到\(7\times360\times181\times C\)的数据矩阵，地表变量使用\(4\times4\)的patch大小，得到\(360\times181\times C\)的数据矩阵，再将两者按第一维连接起来，得到\(8\times360\times181\times C\)的矩阵。

patch embedding使用了线形层和GeLU激活函数。

The encoder-decoder architecture

接下来这个矩阵被传到一个标准的encoder-decoder结构，其中有8个encoder层和8个decoder层。对于前2个encoder层，形状保持不变，在接下来的6个encoder层中，水平维度减少了一半，并且通道数变成了两倍，形状变成了\(8\times180\times91\times 2C\)。decoder层和encoder层是对称的，前6个decoder层的大小为\(8\times180\times91\times 2C\)，后2个的大小为\(8\times360\times181\times C\)。

¿The outputs of the 2nd encoder layer and the 7th decoder layer are concatenated along the channel dimension.?

对于down-sampling，我们将4个token合并成一个，这样通道数从\(C\)变成了\(4C\)，然后通过一个线形层，将通道数变成\(2C\)，up-sampling的操作相反。

3D Earth-specific transformer blocks

每一个encoder-decoder层都是一个3DEST（3D Earth-specific transformer）block，类似于标准vision transformer block。为了进一步减少计算代价，我们继承了window-attention mechanism来将特征矩阵（\(8\times360\times181\)或\(8\times180\times91\)）分割成窗口，每一个窗口包含\(2\times12\times6\)个token，标准self-attention mechanism被应用在每个窗口中：

\[\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{SoftMax}(\mathbf{QK}^\top/\sqrt{D}+\mathbf{B})\mathbf{V}. \]

Earth-specific positional bias

与swin transformer不同，每一个token代表的是地球上的绝对位置，所以相邻token间的位置关系不同；并且一些气象状态与绝对位置息息相关。为了抓住这些特点，我们使用了Earth-specific positional bias，\(\mathbf{B}_\mathrm{ESP}\)。

具体的，令总的特征矩阵有\(N_\mathrm{pl}\times N_\mathrm{lat}\times N_\mathrm{lon}\)的空间分辨率，swin transformer这些分割成\(M_\mathrm{pl}\times M_\mathrm{lat}\times M_\mathrm{lon}\)个窗口，每个窗口的大小为\(W_\mathrm{pl}\times W_\mathrm{lat}\times W_\mathrm{lon}\)，Earth-specific positional bias矩阵包含\(M_\mathrm{pl}\times M_\mathrm{lat}\)个子矩阵（因为经度的下标是循环的，而且是均匀分布的，所以不同经度共享相同的bias），每个包含\(W_\mathrm{pl}^2\times W_\mathrm{lat}^2\times (2W_\mathrm{lon}-1)\)个可学习的参数。

Hierarchical temporal aggregation

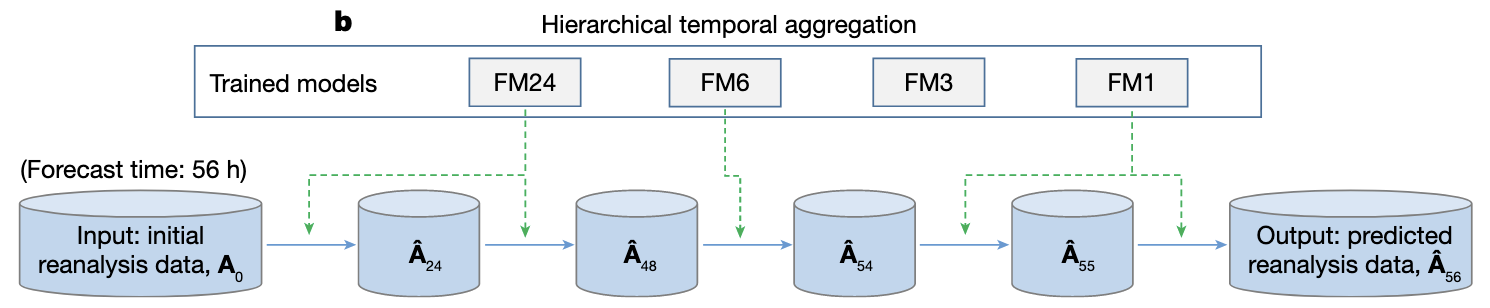
This prompted us to call the base deep networks (lead times being 1 h, 3 h, 6 h or 24 h) iteratively, using each forecasted result as the input of the next step. To reduce the cumulative forecast errors, we introduced hierarchical temporal aggregation, a greedy algorithm that always calls for the deep network with the largest affordable lead time.!