树上科技

1. 树的直径

树上任意两节点之间最长的简单路径即为树的「直径」。

1.1 两次 DFS

从树的任意一点 \(x\) 出发，找到距离 \(x\) 最远的节点 \(y\)，随后再从 \(y\) 出发，找到离 \(y\) 最远的节点 \(z\)，则 \(y\rightarrow z\) 即为树的一条直径。

证明考虑使用反证法。令 \(d(s,t)\) 表示真实直径，\(x\) 第一次出发到达点 \(y\)（\(y\ne s,t\)），分三类讨论：

1. \(x\) 在 \(s\rightarrow t\) 路径上。则 \(d(x,y)>d(x,t)\Rightarrow d(s,y)>d(s,t)\)，与直径定义矛盾。

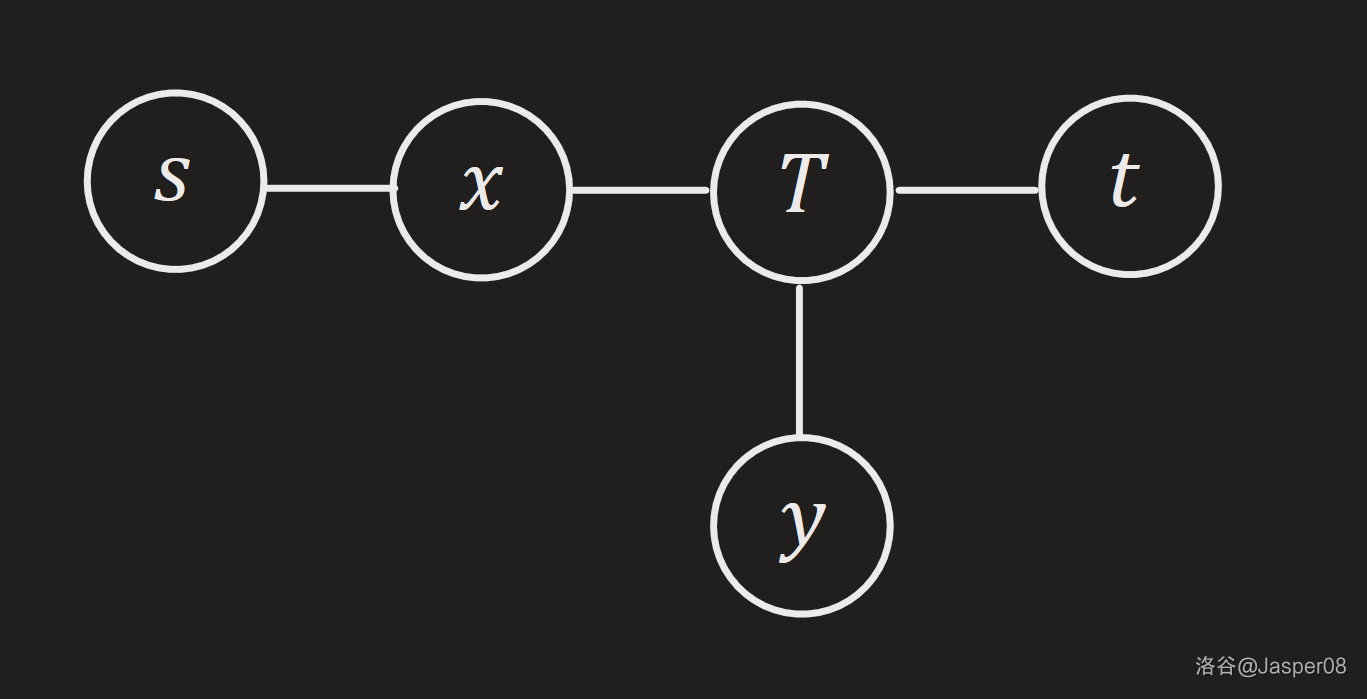
2. \(x\) 不在\(s\rightarrow t\) 路径上，且 \(x\rightarrow y\) 与 \(s\rightarrow t\) 有重合路径。不妨设第一个重合的点为 \(z\)。则 \(d(x,y)>d(x,t)\Rightarrow d(z,y)>d(z,t)\Rightarrow d(s,y)>d(s,t)\)，与直径定义矛盾。

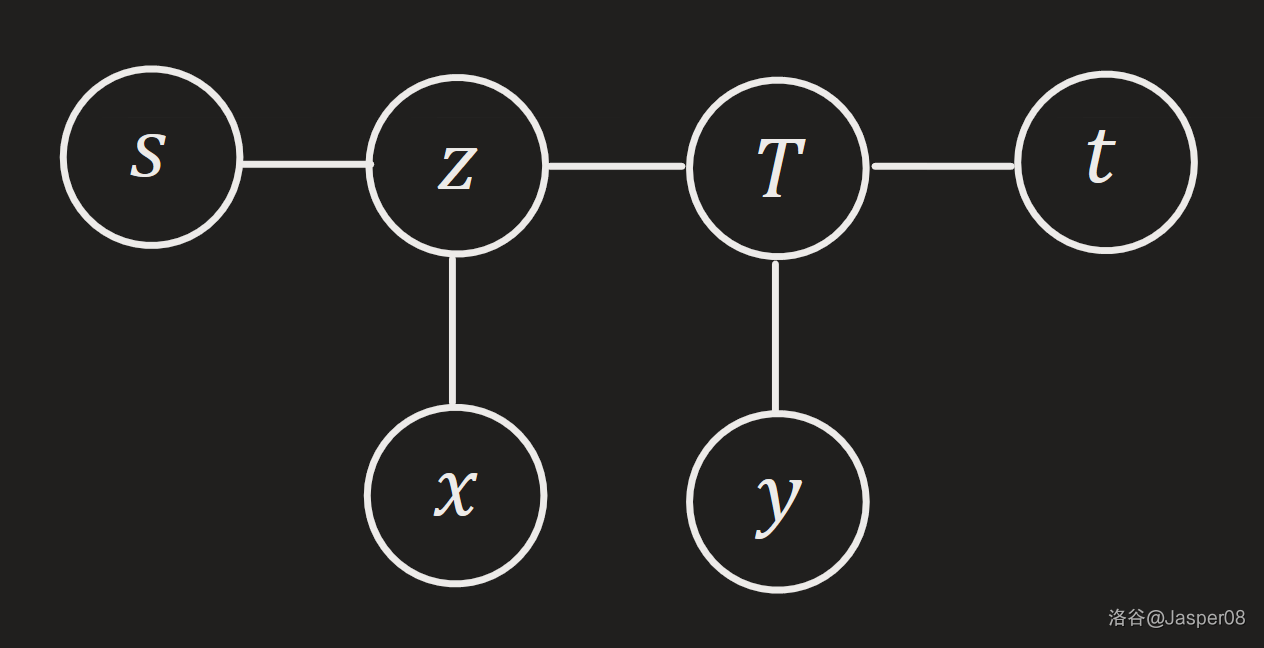
3. \(x\) 不在\(s\rightarrow t\) 路径上，且 \(x\rightarrow y\) 与 \(s\rightarrow t\) 无重合路径。则 \(d(x,y)>d(x,t)\Rightarrow d(T,y)>d(T,t)\Rightarrow d(s,y)>d(s,t)\)，与直径定义矛盾。

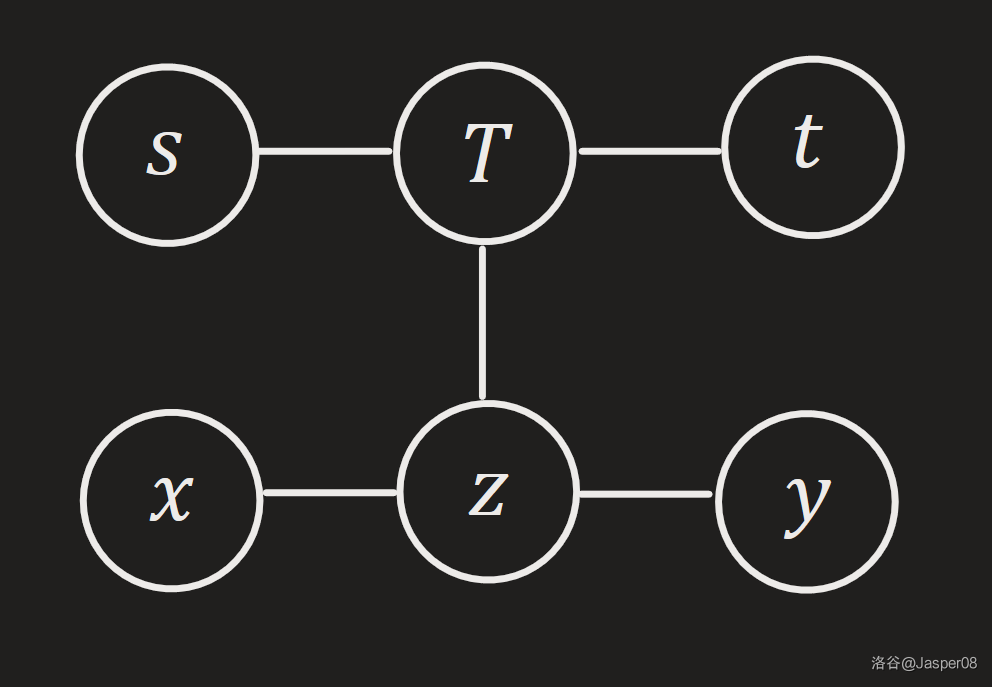
综上，原定理得证。

需要注意的是，两次 dfs/bfs 不能求解有负权边的情况。

1.2 树形 dp

对于一点 \(u\)，通过 dfs 求出其向下的最长路径 \(d_1\) 和次长路径 \(d_2\)，则以 \(u\) 为路径上一点，且所有点的深度大于 \(u\) 的最长路径长度为 \(f_u=d_1+d_2\)。

树的直径长为 \(\max_{1\le i\le n} f_i\)。

树形 dp 可以求解有负权边的情况。

2. LCA

两个节点的最近公共祖先（LCA），就是这两个点的公共祖先里面，离根最远的那个。

2.1 RMQ LCA

首先要了解欧拉序列：

对一棵树进行 DFS，无论是第一次访问还是回溯，每次到达一个节点时都将编号记录下来，得到一个长度为 \(2n-1\) 的序列，则这个序列被称作树的欧拉序。

令 \(u\) 在欧拉序中第一次出现的位置为 \(pos(u)\)，\(E\) 表示树的欧拉序。那么，\(pos(\text{lca}(u,v))=\min\{E_{pos(u)},\cdots,E_{pos(v)}\}\)。

这个式子可以这样理解：由于从 \(u\) 走到 \(v\) 的路径中一定会经过 \(\text{lca}(u,v)\)，但不会经过 \(\text{lca}(u,v)\) 的祖先。因此，从 \(u\) 到 \(v\) 的过程中经过的欧拉序最小的节点就是 \(\text{lca}(u,v)\)。

预处理 \(O(n\log n)\)，查询 \(O(1)\)，不支持修改。

P3379 【模板】最近公共祖先（LCA）

点击查看代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>

using namespace std;

const int N = 5e5+10;

int n, m, s;
vector<int> e[N];
int st[2*N][25], pos[N], dfn[N*2], idx;

void dfs(int u, int fa) {
	dfn[++ idx] = u, pos[u] = idx;
	for (auto v : e[u]) {
		if (v == fa) continue;
		dfs(v, u);
		dfn[++ idx] = u;
	}
}

int Min(int x, int y) {
	return (pos[x] < pos[y]) ? x : y;
}

void init() {
	for (int i = 1; i <= idx; ++i) st[i][0] = dfn[i];
	for (int i = 1; i <= ceil(log2(idx)); ++i) {
		for (int j = 1; j <= idx-(1<<i)+1; ++j) 
			st[j][i] = Min(st[j][i-1], st[j+(1<<i-1)][i-1]);
	}
}

int query(int l, int r) {
	if (l > r) swap(l, r);
	int k = log2(r-l+1);
	return Min(st[l][k], st[r-(1<<k)+1][k]);
}

int lca(int u, int v) {
	u = pos[u], v = pos[v];
	return query(u, v);
}

int main() {
	scanf("%d%d%d", &n, &m, &s);
	
	int x, y;
	for (int i = 1; i < n; ++i) {
		scanf("%d%d", &x, &y);
		e[x].push_back(y), e[y].push_back(x);
	}
	
	dfs(s, -1);
	init();
		
	while (m -- ) {
		scanf("%d%d", &x, &y);
		printf("%d\n", lca(x, y));
	}
	return 0;
} 

2.2 倍增 LCA

令 \(f(x,i)\) 表示 \(x\) 的第 \(2^i\) 个祖先，则 \(f(x,i+1)=f(f(x,i),i)\)。查询时，令 \(d\) 表示 \(u,v\) 两点的深度之差，从 \(d\) 的最高二进制位开始尝试，若 \(f(u,i)\ne f(v,i)\)，则 \(u\leftarrow f(u,i),v\leftarrow f(v,i)\)，最后得到 LCA 为 \(f(u,0)\)。

预处理 \(O(n\log n)\)，查询 \(O(\log n)\)，同时可以计算距离。

3. 基环树

基环树是一个 \(n\) 个点 \(n\) 条边的连通无向图（或有向图）。若不保证联通，则为基环树森林。一个基环树中有且仅有一个环。

对于基环树上的问题，通常采用断环成链的方式解决。