202212_QQ群_e与phi_n不互素
Tags:e与phi_n不互素
0x00. 题目
p = 157530675441878626599464138715487200701326841355123090483347798840045775145949014618812159707477136917984099110403212184519370802642618127967374460666077425009171534283832790679736888366422651836381366696006619080355876127198155674381637654984256558647577445423495989734771254937503088247853356995710950180277
q = 139829892814776911217064733367611300206100548995118676801497574968358144072518974860699361640054273694659411369508474259763772175594751524806585560899013298570753062340345963558344542565031641001600097876512629128365230485168095526956443633356945391798820105691601758392840648438128151033074967026443243504817
c = 19578459378627606199477079053036270159563881059438281387193040788826945649491485563897734181744375515028092148531799469835307242105157535333720976173194557385360193094260638155771535336927076068219288963163434042359549174121570095459591043161803276364650465203984742536551192087165491408459375686814573687928891634714882667397874225023076240590384109329732273447737516123620118504848631137324054667472576983647315886488226968053613328102730752046006838386364213547717326295238566955059403922121289555337918515313495110885681380019305209026639707269438024875746063720961174837562089244451855653520578986635635684269681
e = 570
0x01. WP
如果GCD(e,phi_n)较小,可直接用e//_gcd解密后再开_gcd次根
\[\begin{equation}\begin{split}
m^e \quad mod \quad N &= m^{(e//\_gcd)*\_gcd} \quad mod \quad N \\
&= (m^{\_gcd})^{e//\_gcd}\quad mod \quad N
\end{split}\end{equation}
\]
exp.py
from Crypto.Util.number import *
import gmpy2
p = 157530675441878626599464138715487200701326841355123090483347798840045775145949014618812159707477136917984099110403212184519370802642618127967374460666077425009171534283832790679736888366422651836381366696006619080355876127198155674381637654984256558647577445423495989734771254937503088247853356995710950180277
q = 139829892814776911217064733367611300206100548995118676801497574968358144072518974860699361640054273694659411369508474259763772175594751524806585560899013298570753062340345963558344542565031641001600097876512629128365230485168095526956443633356945391798820105691601758392840648438128151033074967026443243504817
c = 19578459378627606199477079053036270159563881059438281387193040788826945649491485563897734181744375515028092148531799469835307242105157535333720976173194557385360193094260638155771535336927076068219288963163434042359549174121570095459591043161803276364650465203984742536551192087165491408459375686814573687928891634714882667397874225023076240590384109329732273447737516123620118504848631137324054667472576983647315886488226968053613328102730752046006838386364213547717326295238566955059403922121289555337918515313495110885681380019305209026639707269438024875746063720961174837562089244451855653520578986635635684269681
e = 570
n = p * q
phi_n = ( p - 1 ) * (q - 1 )
_gcd = GCD(e, phi_n)
print('_gcd=',_gcd)
# _gcd=6比较小,直接iroot开e//_gcd次根
d = inverse(e//_gcd, phi_n)
m_gcd = pow(c, d, n)
m = gmpy2.iroot(m_gcd, _gcd)
# 得到元组(mpz(38321129010637881541398039502744968622249664469689725), True)
flag = long_to_bytes(int(m[0]))
print(flag)
# b'flag{JChan_Visit_Here}'
或直接使用工具
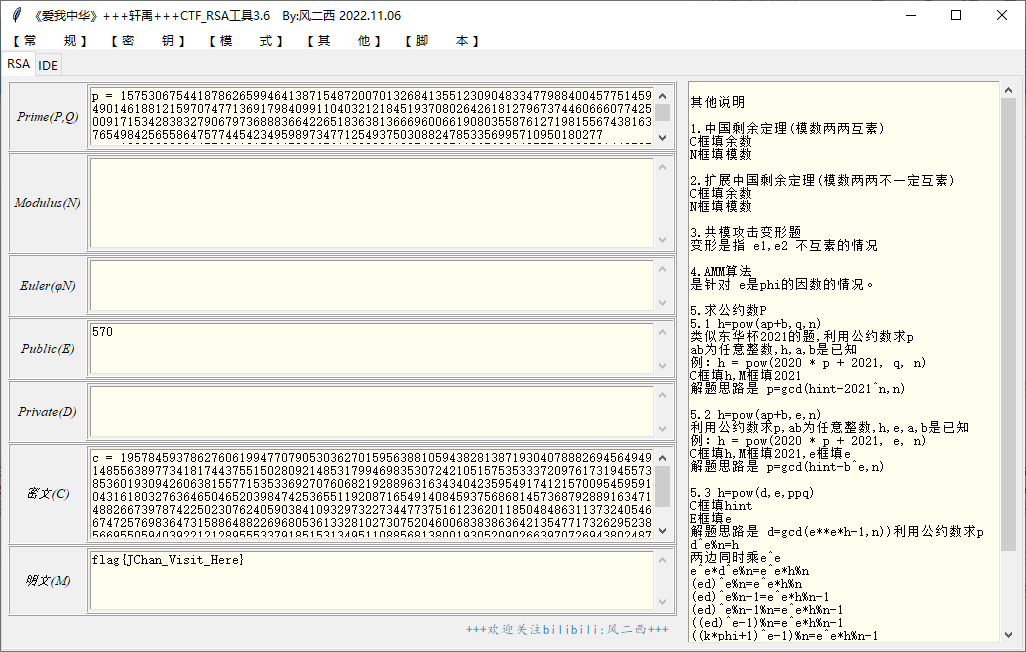


 RSA,e与phi_n不互素
RSA,e与phi_n不互素

 浙公网安备 33010602011771号
浙公网安备 33010602011771号