哈希表

哈希表

一、背景

在对数据的日常处理中，查找是一项基本操作。通常，查找算法都是基于对比的，比如在一条链表中有n个节点，要找到其中的某个节点，最基本的思路就是从头到尾依次遍历每个节点，依次对比每个节点是否是想要的节点，这样的查找方式，称为顺序查找。

很显然，顺序查找并不会给查找效率带来任何惊喜，其时间复杂度是O(n)

提高查找效率的办法有很多，比如可以将这些数据按照二叉搜索树的逻辑结构组织起来，那么从根部开始查找某节点的时间复杂度就变成O(log₂n)，又或者使用顺序存储并将节点排序，那么每次查找可以从中间开始，进行折半查找，时间复杂度也是O(log₂n)。

不管是顺序查找，还是改良后的BST、折半算法，查找一个节点都需要花一定的时间，之所以要花时间是因为存储节点的时候，节点的位置与节点的字段（姓名、学号、成绩...）之间没有对应关系，因此我们需要一个个比对每一个节点，上述算法的差异只是改变了比对的规则，使得效率提高，但仍然是一个一个比对的过程。如果查找节点不需要比对，那就可以节省大量的时间。

二、哈希表

为了避免节点比对，我们可以在存储节点的时候，让节点的位置和节点本身做一个映射关系(比如根据学号计算得到该同学的宿舍号)，这样一来就可以直接根据节点本身的特征值计算得到节点的位置了，注意：此时节点的位置不是"找"出来的，而是计算出来的。

这种存储数据的方式，被称为哈希表（Hash Table），也被称为散列表。时间复杂度是O(1)，即查找任何一个数据理论上不需要时间，直接给出数据所在的位置。

1. 基本概念

哈希表的思路简单易懂，将相关的概念陈述如下：

键（Key）：即用来作为节点特征的字段。比如学生的姓名、分数、学号（可以是数据中的任何一个成员）等。
值（Value）：节点存储的位置，也被称为哈希地址（数组下标）。
哈希函数（Hash Function）：将键转换为值的映射关系（计算公式下标 = HashFunc(键)）。
冲突（Conflict）：当不同键的键映射到相同的值时，称为冲突。

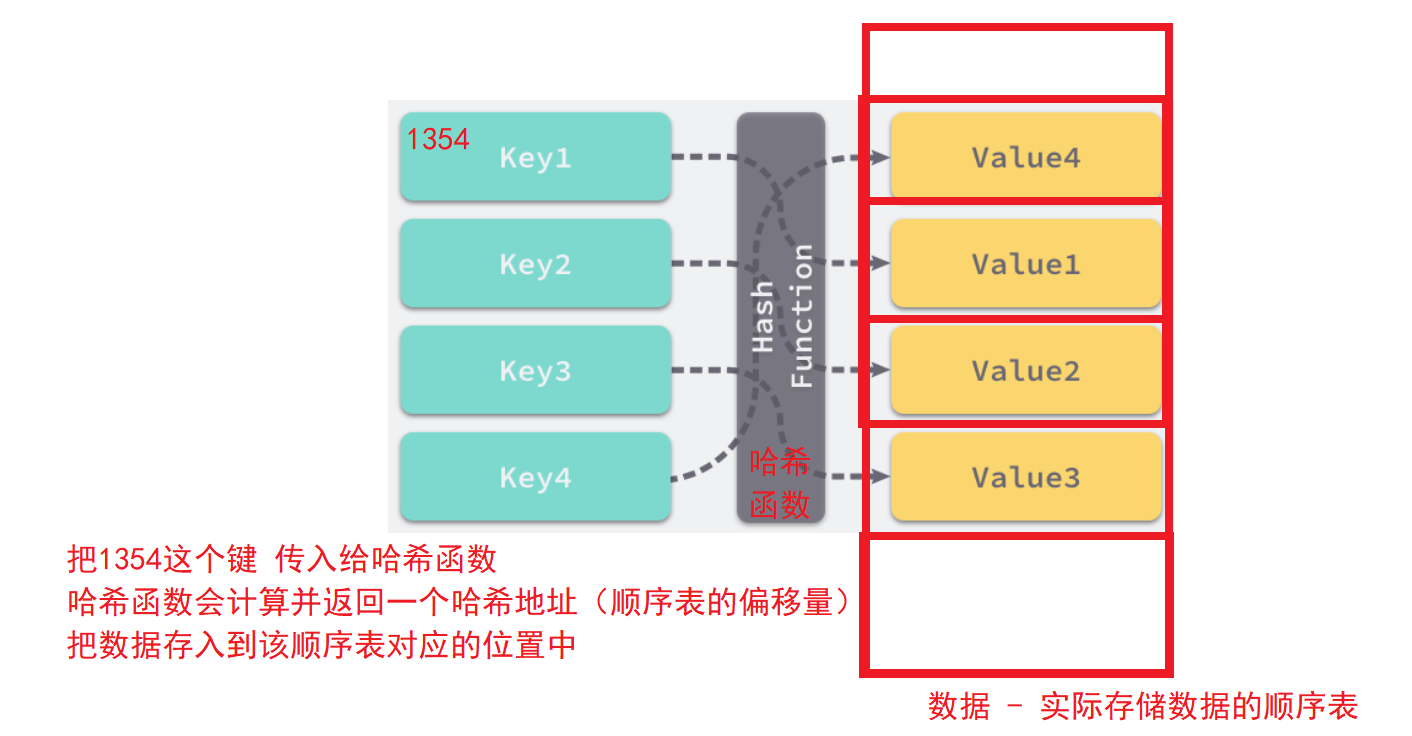
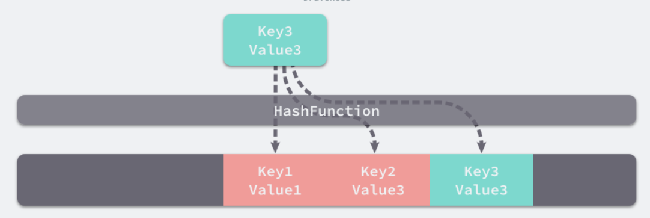
如上图所示，所谓的哈希存储就是将键映射为哈希地址，存入右侧的某个空位中。右侧实际上是一个数组或顺序表，所谓的哈希地址一般指的是数组的下标，哈希表一般指的是该数组。

哈希表主要就是解决两件事情：

确定一个哈希函数
解决可能会出现的冲突问题

2. 哈希函数

将节点某字段（即键）转换为哈希地址（值）的过程，就是哈希映射。举个例子，假设要将班级里的学生用哈希表的方式来存储，将姓名作为键，可以有如下哈希映射：

将姓名笔画数，作为节点的哈希地址。

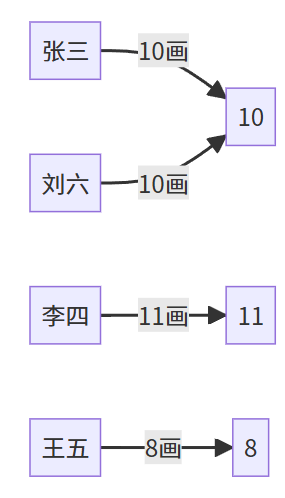
从上面的例子可以看到，以笔画数作为映射规则是很不理想的，因为大多数人的姓名笔画数都集中在10-20之间，这不利于将各个元素均匀地分布在哈希表中，并且这种算法很容易有冲突。

哈希函数的选取没有一定之规，但一个大的原则是：尽量充分地使用键的信息，尽量使得值均匀分布。符合这个大原则的其中一种哈希函数，称为除留余数法，即：将键对不大于哈希表长度的最大质数求余，将其结果作为哈希地址。

以上面学生为例，假设班级中学生人数在50人左右，将哈希表数组的长度定为50，那么哈希函数可以是：

H(key) = key % 47**

此处，47是不大于50的最大的质数，之所以不能大于50，是因为哈希地址最终是数组的下标，如果比数组的长度还大的话就可能会越界。选取质数则有利于值域分布更加均匀。另外，为了让数据分布更加均匀，可以使用姓名拼音的ASCII码之和来作为键。

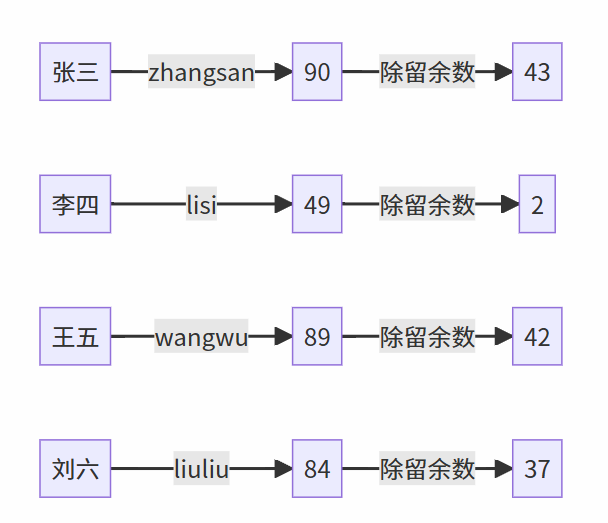
可见，经过对哈希函数的改良，使得哈希地址分布更加均匀了，冲突概率也降低了。但从另一方面讲，冲突就像物理实验中的误差，可以被降低，但很多时候无法根除，比如上述例子，假如现在入学一位名字为马化腾的学生，那么将会出现：

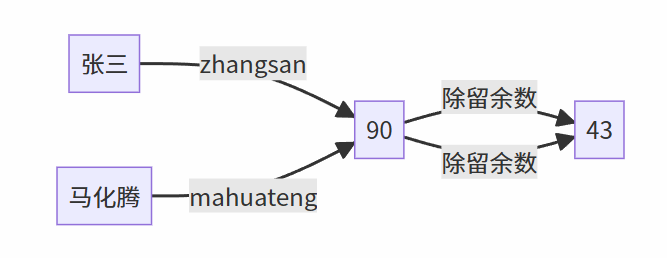
此时，马化腾跟张三虽然姓名信息毫不相干，但是计算出来的哈希地址却是冲突的。如何解决冲突？这是哈希表的第二项重要工作。

3. 解决冲突

① 开放地址法

解决冲突跟选取哈希函数一样，是可以很灵活的。最简单的想法是：既然某个哈希地址已经有别的数据了，那就换一个位置。比如将数据挪到已冲突的位置的旁边，如果旁边还是冲突那么再试试旁边，这就是所谓的开发地址法解决冲突。

这种看似简单的做法，有很多弊端：

必须保证哈希表的总大小要大于数据节点数目，否则如果数据填满了整张哈希表，那么除非扩充哈希存储数组，否则不管怎么调整位置，都不可能找到空余的地方。
多个哈希值冲突的数据节点会在冲突点附近形成"堆积"，每个形成冲突的节点都要将前面冲突所走过的路线再走一遍。
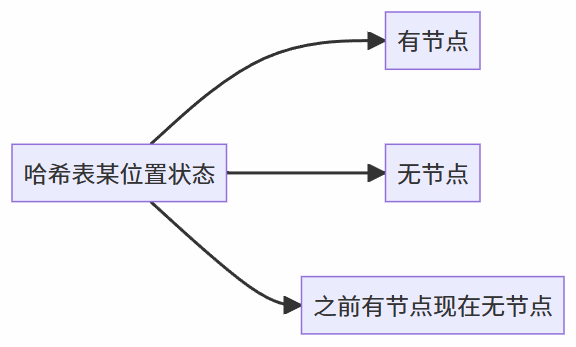
由于节点所处的真实位置与其从哈希函数计算出来的理论位置可能不一致（被冲突就不一致了），这就导致一个位置的状态不是两种，而必须是三种：有节点、无节点、之前有现在无节点。

关于上述第3个弊端，可以用如下例子加以解释：

张三入学时，根据哈希函数计算被安排到了43号桌，然后麻花藤入学时计算出来的哈希地址也是43号，于是小麻同学只能乖乖地坐在小张的旁边，44号桌。

然后，小张退学了。

然后，我们要查找小麻同学，根据哈希函数，计算出来的哈希地址是43，此时43号桌的状态如果是没人的话，那么就会误判以为班级里面没有小麻这位同学，于是产生了错误。

解决这个谬误的办法，要将这样的43号做标记为 之前有人但现在无人 的状态，这样才能顺着解决冲突的办法挨个找去，最终才能找到小麻同学。

② 链地址法（拉链法）

为了解决开放地址法的弊端，可以在冲突点处设置一条链表，让所有哈希地址冲突的节点链起来，这样就既无需担心节点数量超过哈希表大小，也无需设置节点的第三种状态。

假设有如下数据节点：

23，34，14，38，46，16，68，15，07，31，2623，34，14，38，46，16，68，15，07，31，26

假设按照如下除留余数法得到它们的哈希地址：

H(key)=key%13**

那么它们在存储进入哈希表的过程如下图所示：

三、总结

哈希表是一种为了提高查找效率的数据存储方式，其核心思想就是将节点的存储位置与节点本身对应起来（让数据与存储的地址进行关联），让我们在查找数据时无需通过比对就能直接计算得到它的位置。

要想使用哈希值来查找数据，就必须先造表，造表的过程主要解决以下两个问题：

哈希函数 -- 除留余数法
解决冲突 -- 链地址法

造表完成后，按照完全一样的哈希函数和解决冲突的办法，就可以查表，这种方式下查找的效率平均是O(1)，也就是常数级，即查找所需时间与节点个数无关。

哈希表适用场景：

节点的个数相对稳定
对查找效率极度敏感

四、哈希表实现

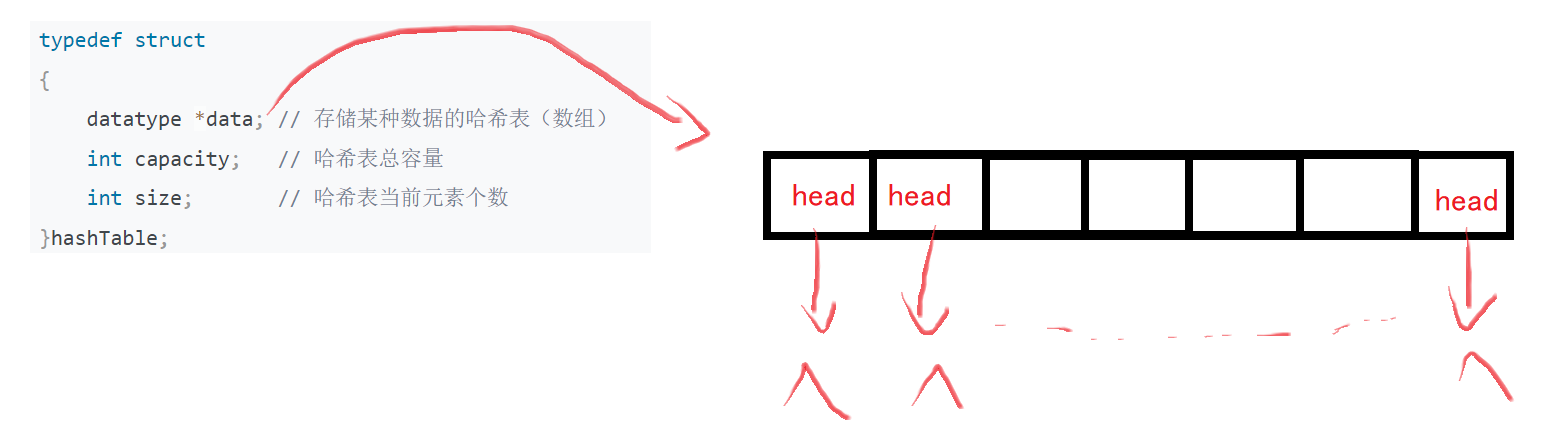
1. 设计管理结构体

typedef struct
{
    datatype *data;  // 存储某种数据的哈希表（数组）
    int capacity;    // 哈希表总容量
    int size;        // 哈希表当前元素个数
} hashTable;

2. 初始化

// 哈希表初始化函数示例
HashTable_t* HashTableInit(int capacity)
{
    HashTable_t* hashTable = (HashTable_t*)malloc(sizeof(HashTable_t));
    if (hashTable == NULL) {
        return NULL;
    }
    
    hashTable->data = (Node_t**)calloc(capacity, sizeof(Node_t*));
    if (hashTable->data == NULL) {
        free(hashTable);
        return NULL;
    }
    
    hashTable->capacity = capacity;
    hashTable->size = 0;
    return hashTable;
}

3. 添加

添加数据的流程：

根据数据的键值得到对应的哈希值
判断是否发生冲突
- 如果没有则直接存入
- 如果有则插入到冲突的链表

int Add2Hash( HashTabe_t * HashCntl , Node_t * NewNode )
{
    // 获得哈希地址
    int HashAddr = HashFunc( NewNode->Data.ID );
    printf("新节点即将加入到[%d]\n" , HashAddr) ;
    

    // 判断目标链表是否为空链表 （如果为空则标识当前数据尚未发生冲突）
    if ((HashCntl->Hash)[HashAddr] == NULL )
    {
        // 直接让头指针指向新节点
        (HashCntl->Hash)[HashAddr] = NewNode ;
        // DisplayList(  (HashCntl->Hash)[HashAddr] );
    }
    else{
        add2List(   (HashCntl->Hash)[HashAddr]  , 
                    NewNode ,  
                    (HashCntl->Hash)[HashAddr]->Next );

        // DisplayList(  (HashCntl->Hash)[HashAddr] );
    }
    
    HashCntl->Count ++ ;

    return HashCntl->Count ;
}

4.查找

查找时只需要与插入时的过程保持一致即可:

通过键值获取哈希地址
检查该地址是否有数据
- 有则尝试遍历链表寻找
- 没有则直接返回

Node_t * Find4Hash( HashTabe_t * HashCntl , int Key )
{

    // 获得哈希地址
    int HashAddr = HashFunc( Key );

    // 为了方便理解，这里把哈希表的具体元素
    //  转换为一个双向循环链表的头指针
    Node_t * head = (HashCntl->Hash)[HashAddr] ;

    if (head == NULL)
    {
        return NULL ;
    }
    else if ( head->Data.ID == Key )
    {
        return head ;
    }
    else
    {
        // 初始化让tmp指向第一个有效数据
        for (Node_t * tmp = head->Next ; tmp != head ;  tmp = tmp->Next )
        {
            printf(" 比较一次 \n");
            if (tmp->Data.ID == Key)
            {
                return tmp ;
            }
        }
    }
    
    
    return NULL ;
}

5. 删除

删除操作与链表一致，找到后剔除即可。

int RemoveFromHash(HashTable_t* HashCntl, int Key)
{
    int HashAddr = HashFunc(Key);
    Node_t* head = (HashCntl->Hash)[HashAddr];
    
    if (head == NULL) {
        return -1; // 未找到
    }
    
    // 如果是头节点
    if (head->Data.ID == Key) {
        (HashCntl->Hash)[HashAddr] = head->Next;
        free(head);
        HashCntl->Count--;
        return 0;
    }
    
    // 遍历链表查找
    Node_t* prev = head;
    Node_t* current = head->Next;
    while (current != NULL && current != head) {
        if (current->Data.ID == Key) {
            prev->Next = current->Next;
            free(current);
            HashCntl->Count--;
            return 0;
        }
        prev = current;
        current = current->Next;
    }
    
    return -1; // 未找到
}

6. 销毁

销毁则需要先把每一个链表进行销毁，然后再销毁哈希表，最后销毁管理结构体即可。

void DestroyHashTable(HashTable_t* HashCntl)
{
    if (HashCntl == NULL) {
        return;
    }
    
    // 销毁每个桶的链表
    for (int i = 0; i < HashCntl->capacity; i++) {
        Node_t* current = (HashCntl->Hash)[i];
        while (current != NULL) {
            Node_t* temp = current;
            current = current->Next;
            free(temp);
        }
    }
    
    // 释放哈希表数组
    free(HashCntl->Hash);
    // 释放管理结构体
    free(HashCntl);
}

五、哈希函数设计技巧

好的哈希函数特征
确定性：相同的键必须产生相同的哈希值

均匀性：哈希值应该均匀分布在哈希表中

高效性：计算哈希值的时间复杂度应该是O(1)

常用哈希函数

// 除留余数法
unsigned int hash_div(int key, int table_size) {
    return key % table_size;
}

// 乘法哈希
unsigned int hash_mult(int key, int table_size) {
    double A = 0.6180339887; // 黄金分割的倒数
    double product = key * A;
    return (int)(table_size * (product - (int)product));
}

// 字符串哈希 - DJB2算法
unsigned int hash_djb2(const char* str, int table_size) {
    unsigned long hash = 5381;
    int c;
    
    while ((c = *str++)) {
        hash = ((hash << 5) + hash) + c; // hash * 33 + c
    }
    
    return hash % table_size;
}

posted @ 2025-11-03 08:24 林明杰阅读(5) 评论(0) 收藏举报

刷新页面返回顶部

Jaklin

哈希表