二叉树

二叉树

一、基本概念

树是一种非线性结构，其严格的数学定义是：如果一组数据中除了第一个节点（第一个节点称为根节点，没有直接前驱节点）之外，其余任意节点有且仅有一个直接前驱，有零个或多个直接后继，这样的一组数据形成一棵树。这种特性简称为一对多的逻辑关系。

树结构示意图

常见例子

日常生活中，很多数据的组织形式本质上是一棵树。比如一个公司中的职员层级关系，一个学校中的院系层级关系，淘汰赛中的各次比赛队伍，一个家族中的族谱成员关系等，这些都是树状逻辑结构。由于树状结构表现出来都是具有层次的，因此也被称为层次结构。

树的现实例子

通常，在逻辑上表达一棵抽象的树状结构的时候，习惯于将树根放在顶部，树枝树杈向下生长，如下图所示。

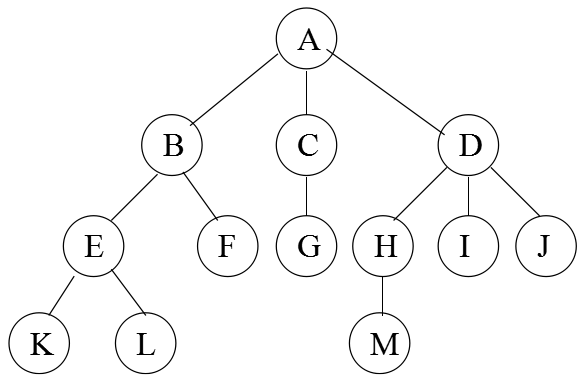
树的抽象表示

对于一棵树来说，有如下基本术语：

  • 根（root）：树的第一个节点，没有直接前驱。如上图中的A。
  • 双亲节点（parent）：某节点的直接前驱称为该节点的双亲节点，或成为父节点。例如上图中A是B的父节点。
  • 孩子节点（child）：某节点的直接后继称为该节点的孩子节点。例如上图中B、C、D均为A的孩子节点。
  • 节点的层次（level）：根节点所在的层次规定为第1层，其孩子所在的层次为第2层，后代节点以此类推。比如上图中节点E的层次是3。
  • 节点的度（degree）：一个节点拥有的孩子节点的总数，称为该节点的度。比如上图中节点B的度为2。
  • 叶子（leaf）：一棵树中度等于0的节点，被称为叶子，又称为终端节点。比如上图中K、L、F、G、M、I、J均为叶子。
  • 树的高度（height）：一棵树中所有节点的层次的最大值，称为这棵树的高度，又称为树的深度。比如上图的树的高度为4。
  • 有序树与无序树：一棵树中，如果某个节点的孩子节点之间是有次序的，则称这棵树为有序树，反之称为无序树。

二、二叉树（Binary Tree）

在各种不同的树状结构中，最常见也最重要的是二叉树（Binary Tree），下面是二叉树的定义：

  • 有序树（小中大）
  • 任意节点的度小于等于2

比如如下这棵树就是一棵二叉树。其中8是根节点，14是10的右孩子（因为二叉树是有序树，因此严格区分左右），而13则是14的左孩子。

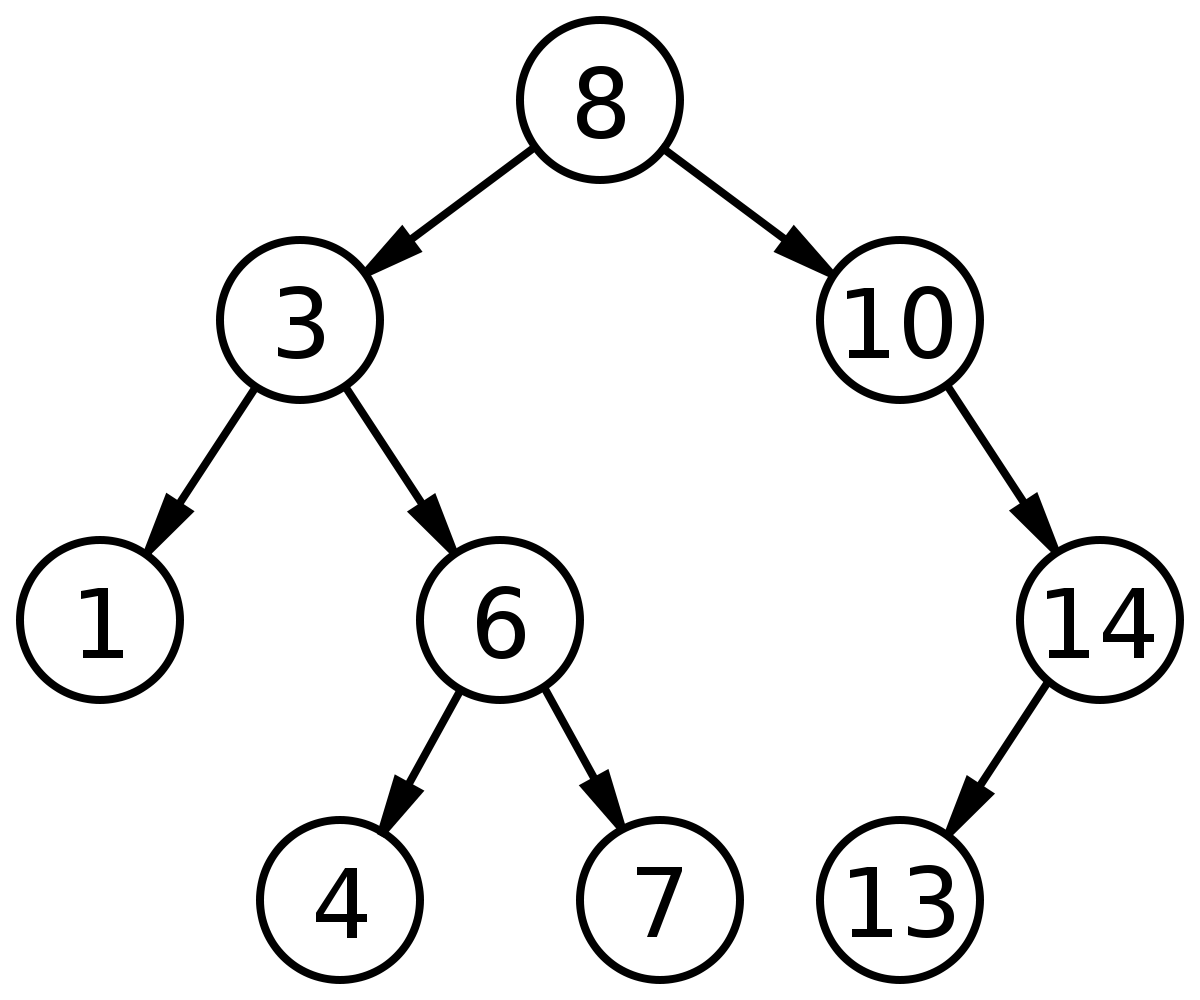
二叉树示例

为了方便对二叉树进行操作，通常会对一棵它进行标号（≈数组下标）：从上到下，从左到右进行标号：

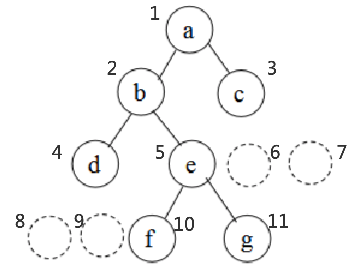
二叉树标号

注意：

没有孩子节点的地方也要标出来

二叉树特性
二叉树重要基本概念

三、存储形式

与其他逻辑结构类似，可以使用顺序存储，也可以使用链式存储。

顺序存储

由于在顺序存储，数据元素之间的逻辑关系是用物理位置来表达的，而二叉树中每一个节点都有一个对应的标号，因此可以使用标号来作为数组的下标，但除非是完美或者完全二叉树，否则会浪费存储空间，如下图所所示。

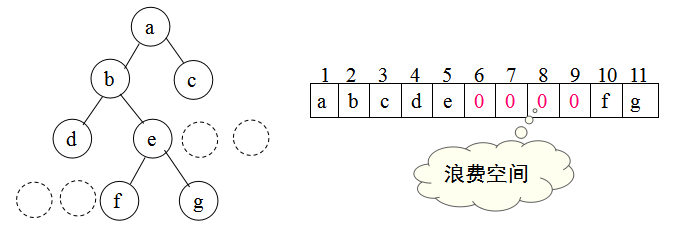
二叉树顺序存储

在顺序存储中，节点彼此之间的关系，要用到二叉树标号（≈下标）的基本特性。简单观察二叉树的标号会发现如下规律：

  • 根节点标号为1，根节点没有父节点
  • 标号为n的节点，其父节点的标号为n/2
  • 标号为n的节点，其左孩子（若有）的标号为2n，其右孩子（若有）的标号为2n+1

根据以上结论，在顺序存储的二叉树中，虽然没有任何信息连接节点e和f，但根据他们的下标序号，可以得知e是f的父节点，且f是e的左孩子。

链式存储

链式存储思路与链表类似，使用指针来直接将节点的逻辑关系串起来，比如：

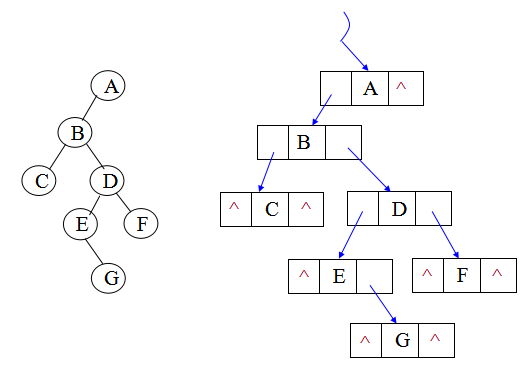
二叉树链式存储 
// 二叉树节点定义
typedef struct TreeNode {
    int data;                   // 数据域
    struct TreeNode *left;      // 左子树指针
    struct TreeNode *right;     // 右子树指针
} TreeNode, *P_TreeNode;

四、树的遍历

所谓遍历，就是按某种规律访问每一个节点。对于之前的线性表而言，遍历算法很简单，就是从头跑到尾，因为线性表是一对一的关系。但是树状结构是非线性的，因此从根节点开始遍历所有节点可以有多种不同的算法，常见的有：

  • 前序遍历：根节点 - 左子树 - 右子树
  • 中序遍历：左子树 - 根节点 - 右子树
  • 后序遍历：左子树 - 右子树 - 根节点
  • 按层遍历：从上到下，从左到右依次访问节点

其中需要注意的是，前中后序遍历，都是递归算法。以前序遍历为例，当访问完根节点，进而要访问左子树时，由于左子树本身一棵二叉树，因此也需要进行前序遍历，也是先访问左子树的根节点，然后再依次访问左子树的左子树和左子树的右子树。比如：

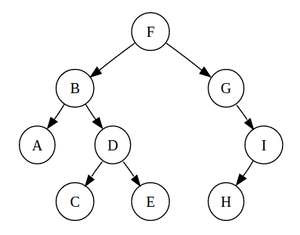
二叉树链式存储

前序遍历： F B A D C E G I H
中序遍历： A B C D E F G H I
后续遍历： A C E D B H I G F
按层遍历： F BG ADI CEH

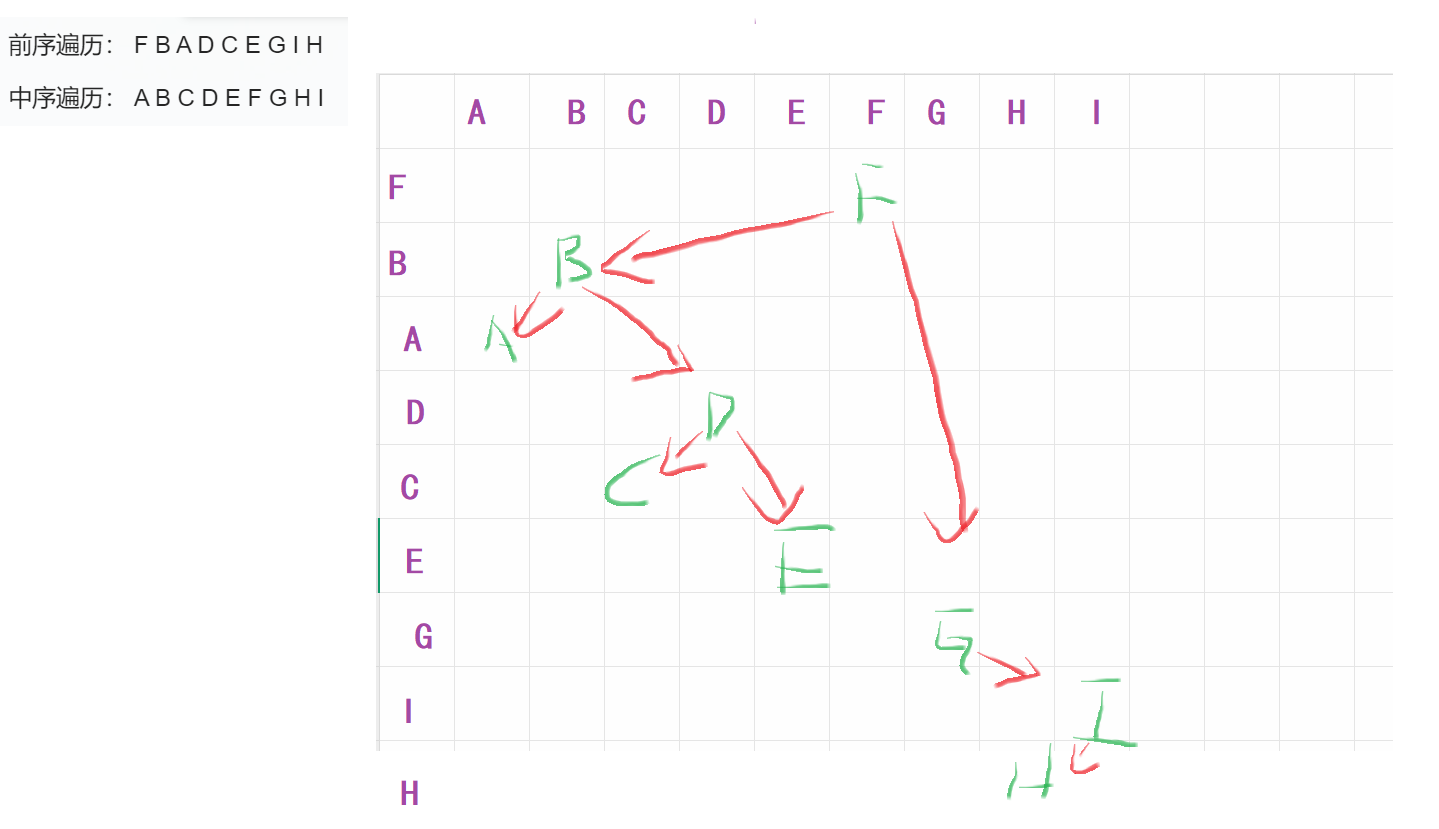
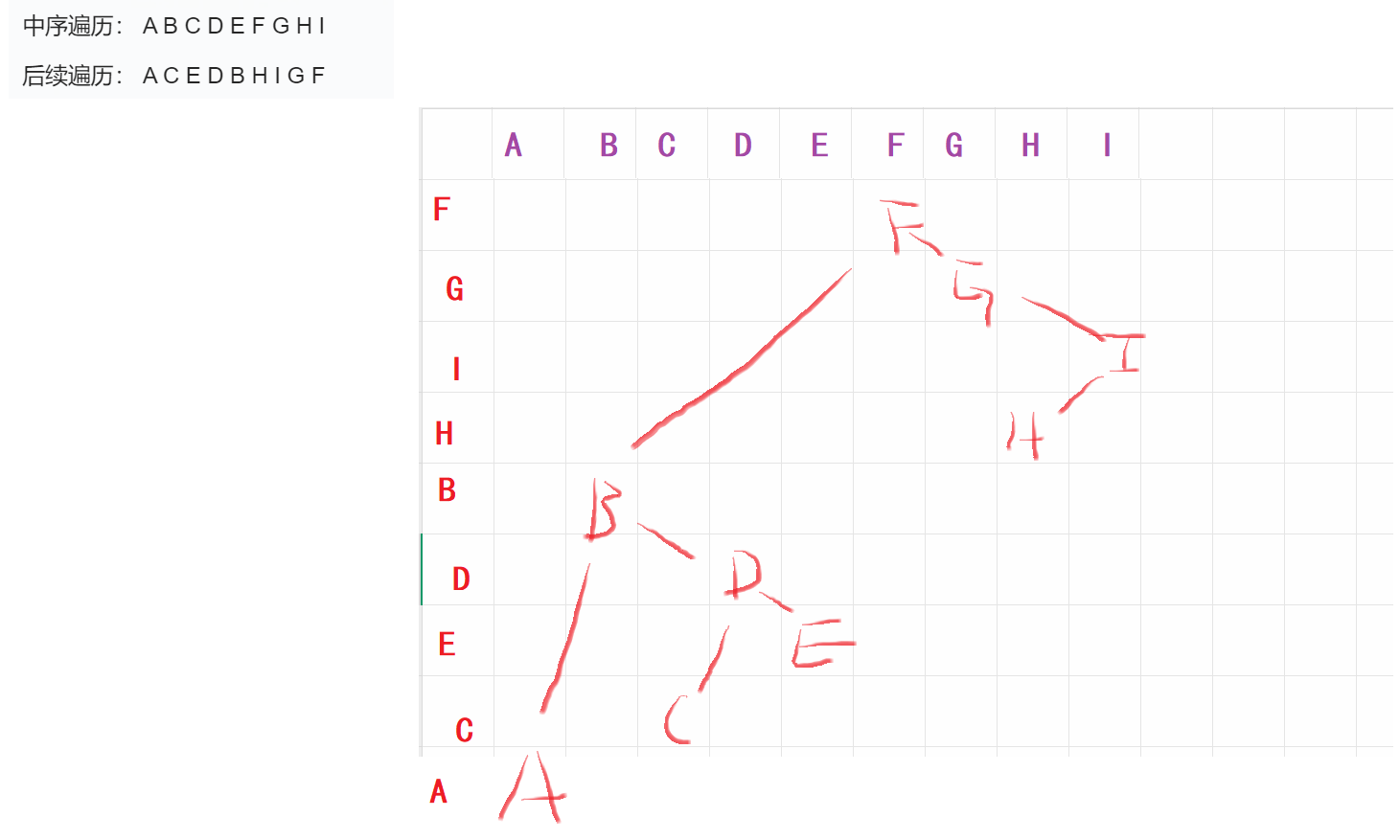
还原二叉树：
通过表格从左往右把中序填入，然后再根据前序或后续填入行的标识（前序从正向遍历并从上往下填入，后续则逆向遍历并从上往下）

二叉树链式存储
二叉树链式存储

五、二叉搜索树（BST）

1. BST的基本概念

二叉树的其中一个重要应用，是提供一种快速查找数据的方法，即：将数据节点按照某种规律形成一棵二叉树，然后利用二叉树特殊的逻辑结构减少搜索数据的次数，提高查找的效率。

这种按照某种规律构建，用来提高搜索性能的二叉树，被称为搜索二叉树（Binary Search Tree），即BST。

具体而言，二叉树提高搜索效率的秘诀在于：按照"小-中-大"（当然"大-中-小"也是一样的）的规律来存储数据，即对于任意一个节点，都可以明确找到其值大于或等于其左孩子节点，且小于或等于其右孩子节点。如下图所示：

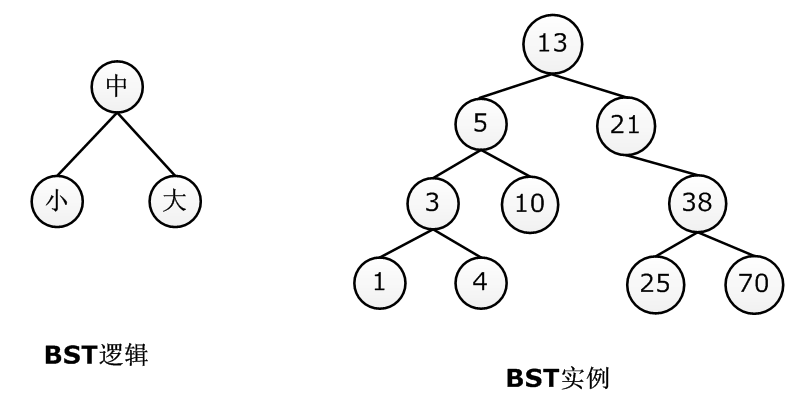
BST结构示意图

由于树中所有的节点均满足"小-中-大"的规律，因此当从根开始查找某个节点时速度比顺序查找要快得多，比如要找节点38，当发现38大于根节点13后，就可以确定13的左子树一定没有38，这就去掉了半边子树的节点。

因此，二叉搜索树又被称为二叉排序树、二叉查找树。

实际上，对于一棵二叉树而言，其搜索节点的时间复杂度，最糟糕的情形是其退化为链表，最乐观的情形是完美或完全二叉树，那么其搜索时间复杂度就是介于：

  • 最差：T(n)=O(n)
  • 最优：T(n)=O(log₂n)

2. 基础操作

① 设计数据域

typedef struct dataType {
    int key;  // 用于排序的键值
    // 其他数据成员...
} dataType_t;

② 设计节点

typedef struct TreeNode
{
    dataType_t Data ;

    struct TreeNode * L , * R ;
}BstNode_t , *P_BstNode_t;
节点示意图

③ 初始化

初始化只需要让树根指针指向NULL即可

P_BstNode_t root  = NULL ;

④ 添加节点

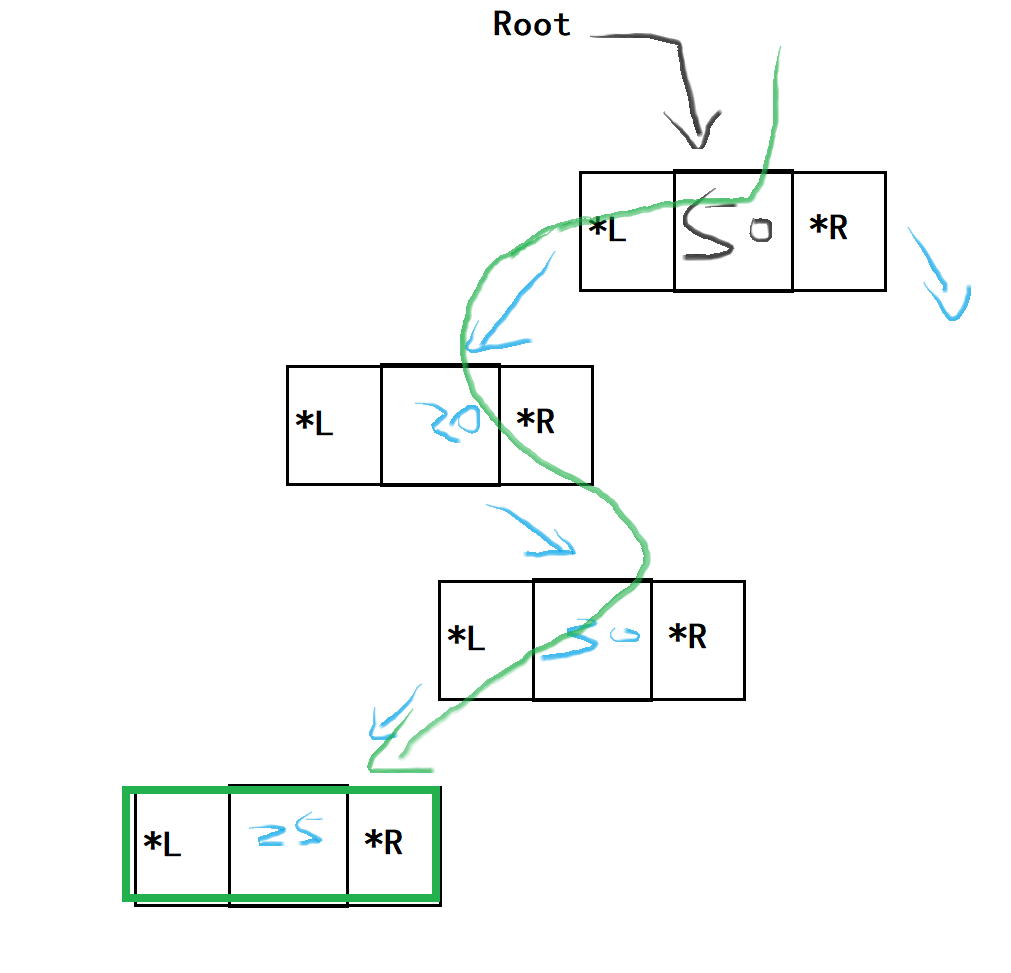
通过递归不断用root节点与新节点的数据进行比较，在比较的过程中根据大小关系决定往左或往右添加（递归），当root指向NULL 的时候直接返回新节点，让上一层的root指向该新节点。
把新节点插入后成为叶子即可。

添加节点 
P_BstNode_t Add2Tree( P_BstNode_t root , P_BstNode_t newNode )
{
    // 递归退出条件
    if (root ==  NULL)
    {
        return newNode ;
    }

    // 根据根节点的数据值与新节点的数据大小关系
    // 寻找一个合适的位置并插入到叶子位置
    if ( newNode->Data < root->Data )
    {
        /* 往左子树去 */
        root->L = Add2Tree(  root->L ,  newNode );
    }
    else {
        /* 往右子树去 */
        root->R = Add2Tree(  root->R ,  newNode );
    }
    
    return root ;
}

⑤ 遍历

a.前序、后续
参考中序遍历调整访问数据的时机即可。


b.中序
中序遍历自带升序排序魔法，当二叉树遵循小-中-大的方式排列时，中序遍历的先后顺序刚好就是小-中-大。

void InOrderTraversal( P_BstNode_t root )
{
    if (root == NULL)
    {
        return ;
    }
    
    // 往左边遍历
    InOrderTraversal( root->L );

    // 访问根节点
    printf("%d\t" , root->Data);

    // 往右边遍历
    InOrderTraversal( root->R );

}

c.按层
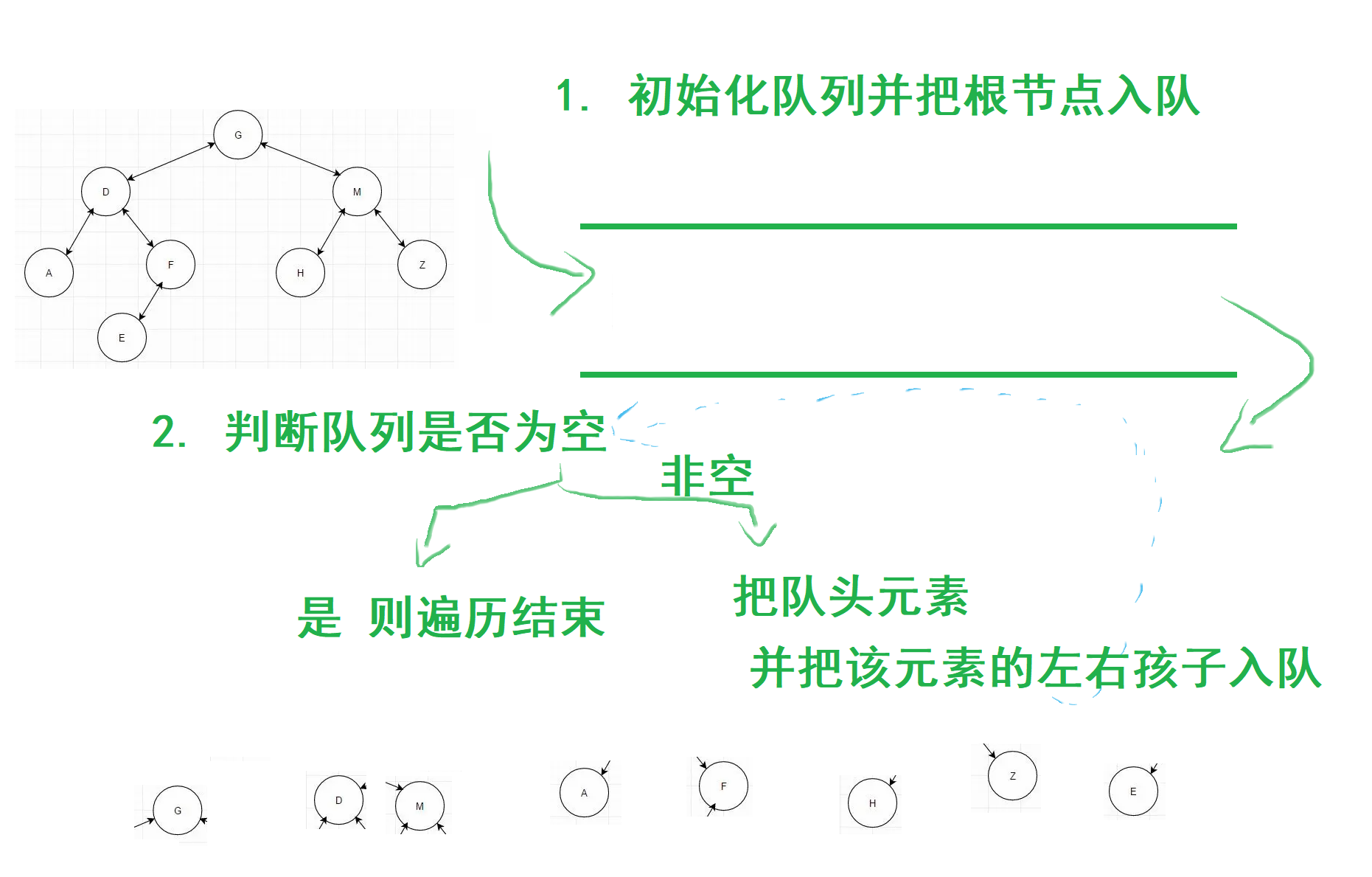
对于按层遍历，则需要借助队列来达到这一目的。具体做法是：
1.创建一个队列，并将根节点指针入队
2.判断队列是否为空：

  • a. 是则退出程序
  • b. 否则让队头元素出队，并将队头的左右孩子依次入队
  • c. 循环步骤2
按层遍历 
void TraversalByLayer( P_BstNode_t root )
{
    // 初始化队列
    Cntl_t * queue = InitQueue( );

    // 把树的根节点的指针入队
    Node_t * newNode = getNewNode ( root ) ;
    enQueue( queue  , newNode ) ;

    while(1)
    {
        // 队头元素出队
        Node_t * out = outQueue( queue ) ;
        
        // 判断队列是否为空
        if (out == NULL )
        {
            break; 
        }
        
        printf("%d\t" , out->tmp->Data) ;

        // 判断出队元素是否拥有左右孩子，如果有则依次入队
        if (out->tmp->L != NULL )
        {
            /* 如果有则把左子节点入队 */
            newNode = getNewNode ( out->tmp->L ) ;
            enQueue( queue  , newNode ) ;
        }
        if (out->tmp->R != NULL )
        {
            /* 如果有则把右子节点入队 */
            newNode = getNewNode ( out->tmp->R ) ;
            enQueue( queue  , newNode ) ;
        }
    }

    printf("按层遍历结束..\n");
    return ;
}

⑥ 删除

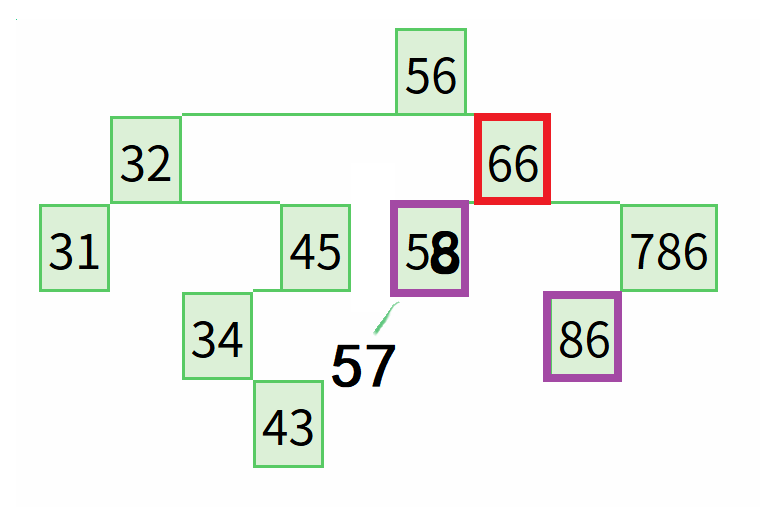
如果需要把一个数据从一棵树中剔除，那么需要考虑剔除后该树依然要保持有序。因此需要在被剔除的节点的左（左侧最接近的数据就是最右（最大）边的节点）或右（右侧最节点的数据就是最左最小）边的节点）子树中寻找最合适的数据节点用于替换，替换完之后，需要再次递归把用于替换的节点继续剔除。

删除节点 
P_BstNode_t Del4Tree( P_BstNode_t root  ,dataType_t DelData )
{
    // 递归的直接返回条件 （没找到目标节点）
    if (root == NULL)
    {
        return NULL ;
    }

    // 通过根节点的数据与目标数据进行比较决定查找的方向
    if (DelData > root->Data)
    {
        /* 往右找 */
        root->R = Del4Tree( root->R  ,  DelData );
    }
    else if (DelData < root->Data)
    {
        /* 往左找 */
        root->L = Del4Tree( root->L  ,  DelData );
    }
    else{
        /* 找到目标 */
        P_BstNode_t tmp = NULL ;
        // 检测当前找到的目标节点是否存在左子树
        // 如果存在则在他的左子树中寻找最大节点用于替换
        if (root->L != NULL)
        {
            /* 在左子树中找最大的节点的数据用于替换 */
            // 一棵树中哪个节点最大=== 最右边节点
            for (tmp = root->L ; tmp->R != NULL ; tmp = tmp->R );

            // 使用最大值来替换目标节点
            root->Data = tmp->Data ;

            // 在左子树中把用于替换的目标节点删除
            root->L = Del4Tree( root->L  , tmp->Data ) ;

        }
        // 如果不存在左子树，则尝试在右子树中寻找最小的节点用于替换
        else if (root->R != NULL )
        {
            /* 如果左边为空则在右子树中进行寻找 */
            /* 在右子树中找最小（左）的节点*/
            for (tmp = root->R  ;  tmp->L != NULL ;  tmp = tmp->L );
            
            // 使用最小值来替换目标节点
            root->Data = tmp->Data ;

            // 在右子树中把用于替换的目标节点删除
            root->R = Del4Tree( root->R  , tmp->Data ) ;
            
        }
        else{
            /* 当需要剔除的节点左右都为空时，可以直接释放 */
            free(root);
            return NULL ; // 返回NULL 
        }
    }
    
    return root ;
    
}

⑦ 销毁

使用后序遍历进行销毁二叉树

void DestroyBinaryTree( P_BstNode_t root )
{
    if (root == NULL)
    {
        return ;
    }

    DestroyBinaryTree( root->L );
    DestroyBinaryTree( root->R );

    printf("正在释放【%d】\n" , root->Data) ;
    free(root);

    return ;
}
posted @ 2025-11-01 08:10  林明杰  阅读(8)  评论(0)    收藏  举报