线性表
顺序表管理结构体 、**顺序表基本操作 **!
一、线性表概念
对于一组拥有 n 个数据元素的线性表,其严格数学定义是:其中任何一个数据元素 a[i],有且仅有一个直接前驱 a[i-1],有且仅有一个直接后继 a[i+1]。首元素 a[0] 无直接前驱,尾元素 a[n-1] 无直接后继。
满足这种数学关系的一组数据,当中的数据是一个挨着一个的,常被称为一对一关系。反之,如果数据之间的关系不是一对一的,就是非线性的。
二、顺序表
1. 基本概念
- 顺序表:顺序存储的线性表。
- 链式表:链式存储的线性表,简称链表。
顺序存储就是将数据存储到一片连续的内存中,在C语言环境下,可以是具名的栈数组(int arr[10] ),或者是匿名的堆数组( calloc( 10 , sizeof(int) ) )。
存储方式不仅仅只是提供数据的存储空间,而是必须要能体现数据之间的逻辑关系。当采用顺序存储的方式来存放数据时,唯一能用来表达数据间本身的逻辑关系的就是存储位置。比如队列中的两个人,小明和小花,如果小明在逻辑上排在相邻的小花的前面,那么在存储位置上也必须把小明存放在相邻的小花的前面。
2. 基本操作
顺序表设计一般而言,为了方便操作顺序表,需要一个专门管理顺序表的”管理结构体“,管理结构体中一般会包含:
a.顺序表总容量,方便判断顺序表是否已满。
b.顺序表当前最末元素下标位置
c.顺序表指针
① 数据类型设计
// 设计数据类型
typedef struct DataType
{
int Num ;
char Name[32];
}DataType_t , *P_DataType_t;
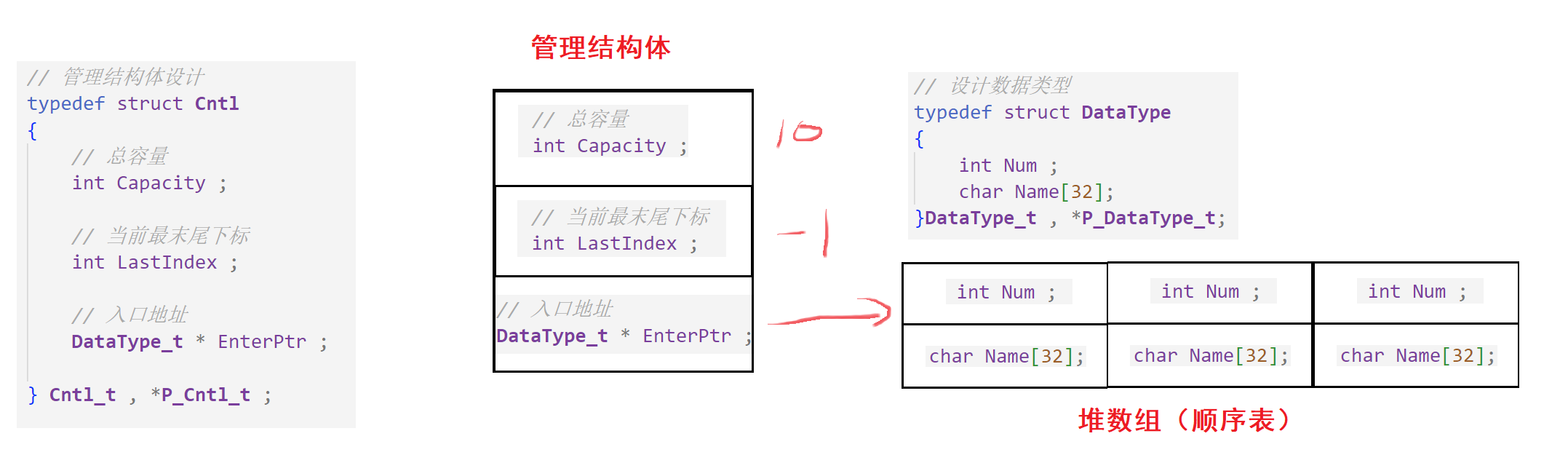
② 管理结构体的设计
// 管理结构体设计
typedef struct Cntl
{
// 总容量
int Capacity ;
// 当前最末尾下标
int LastIndex ;
// 入口地址
DataType_t * EnterPtr ;
} Cntl_t , *P_Cntl_t ;
③ 初始化顺序表
Cntl_t * InitList( unsigned int Capacity )
{
// 申请管理结构体的内存空间
Cntl_t * cntl = calloc( 1 , sizeof(Cntl_t) );
if (cntl == NULL)
{
perror("calloc cntl error") ;
return NULL ;
}
// 管理结构体初始化
cntl->Capacity = Capacity ;
cntl->LastIndex = -1 ;
// 申请存储数据的堆内存
cntl->EnterPtr = calloc( Capacity , sizeof( DataType_t ) );
if (cntl->EnterPtr == NULL)
{
perror("calloc Data Arr error") ;
return NULL ;
}
// 返回管理结构体
return cntl ;
}
④ 有序添加数据
有序插入数据,当前示例默认按照数据的编号进行升序排序:
- 判断当前顺序表是否已满
- 从左往右依次比较并寻找第一个比新数据大的节点
- 找到位置后把当前位置数据及其右边的数据进行移动
- 为了避免数据被覆盖一般选择自右向左依次右移
- 移动结束后空出来一个位置用于存储新数据,因此直接存入即可
- 更新末尾下标并返回当前有效数量
void RightShift( DataType_t * Enter , int EndIndex , int StatrIndex )
{
for (int i = StatrIndex ; i >= EndIndex ; i-- )
{
Enter[i+1] = Enter[i] ;
}
return ;
}
int OrderlyAdd2List( Cntl_t * cntl , DataType_t * NewData )
{
// 判断是否已满
if ( cntl->LastIndex >= cntl->Capacity )
{
printf("当前顺序表已满..\n") ;
return -1 ;
}
// 寻找合适位置
int i ;
for ( i = 0; i <= cntl->LastIndex ; i++)
{
// 寻找第一个比新数据大的原始数据
if ( NewData->Num < (cntl->EnterPtr+i)->Num )
{
/* 挪出位置 */
RightShift( cntl->EnterPtr , i , cntl->LastIndex );
break;
}
}
// 进行插入
cntl->EnterPtr[i] = *NewData ;
// 更新末尾下标
cntl->LastIndex ++ ;
// 返回当前顺序表的有效数据数量
return cntl->LastIndex + 1 ;
}
⑤ 遍历显示
void DisplayList( Cntl_t * cntl )
{
if (cntl->LastIndex < 0)
{
printf("顺序表为空..\n");
return ;
}
for (int i = 0; i <= cntl->LastIndex ; i++)
{
printf("%d \t %s\n" ,
(cntl->EnterPtr+i)->Num ,
(cntl->EnterPtr+i)->Name);
}
printf("\n");
return ;
}
⑥ 查找数据(二分法查找)
顺序表最大的优势就是可以使用偏移量实现立即访问,如果数据本身按照某种次序排序,则可以使用二分查找法实现快速搜索。
int DichotomyFind( Cntl_t * cntl , int Num ,
int LeftIndex , int RightIndex )
{
int retIndex = -1 ;
// 退出条件
if (cntl->EnterPtr == NULL || cntl->LastIndex < 0 ||
LeftIndex > RightIndex )
{
printf("直接退出..\n");
return -1 ; // -1 表示查找不到
}
// 计算得到中间原始的下标
int Mid = LeftIndex + (RightIndex - LeftIndex)/2 ;
// 比较并确定寻找的方向
if ( Num < (cntl->EnterPtr+Mid)->Num )
{
/* 往左边找 */
retIndex = DichotomyFind( cntl , Num , LeftIndex , Mid-1 );
}
else if ( Num > (cntl->EnterPtr+Mid)->Num)
{
/* 往右边找 */
retIndex = DichotomyFind( cntl , Num , Mid + 1 , RightIndex );
}
else{
/* 找到了 */
return Mid ;
}
// 返回结果
return retIndex ;
}
⑦ 删除数据
删除操作可以在前方的查找功能之后实现,找到目标数据,然后把他从顺序表中抹除即可。
DataType_t * Del2List( Cntl_t * cntl , int DelIndex )
{
DataType_t * tmp = calloc(1, sizeof(DataType_t)) ;
if ( cntl->EnterPtr == NULL || cntl->LastIndex < 0 || DelIndex < 0 )
{
printf("参数异常..\n");
free(tmp);
return NULL ;
}
// 临时存储被剔除的目标数据
*tmp = cntl->EnterPtr[DelIndex];
// 左移覆盖
LeftShift( cntl , DelIndex );
// 更新当前有效数据量
cntl->LastIndex -- ;
return tmp ;
}
⑧ 修改数据
修改数据实际上可以借助查找+删除+有序插入来实现修改,并可以保持数据被修改后依然有序。
void ModifyData( Cntl_t * cntl , int Num )
{
// 找到目标数据
int findIndex = DichotomyFind(
cntl , Num , 0 , cntl->LastIndex );
if (findIndex < 0 )
{
printf("找不到目标数据..\n");
return ;
}
printf("找到目标数据:%d - %s \n" ,
cntl->EnterPtr[findIndex].Num,
cntl->EnterPtr[findIndex].Name );
// 获得新数据
printf("请输入新的数据:\n");
DataType_t NewData = GetNewData();
// 剔除原有数据
DataType_t * tmp = Del2List(cntl , findIndex );
free(tmp);
// 重新插入
OrderlyAdd2List(cntl , &NewData);
}
⑨ 销毁
销毁实际上是需要把程序中用到所有堆内存进行释放,避免出现内存泄漏
经过分析当前程序中只有两块内存未释放(管理结构体 + 堆数组);
void DestructionList( Cntl_t * cntl )
{
free(cntl->EnterPtr);
free(cntl);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号