[笔记] 高数笔记

函数极限

设函数 \(f(x)\) 在点 \(x_0\) 的某一去心邻域内有定义，如果存在常数 \(A\) ，对于任意给定的正数 \(\varepsilon\)（无论它多么小），总存在正数 \(\delta\)，使得对于 \(0<|x-x_0|<\delta\)，均有 \(f(x)-A<\varepsilon\)，那么常数 \(A\) 就叫做函数 \(f(x)\) 当时 \(x\rightarrow x_0\) 的极限，记作

\[\lim\limits_{x\rightarrow x_0} f(x)=A \]

夹逼定理：求函数的极限时，我们可以通过上界和下界两个函数去夹某个函数 \(f(x)\) ；如

\[\sin(x)<x<\tan(x)\\ \Rightarrow \frac{\sin(x)}{x}<\frac{\sin(x)}{\sin(x)}=1,\frac{\sin(x)}{x}>\frac{\sin(x)}{\tan(x)} =\cos(x)\\ \Rightarrow \lim\limits_{x\to 0} \frac{\sin(x)}{x}=1 \]

导数与斜率

斜率：对于一次函数 \(y=kx+b\) ，\(k\) 即为斜率；

导数：\(f’(x)=\lim\limits_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\) ，也可记做 \(\frac{{\rm d} x}{{\rm d} y}\)

导数存在性：从左侧与右侧逼近极限相同时才可以定义导数 \(\lim\limits_{\Delta x\to 0^+}\frac{f(x+\Delta x)-f(x)}{\Delta x} = \lim\limits_{\Delta x\to 0^-}\frac{f(x+\Delta x)-f(x)}{\Delta x}\)

导数表：

导数运算法则：

\[(u \pm v)' = u' \pm v'\\ (uv)'= u'v + v'u\\ (\frac uv)'=\frac{(u'v-v'u)}{v^2}\\ (c \cdot f(x))'=c \cdot f'(x) \\ (f(g(x)))'=f'(g(x)) \cdot g'(x) \]

高阶导数：一阶导函数的导数称为二阶导数，二阶以上的导数可由归纳法逐阶定义。二阶和二阶以上的导数统称为高阶导数。从概念上讲，高阶导数可由一阶导数的运算规则逐阶计算。

\(f''(x_0)=\lim \limits_{\Delta x\to 0} \frac{f'(x+x_0)-f'(x_0)}{\Delta x}=\lim \limits_{\Delta x\to 0} \frac{f(x_0+2\Delta x)-2f(x_0+\Delta x)+f(x_0)}{\Delta x ^2}\)，记做 \(\frac{\mathrm{d}^2 y }{\mathrm{d}x^2}\) 。

一阶导描述函数增减性，函数极值点一阶导为 \(0\) ；二阶导描述函数的凹凸性。

自然对数\(e\)：

\(e=\lim\limits_{n \to \infty}(1+\frac{1}{n})^n=2.718281828459\cdots\)

\((e^x)'=e^x,(\ln(x))'=\frac{1}{x}\)

洛必达法则：

若 \(f(x)\) 和 \(g(x)\) 在 \(a\) 点处为 \(0\) ，即 \(0/0\) 类型

\(\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a} \frac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}}=\lim\limits_{x\to a}\frac{f'(x)}{g'(x)}\)

牛顿迭代法：

求解 \(f(x)=0\) ：随机一个初始点，对于当前点求导，计算与 \(x\) 轴交点作为下一次的 \(x_{next}\) ，即

\[x_{next}=x-\frac{f(x)}{f'(x)} \]

当 \(x<eps\) 终止。

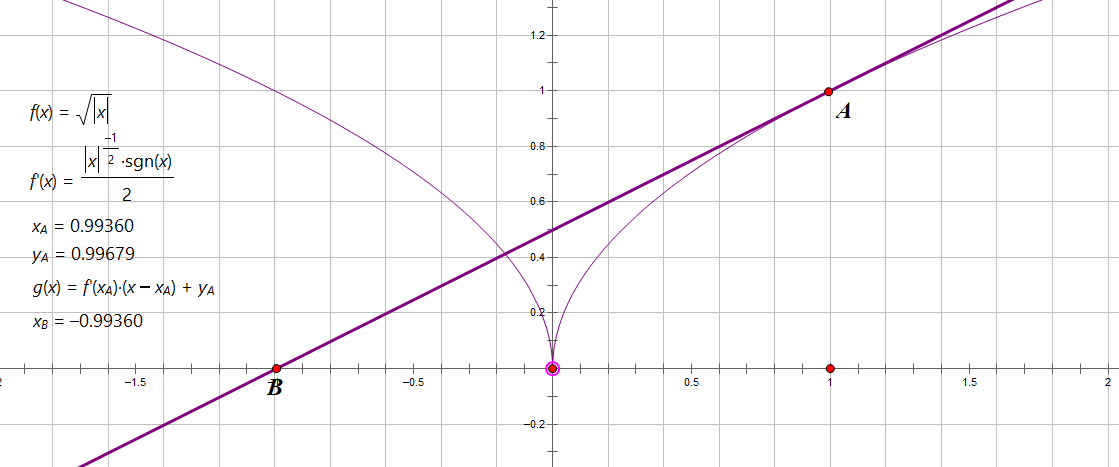
对于大部分函数有效；有些函数会失效，如 \(f(x)=\frac{1}{x}\) (没有 \(0\) 点)；\(f(x)=\sqrt{|x|}\) （来回横跳）

积分

定积分

\(S=\int_{a}^b f(x)\mathrm{d}x\)

黎曼积分，黎曼和： \(S=\lim\limits_{n\to \infty} \sum\limits_{k=1}^n f(k)\times (x_k-x_{k-1})\)
这样我们可以方便的求定积分。

\[\begin{aligned} \int_0^cx^2\mathrm{d}x &=\lim\limits_{n\to \infty} \sum\limits_{k=1}^n (k\frac{c}{n})^2 \cdot \frac{c}{n}\\ &=\lim\limits_{n\to \infty} (\frac{c}{n})^3 \sum\limits_{k=1} k^2\\ &=\frac{c^3\cdot n\cdot (n+1) \cdot (2n+1)}{n^3\cdot 6}\\ &=\frac{c^3(2n^3-3n^3+n)}{6n^3}\\ &=\frac{c^3}{3}\\ \int_0^c x^n\mathrm{d}x &=\frac{c^{n+1}}{n+1} \end{aligned} \]

积分与微分的关系：

\[\begin{aligned}\\ \int_a^b f'(x)\mathrm{d}x &= \lim\limits_{n \to \infty}\sum\limits_{0\leq k<n}f'(x_k)\mathrm{d}x\\ &=\lim\limits_{n \to \infty}\sum\limits_{0\leq k<n}\frac{f(x_{k+1})-f(x_k)}{x_{k+1}-x_k}(x_{k+1}-x_k)\\ &=\lim\limits_{n \to \infty}\sum\limits_{0\leq k<n} f(x_{k+1})-f(x_k)\\ &=\lim\limits_{n \to \infty}f(x_{n-1})-f(x_0)\\ &=f(b)-f(a)\\ &=f(x)|_a^b \end{aligned}\\ \]

即牛顿-莱布尼茨公式。

自适应辛普森积分法

详见

inline double f(double x) {}
inline double simpson(double l,double r) 
	{return (f(l)+4*f((l+r)/2)+f(r))*(r-l)/6;}
inline double integral(double l,double r,double ans) {
	register double md=(l+r)/2;
	register double LL=simpson(l,md),RR=simpson(md,r);
	if(fabs(LL+RR-ans)<=15*eps) return LL+RR-(LL+RR-ans)/15;
	return integral(l,md,LL)+integral(md,r,RR);
}

integral(l,r,simpson(l,r));

不定积分

\[\int f(x)\mathrm{d}x=g(x)+c \]

积分表：

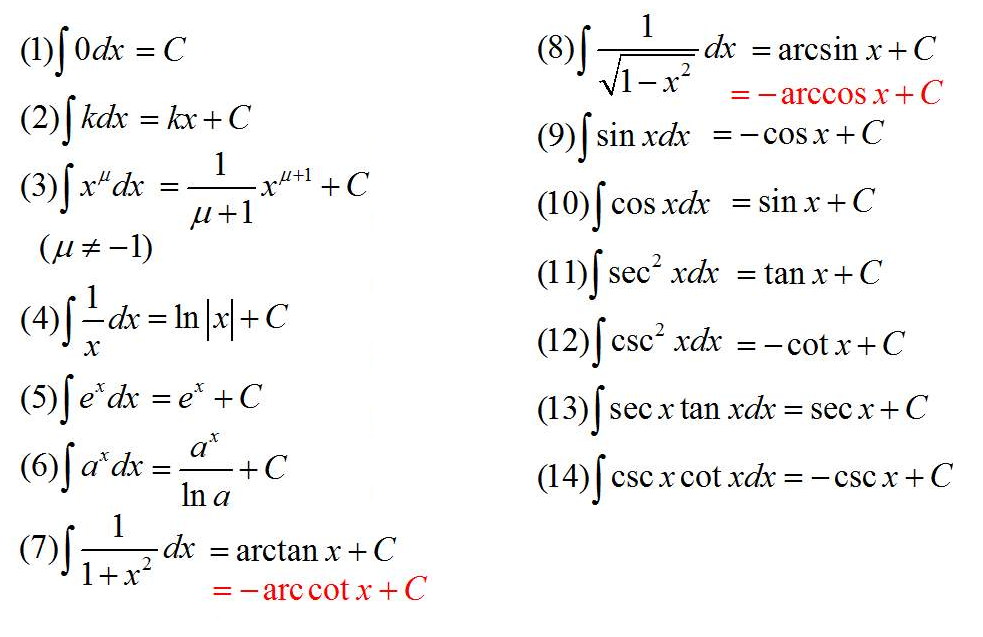
积分与无穷向量

对于一个函数 \(f(x)\) 可以理解为一个无穷维的向量，每个点的函数值是一个维度，那么两个函数 \(f(x)\) 和 \(g(x)\) 的内积就可以理解为 \(\int f(x)g(x)\mathrm {d}x\)

函数正交基：

对于线性空间的一组正交基，需要满足对于任意两个基向量 \(A,B\) 有 \(A\cdot B=0\)

空间中一个点 \(x\) 在正交基 \({A}\) 上的坐标为 \(\frac{A\cdot x}{A\cdot A}\)

施密特正交化：

大致就是如果两个向量 \(A\cdot B\ !=0\) ，我们可以让 \(B'=B-\frac{|B|\cos<A,B>}{|A|}A\) 得到与 \(A\) 正交的向量 \(B'\) 。

函数最优化

给定一多元函数 \(f(x)→R\)，\(x\) 为多个参数组成的向量，求 \(f(x)\) 最小值以及寻找使得函数值最小的向量 \(x^{*}\)

迭代法（就是爬山算法）：初始随机一个点 \(a\)，随机一方向 \(d\) ，找一 \(\lambda\) 使 \(f(x+\lambda d)\) 变小，不断重复。

若 \(f(x)\) 存在导数，则有更好的方法：

偏导：对于二元函数 \(f(x,y)\) ，在 \((x0,y0)\) 处固定 \(y\) 不变移动 \(x\) ，可以得到一个单变量函数 \(g(x)\) ，同理固定 \(x\) 不变可以得到 \(h(y)\)；此时可以定义某一个方向的导数 \(\frac{\partial f}{\partial x}\) ，\(\frac{\partial f}{\partial y}\)

梯度：\(\nabla f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\)

那么 \(f(x+\Delta x,y+\Delta y)\approx f(x,y)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y,|(\Delta x,\Delta y)|\to 0且为定值\) 。注意到后面的部分实际是一个点积，此时显然 \((\Delta x,\Delta y)\) 与 \((\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\) 共线时 \(f(x+\Delta x,y+\Delta y)\) 有最大值。

函数极值条件：函数取极值时一定要求切线水平（导数为 \(0\) ）；多元函数体现为各个方向偏导数均为 \(0\) （必要不充分条件，比如鞍点：\(y=x^3,z=x^2-y^2\) ）。

无约束函数极值

我们可以直接带入偏导数为 \(0\) 的极值条件解方程。

例:

求 \(f(x)=(x_1-x_2-2)^2+(x_2-1)^2\) 的最小值。

\(\nabla f(x)=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2})=(2(x_1-x_2-2),-2(x_1-x_2-2)+2(x_2-1))=(0,0)\)

拉格朗日乘数法

设给定多元函数 \(f(x)\) 和附加条件 \(\varphi (x)=0\) ，\(x\) 为向量，为寻找 \(z=f(x)\) 在附加条件下的极值点，**构造拉格朗日函数 \(L(x,\lambda)=f(x)+\lambda\varphi(x)\) **，为关于 \(x\) 向量与 \(\lambda\) 向量的二元函数。

此时有 \(\min\limits_{x} f(x)=\min\limits_{x}\{ \max\limits_{\lambda}(L(x,\lambda)\}=\min\limits_{x}\{\max\limits_{\lambda}(f(x)+\lambda\varphi(x))\}\)

理解：首先我们要符合 \(\varphi(x)=0\) ，否则当 \(\lambda\to \infty\) 是 \(\min\limits_{x}\{ \max\limits_{\lambda}(L(x,\lambda)\} \to \infty\) ，一定不是最终答案；然后在符合条件的函数中取个最值。

求解： \(f(x)\) 为最优的必要条件是拉格朗日函数 \(L\) 梯度为 \(0\) ：\(\left\{ \begin{matrix} \nabla_x L(x,\lambda)=0\\ \nabla_\lambda L(x,\lambda)=0\\ \end{matrix} \right.\)

例：

求 \((x,y,z)\) 使得 \((x-4)^2+y^2+z^2\) 最小，并且 \(x+y+z=3, 2x+y+z=4\)

多项式逼近

泰勒展开

\(f(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + a_3(x - x_0)^3 + ...\)

通常只关心 \(x_0=0\) 处的取值，得到麦克劳林公式：\(f(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots=\sum\limits_k a_k x^k\)

结论：对于大部分常见的好函数，这种展开都是存在的，而且是唯一的，并且对于全体实数全部成立的。

计算方法：\(f^{(n)}=\sum\limits_{k\geq n} \frac{k!}{(k-n)!}a_k x^{k-n},a_n=\frac{f^{(n)}(0)}{n!}\)

常见泰勒级数：

\[\begin{aligned}\\e^x&=\sum\limits_{n=0}^\infty \frac{x^n}{n!} &x\in(-\infty,+\infty)\\\ln(x+1)&=\sum\limits_{n=0}^\infty \frac{(-1)^n}{n+1} x^{n+1} &x\in(-1,1]\\\sin(x)&=\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1} &x\in (-\infty,+\infty)\\\cos(x)&=\sum\limits_{n=0}^\infty\frac{(-1)^n}{2n!}x^{2n} &x\in (-\infty,+\infty)\\\frac{1}{1-x}&=\sum\limits_{n=0}^\infty x^n &|x|<1\\\frac{1}{1+x}&=\sum\limits_{n=0}^\infty (-1)^nx^n &|x|<1\\\end{aligned}\\ \]

欧拉公式

\(e^{i\theta}=\cos(\theta)+i\sin(\theta)\) （可以由上面的展开式看出）

特别地 \(e^{i\pi}=-1\)

---

2020.01.24