[笔记] 2-SAT

一定要加逆否命题啊

POJ3678

基本逻辑。
p||q=1 p为0，q必为1 !p->q !q->p
p||q=0 p为0，q必为0 p->!p q->!q
p&&q=1 p为1，q必为1 !p->p !q->q
p&&q=0 p为1，q必为0 p->!q q->!p
p^ q=1 p为0，q必为1 
  		 p为1，q必为0
p^ q=0 p为0，q必为0 !p->!q(原命题) q->p(逆否命题)
  		 p为1，q必为1 p->q(原命题) !q->!p(逆否命题)

POJ3207

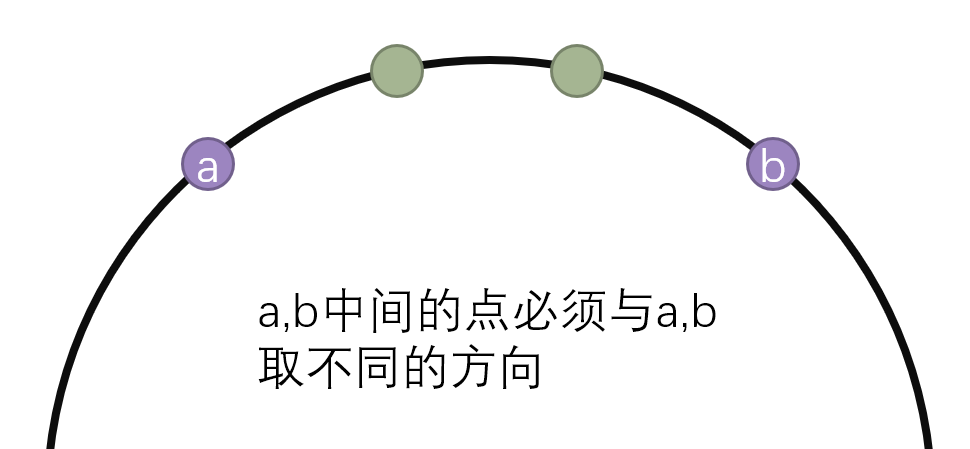
平面上，一个圆，圆的边上按顺时针放着n个点。现在要连m条边，
比如a，b，那么a到b可以从圆的内部连接，也可以从圆的外部连接。
给你的信息中，每个点最多只会连接的一条边。问能不能连接这m条边，
使这些边都不相交。

Luogu P3825 [NOI2017]游戏

先把 \(a\) 赛道转化为 选 \(b\) 否则选 \(c\) ，然后就可以 \(2-SAT\) 辣。

枚举每个不确定的赛道，注意我们只用枚举两种即可，因为两种类型的赛道即可包含选所有车的情况。

\(\mathcal{O}(2^d(n+m))\)

#include<iostream>
#include<cstdio>
#include<cstring>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
  register char s; while(!isdigit(s=getchar())) f=s=='-'?-1:f;
  do x=x*10+(s^48); while(isdigit(s=getchar())); return x*f;
} const int M=400010,N=200010;
int n,d,m;
char s[N],ans[N]; int pos[N];
int vr[M],nxt[M],fir[N],c[N],dfn[N],low[N],stk[N],cnt,num,top,C;
bool ins[N];
inline void add(int u,int v) 
  {vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
struct node {int u,v,a,b;}e[N];
inline void tarjan(int u) {
  dfn[u]=low[u]=++num;
  stk[++top]=u,ins[u]=true;
  for(R i=fir[u];i;i=nxt[i]) { 
    R v=vr[i]; 
    if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
    else if(ins[v]) low[u]=min(low[u],dfn[v]);
  } if(dfn[u]==low[u]) {
    R v; ++C;
    do v=stk[top--],c[v]=C,ins[v]=false; while(u!=v);
  }
}
inline bool ck() {
  for(R i=1;i<=2*n;++i) if(!dfn[i]) tarjan(i);
  for(R i=1;i<=n;++i) {
    if(c[i]==c[i+n]) return false;
    if(c[i]<c[i+n]) ans[i]=(s[i]=='A')?'B':'A';
    else ans[i]=(s[i]=='C')?'B':'C';
  }
  for(R i=1;i<=n;++i) putchar(ans[i]);
  return true;
}
inline void main() {
  n=g(),d=g();
  scanf("%s",s+1);
  for(R i=1,t=0;i<=n;++i) {
    s[i]-=32;
    if(s[i]=='X') pos[t++]=i;
  } m=g();
  for(R i=1;i<=m;++i) 
    e[i].u=g(),e[i].a=getchar(),
    e[i].v=g(),e[i].b=getchar();
  for(R S=0,lim=1<<d,t1,t2;S<=lim;++S) {
    memset(fir,0,sizeof fir),cnt=C=top=0;
    memset(dfn,0,sizeof dfn),
    memset(low,0,sizeof low),
    memset(ins,0,sizeof ins),
    memset(low,0,sizeof low);
    for(R i=0;i<d;++i) s[pos[i]]=(S>>i&1)?'A':'B';
    for(R i=1;i<=m;++i) {
      if(e[i].a==s[e[i].u]) continue;
      if(e[i].b==s[e[i].v]) {
        if(e[i].a=='C'||(e[i].a=='B'&&s[e[i].u]=='C')) 
          add(e[i].u+n,e[i].u); //选第二组的
        else add(e[i].u,e[i].u+n);
        continue;
      }
      t1=(e[i].a=='C'||(e[i].a=='B'&&s[e[i].u]=='C'))*n;
      t2=(e[i].b=='C'||(e[i].b=='B'&&s[e[i].v]=='C'))*n;
      add(e[i].u+t1,e[i].v+t2);
      add(e[i].v-t2+n,e[i].u-t1+n);
    } if(ck()) return ;
  } printf("-1"); 
}
} signed main() {Luitaryi::main(); return 0;}

---

2020.01.17