一句话题解（10月，11月上旬）

还是补一些代码吧。

P3594 [POI2015]WIL-Wilcze doły：答案的右端点增加，左端点不降，于是滑动窗口维护区间长为 \(d\) 的最大值。

UVA1364 Knights of the Round Table：建补图，搞点双，易知题意是求多少个点不被奇环包含；因为想一想所有图论知识（雾），好像只有点双的逻辑是对的，所以点双他！

P3534 [POI2012]STU-Well：二分答案，先修改原序列到合法（正着扫一遍+反着扫一遍），然后枚举每一个位置计算答案。

AT2164 Rabbit Exercise：先拆式子，然后发现一次转移就是\(\frac{1}{2}((2*a_{i-1}-a_i)+(2*a_{i+1}-a_i))=a_{i-1}+a_{i+1}-a_i\),即原序列变为\(a_{i-1},a_{i-1}+a_{i+1}-a_i,a_{i+1}\)。众所周知（雾），见到一次的式子可以想一想前缀和 or 差分，于是我们差分一波发现，\(a_{i-1},a_i-a_{i-1},a_{i+1}-a_i\)与后来序列的差分\(a_{i-1},a_{i+1}-a_i,a_i-a_{i-1}\) 只是交换了一项，所以我们可以将一次蹦跳转换成交换；根据期望的线性性，我们可以叠加每个一次操作；这样便可以看作是一种轮 换；显然我们可以去找这些环（轮换）的 \(sz\)，即循环节。而我们把操作次数对循环节取模就ok了。

P3533 [POI2012]RAN-Rendezvous：由于是内向森林，所以我们只能向环上跳。所以分为三种情况：两点不在同一棵基环树里，即不连通；两点在同一棵基环树，但不在同一棵子树里，那最后的汇集点一定是两个点对应子树的根，即对应环上的两点其中之一；两点在同一棵基环树并且在同一棵子树里，那就是两点的lca。

P2047 [NOI2007]社交网络：floyed求出最短路长度 \(d[i][j]\) 和数目 \(s[i][j]\) ；然后我们枚举每个点，若 \(d[i][j]==d[i][k]+d[k][j]\)，那经过他的最短路条数即为 \(s[i][k]*s[k][j]\) ；

P1841 [JSOI2007]重要的城市：考虑如何判断一个点是最短路必经点：他指向的点入度为1。

P2860 [USACO06JAN]冗余路径Redundant Paths：题意要求任意两点有两条不交边的路径，即是要把原图改成边双（没有割边）。于是我们可以先缩点，然后变成了一棵树，思索如何把树变成点双，我们可以连接两条不在同一棵子树（对于根节点来说）的叶子来构成一个环（为了使到根节点的所有边都进环）。

P3199 [HNOI2009]最小圈：01分数规划，找负环，dfs spfa。

P4819 [中山市选]杀人游戏：其实就是求最少问几个人就可以知道凶手。显然先要缩点，我们对于一个环中的， 只要查一个就可以知道所有人；而缩完点后，只有没有入度的点才会询问。
但是我们还要考虑一种特殊情况，就是我们可以利用排除法，少询问一个孤立点（并且要求不询问这个点不影响后继节点，即孤立点的所有出点的入度\(\geq\) 2）。

P4040 [AHOI2014/JSOI2014]宅男计划：好题，贪心；通过lky提示（雾）意识到我们可以三分天数，因为不可能你每一天都订餐（每天都给快递小哥钱），也不可能一次定好餐，因为保质期越长越贵。

P3119 [USACO15JAN]草鉴定Grass Cownoisseur：首先缩点，要求是改一条边的方向，使缩完点后的DAG中出现一个环。我们可以跑出每连通块 \(u\) 到 \(1\) 所在连通块的最长路 \(d[u]\)，并建反图跑出每个联通块 \(u\) 到 \(1\) 的最长路 \(h[u]\)，这样我们可以枚举每一条边 \((u,v,w)\) 并把它反过来，求出 \(d[v]+w[i]+h[u]\) 中的 max 即可。

P3546 [POI2012]PRE-Prefixuffix 神奇的递推+哈希

P3396 哈希冲突：值域分块，标准根号算法。

P2296 寻找道路：海星，先倒着跑一遍bfs求出终点的可到点（一定要等队列自然弹空而不是遇到起点就break（我简直是傻子）否则会有一些点无法遍历到）；然后标记所有可行的点，即出点都是可到的点；然后正着跑一边bfs，解决。

CF1237F Balanced Domino Placements：
借鉴CF题解，自己实在是愚蠢。
我们首先标记不能放置的行和列。
我们假设要先放a个水平骨牌，b个竖直骨牌，我们现在需要找到在n行中（除去有标记的列）放a个的方案，在m行中（除去有标记的列）放b个的方案。

其实这就是在一维数轴上面有一些禁止点，我们要在上面放 \(a\) 个长为2的线段，然后在剩下的可行点中随意选 \(b\) 个，
在另一维数轴上面也有一些禁止点，我们要在上面放 \(a\) 个长为2的线段，然后在剩下的可行点中随意选 \(a\) 个。注意匹配的方案数要乘上 \(b!\) 和 \(a!\) ，代表 \(b\) 个长为2的线段 和 剩下的可行点中随意选的 \(b\) 个 去进行随机配对。
如何求在一维数轴上面有一些禁止点，我们要在上面放 \(a\) 个长为2的线段呢？DP，\(f[i][j]=f[i-1][j]+(i>=2 \&\&\ !vis[i-1]\ \&\&\ !vis[i]:f[i-2][j-1])\)。

P1297 [国家集训队]单选错位：大水题。（记住不会的一幕）。

P5017 摆渡车：按时间轴DP，斜率优化。

P3564 [POI2014]BAR-Salad Bar 这种题就很考虑思维了
链表题？
先将 p,j 转化成 1,-1，然后做一遍前缀和。
首先有 \(sum[L]\leq sum[i]\ \&\&\ n-sum[R]\leq n-sum[i]\) ，即 \(sum[L]\leq sum[i] \leq sum[R],\ i \in [L,R]\) 。
我们设 \(nxt[i]\) 表示 \(sum[i]==sum[j],j>i\) 的最小的 \(j\) ，\(pre\) 指针表示当前点 \(i\) 往后的最后一个合法的 \(r\) 的位置，然后由于相邻两个前缀和的差最多为 1，所以不会出现类似右下图的情况。
然后结合代码。

inline void main() {
	n=g(); scanf("%s",s+1);
	for(R i=1;i<=n;++i) sum[i]=sum[i-1]+(s[i]=='p'?1:-1);
	for(R i=n;~i;--i) nxt[i]=lst[sum[i]],lst[sum[i]]=i,vr[i]=i;
	for(R i=n,pre=n;i;--i) {
		if(s[i]=='p') {//若是上升部分
			if(nxt[i-1]&&sum[vr[nxt[i-1]]]>=sum[pre]) pre=vr[nxt[i-1]];
			vr[i-1]=pre;
			ans=max(ans,pre-i+1);
		} else pre=i-1;//若是下降部分，即sum[i-1]>sum[i]
	} printf("%d\n",ans);
}

P3132 [USACO16JAN]愤怒的奶牛Angry Cows ：一眼二分，考虑如何ck。
\(f[i]\) 表示覆盖 \(1-i\) 的最小半径，\(h[i]\) 表示覆盖 \(i-n\) 的最小半径。我们只讨论 \(f[i]\)。
\(f[i]=min(f[i],max(f[j]+1,a[i]-a[j]),j<i\) ，这时如果要枚举就是 \(n^2\) 的。

但是我们发现，\(f[j]\) 随着 \(j\) 是单调不降的（莫非更大了半径还能更小？），而 \(a[i]-a[j]\) 是递减的。所以我们可知，最小值取在交点处。
而随着 \(i\) 的增大，\(a[i]-a[j]\) 会往上平移，导致交点单调向右移，所以我们维护一个指针即可 \(\mathcal{O}(n)\) 求出 \(f[]\) 。
类似这样：

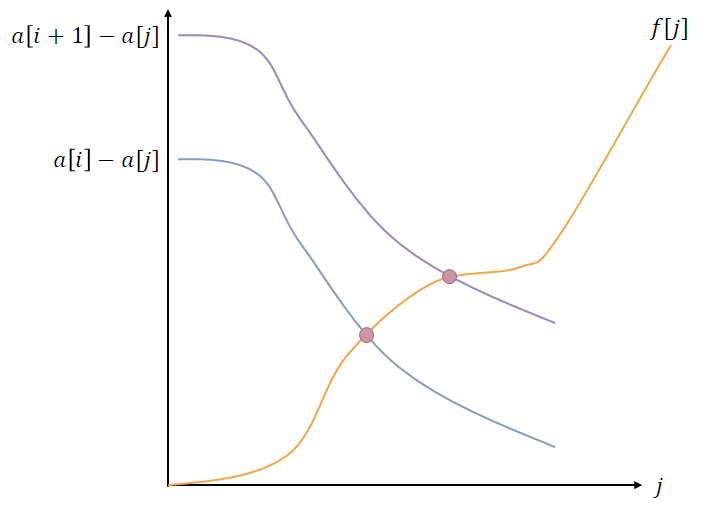
check时就找是否存在 \(i,j,i\leq j\) 且 \(f[i]+1\leq R,h[j]+1\leq R,a[j]-a[i]\leq 2R\) 即可。

inline bool ck(double x) { R p=n;
	for(R i=n;i;--i) if(f[i]+1<=x) {
		while(a[p]-a[i]>2*x) --p;
		if(h[p]+1<=x) return true;
	} return false;
}
inline void main() {
	n=g(); for(R i=1;i<=n;++i) a[i]=g();
	sort(a+1,a+n+1); R p=1;
	for(R i=2;i<=n;++i) {
		while(p<i-1&&f[p]+1<a[i]-a[p]) ++p;
		f[i]=max(f[p]+1,a[i]-a[p]); 
	} 
	p=n;
	for(R i=n-1;i;--i) {
		while(i+1<p&&h[p]+1<a[p]-a[i]) --p;
		h[i]=max(h[p]+1,a[p]-a[i]);
	}
	register double l=0,r=a[n]+1,md;
	while(l+eps<r) {
		md=(l+r)/2;
		if(ck(md)) r=md;
		else l=md;
	} printf("%.1f\n",l);
}

P1627 [CQOI2009]中位数：把 \(<b\) 的看做 \(-1\) ,\(>b\) 的看做 \(1\), 左边开个桶，右边看一下。

int n,v,p,a[N],d[N<<1],*c=d+N; ll ans;
inline void main() {
	n=g(),v=g();
	for(R i=1;i<=n;++i) (a[i]=g())==v?p=i:0; c[0]=1;//注意0一开始就有（什么也不选）
	for(R i=p-1,t=0;i;--i) t+=a[i]>v?1:-1,++c[t];
	for(R i=p+1,t=0;i<=n;++i) t+=a[i]>v?1:-1,ans+=c[0-t];
	printf("%lld\n",ans+c[0]);
}

P3295 [SCOI2016]萌萌哒 ：并查集，倍增维护每个区间，拆成 \(log(n)\)，下放时注意标号的变化。
注意代码的写法比较氢气：

int n,m,tot,B;
int fa[17][N],lg[N];
inline int getf(int t,int x) {return x==fa[t][x]?x:fa[t][x]=getf(t,fa[t][x]);}
inline void merge(int t,int u,int v) {
	if(getf(t,u)!=getf(t,v)) fa[t][fa[t][u]]=fa[t][v];
}
inline int qpow(int a,int b) { R ret=1; if(b<0) return 0;
	for(;b;b>>=1,a=1ll*a*a%M) if(b&1) ret=1ll*ret*a%M; return ret;
}
inline void main() {
	n=g(),m=g(); for(R i=2;i<=n;++i) lg[i]=lg[i>>1]+1; B=lg[n];
	for(R t=0;t<=B;++t) for(R i=1,lim=n-(1<<t)+1;i<=n;++i) fa[t][i]=i;
	//注意每个块的fa是最开头的代表元素。 
	for(R i=1;i<=m;++i) { 
		R l1=g(),r1=g(),l2=g(),r2=g();
		for(R t=lg[r1-l1+1];~t;--t) if(l1+(1<<t)-1<=r1) 
			merge(t,l1,l2),l1+=(1<<t),l2+=(1<<t);
			//二进制拆分的思想 
	} 
	for(R t=B;t;--t) for(R i=1,lim=n-(1<<t)+1;i<=lim;++i) 
		merge(t-1,i,getf(t,i)),merge(t-1,i+(1<<t-1),fa[t][i]+(1<<t-1));
		//注意是fa[t][j]+(1<<t-1)，因为代表元素变了。 
	for(R i=1;i<=n;++i) if(getf(0,i)==i) ++tot; 	
	printf("%d\n",9ll*qpow(10,tot-1)%M);
}

P2868 [USACO07DEC]观光奶牛Sightseeing Cows：最优比率环，把点权放在边上（其实觉得很迷）。

inline bool spfa(int u) {
	vis[u]=true;
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(d[v]>d[u]+w[i]) {
			d[v]=d[u]+w[i];
			if(vis[v]) return vis[u]=false,true;
			if(spfa(v)) return vis[u]=false,true;
		}
	} return vis[u]=false;
}
inline bool ck(double x) {
	memset(d,0x42,sizeof d); //其实赋初值为0
	for(R i=1;i<=cnt;++i) w[i]=x*mem[i]-c[vr[i]];//边权
	for(R i=1;i<=n;++i) if(spfa(i)) return true;
	return false;
}
inline void main() {
	n=g(),m=g(); 
	for(R i=1;i<=n;++i) c[i]=g();
	for(R i=1,u,v,w;i<=m;++i) u=g(),v=g(),w=g(),add(u,v,w);
	register double l=0,r=1000000,md;
	while(l+eps<r) {
		md=(l+r)/2;
		if(ck(md)) l=md;
		else r=md;
	} printf("%.2f\n",l);
}

CF413E Maze 2D：线段树乱搞，维护区间左边两个点到右边两个点的距离。

int m,q; bool s[K][N]; char str[N];
struct node { int d[K][K]; 
	inline int* operator [] (const int& src) {return d[src];}
	inline node operator + (const node& that) const {
		register node ret; memset(ret.d,Inf,SZ);
		for(R i=0;i<K;++i) for(R j=0;j<K;++j) for(R k=0;k<K;++k) 
			ret.d[i][j]=min(ret.d[i][j],d[i][k]+that.d[k][j]+1);//更新最短路
		return ret;
	}
}t[N<<2];
#define ls (tr<<1)
#define rs (tr<<1|1)
inline void pre(int tr,int l) { memset(t[tr].d,Inf,SZ);
	for(R i=0;i<K;++i) for(R j=i;j<K;++j) if(s[j][l])
		t[tr][i][j]=t[tr][j][i]=j-i; else break; //初始化
} 
inline void build(int tr,int l,int r) {
	if(l==r) return pre(tr,l); R md=l+r>>1; 
	build(ls,l,md),build(rs,md+1,r); t[tr]=t[ls]+t[rs];
}
inline node query(int tr,int l,int r,int LL,int RR) {
	if(LL<=l&&r<=RR) return t[tr]; R md=l+r>>1;
	if(LL>md) return query(rs,md+1,r,LL,RR);
	else if(RR<=md) return query(ls,l,md,LL,RR);
	else return query(ls,l,md,LL,RR)+query(rs,md+1,r,LL,RR);
}
inline void main() { m=g(),q=g();
	for(R i=0;i<K;++i) { scanf("%s",str+1); 
		for(R j=1;j<=m;++j) s[i][j]=str[j]=='.';
	} build(1,1,m);
	while(q--) { 
		R x=g(),y=g(); R a=(x-1)/m,b=(x-1)%m+1,c=(y-1)/m,d=(y-1)%m+1;
		if(b>d) swap(b,d),swap(a,c);
		x=query(1,1,m,b,d).d[a][c],
		printf("%d\n",x!=Inf?x:-1);	
	}
}

P2466 [SDOI2008]Sue的小球：正难则反，我们区间DP失去的最小代价，类似关路灯。

struct node { int x,y,v;
	inline bool operator < (const node& that) const 
		{return x<that.x;}
}a[N];
int n,x0; ll f[N][N][2],s[N],ans;
inline void main() {
	n=g(),x0=g(); for(R i=1;i<=n;++i) a[i].x=g();
	for(R i=1;i<=n;++i) a[i].y=g(),ans+=a[i].y;
	for(R i=1;i<=n;++i) a[i].v=g(); a[++n].x=x0;//要把初始点加进去
	sort(a+1,a+n+1); memset(f,0x3f,sizeof f);
	for(R i=1;i<=n;++i) if(a[i].x==x0&&a[i].y==0&&a[i].v==0) 
		f[i][i][0]=f[i][i][1]=0;//初值 
	for(R i=1;i<=n;++i) s[i]=s[i-1]+a[i].v;//前缀和
	for(R l=1;l<=n;++l) for(R i=1,j=l;j<=n;++i,++j) {
		f[i][j][0]=min(f[i][j][0],f[i+1][j][0]+(s[n]-s[j]+s[i])*(a[i+1].x-a[i].x));
		f[i][j][1]=min(f[i][j][1],f[i][j-1][1]+(s[n]-s[j-1]+s[i-1])*(a[j].x-a[j-1].x));
		f[i][j][0]=min(f[i][j][0],f[i+1][j][1]+(s[n]-s[j]+s[i])*(a[j].x-a[i].x));
		f[i][j][1]=min(f[i][j][1],f[i][j-1][0]+(s[n]-s[j-1]+s[i-1])*(a[j].x-a[i].x));
	} printf("%.3f\n",(ans-min(f[1][n][0],f[1][n][1]))/1000.0);
}

P1848 [USACO12OPEN]书架Bookshelf：首先有暴力DP的式子：
\(f[i]=\min(f[i],f[j]+\max(h[j],h[j+1],\cdots,h[i])),j\ 满足\ \sum_{k=j+1}^i w[k] \leq L\)
如何优化？发现 \(\max\) 很难受，于是我们可以处理出每个点 \(i\) 能作为最大值的最左端点 \(pre[i]\)，然后我们每插入一个 \(h[i]\) ，就将\([pre[i],i]\) 的 \(\max\) 修改成 \(h[i]\) （相当于对 \(\max\) 区间推平） ；现在还有一个取 \(\min\) ；于是我们可以用线段树维护以上两种操作，线段树中分开维护 \(\max\) 和 \(f[i]\) 。注意找合法区间时，可二分，也可以单调指针。

int n,L,h[N],w[N],stk[N],pre[N],top;
ll mn[N<<2],tg[N<<2],vl[N<<2],f[N],sum[N];
inline void spread(int tr) {
	mn[ls]=tg[tr]+vl[ls],mn[rs]=tg[tr]+vl[rs];
	tg[ls]=tg[rs]=tg[tr],tg[tr]=-1;
}
inline void change(int tr,int l,int r,int LL,int RR,int d) {
	if(LL<=l&&r<=RR) return tg[tr]=d,mn[tr]=vl[tr]+d,void();
	R md=l+r>>1; if(~tg[tr]) spread(tr);
	if(LL<=md) change(ls,l,md,LL,RR,d);
	if(RR>md) change(rs,md+1,r,LL,RR,d);
	mn[tr]=min(mn[ls],mn[rs]),vl[tr]=min(vl[ls],vl[rs]);
}
inline void change(int tr,int l,int r,int p) {
	if(l==r) return mn[p]=Inf,vl[tr]=f[p-1],void(); R md=l+r>>1;
	if(~tg[tr]) spread(tr); 
	if(p<=md) change(ls,l,md,p); if(p>md) change(rs,md+1,r,p);
	mn[tr]=min(mn[ls],mn[rs]),vl[tr]=min(vl[ls],vl[rs]);
}
inline ll query(int tr,int l,int r,int LL,int RR) {
	if(LL<=l&&r<=RR) return mn[tr]; R md=l+r>>1;
	if(~tg[tr]) spread(tr); register ll ret=Inf;
	if(LL<=md) ret=query(ls,l,md,LL,RR);
	if(RR>md) ret=min(query(rs,md+1,r,LL,RR),ret); return ret;
}
inline void main() {
	memset(mn,0x3f,sizeof mn),
	memset(vl,0x3f,sizeof vl),
	memset(tg,0xff,sizeof tg);
	n=g(),L=g(); for(R i=1;i<=n;++i) h[i]=g(),w[i]=g();
	for(R i=1;i<=n;++i) sum[i]=sum[i-1]+w[i];
	h[0]=2e9; stk[++top]=0;
	for(R i=1;i<=n;++i) {
		while(h[i]>h[stk[top]]) --top;
		pre[i]=stk[top]+1; stk[++top]=i;
	}
	for(R i=1;i<=n;++i) {
		change(1,1,n,i);
		change(1,1,n,pre[i],i,h[i]);		
		R pos=lower_bound(sum,sum+i+1,sum[i]-L)-sum;
		if(pos<i) f[i]=query(1,1,n,pos+1,i);
	} printf("%lld\n",f[n]);
}

P2579 [ZJOI2005]沼泽鳄鱼：我们发现 \(2,3,4\) 的 \(lcm\) 只有 \(12\) ，于是预处理出整 \(12\) 单位时间的转移矩阵，同时保留散的转移矩阵。整 \(12\) 的快速幂，不整的暴力。

int n,m,s,t,k,a[L+1][N][N],c[L],ans[N][N];
inline void mul(int a[N][N],int b[N][N]) {
	R ret[N][N]; memset(ret,0,sizeof ret);
	for(R i=1;i<=n;++i) for(R k=1;k<=n;++k) if(a[i][k])
		for(R j=1;j<=n;++j) ret[i][j]=(ret[i][j]+1ll*a[i][k]*b[k][j])%M;
	memcpy(a,ret,sizeof ret);
}
inline void qpow(int a[N][N],int b) { 
	R ret[N][N]; memset(ret,0,sizeof ret); 
	for(R i=1;i<=n;++i) ret[i][i]=1;
	for(;b;b>>=1,mul(a,a)) if(b&1) mul(ret,a); 
	memcpy(a,ret,sizeof ret);
}
inline void main() {
	n=g(),m=g(),s=g()+1,t=g()+1,k=g();
	for(R i=1,u,v;i<=m;++i) u=g()+1,v=g()+1,a[1][u][v]=a[1][v][u]=1;
	for(R i=2;i<=L;++i) memcpy(a[i],a[1],sizeof a[1]); m=g(); 
	for(R i=1,t;i<=m;++i) { t=g(); 
		for(R j=1;j<=t;++j) c[j]=g()+1; 
		for(R k=1;k<=L;++k) for(R v=1;v<=n;++v)
			a[k][v][c[k%t+1]]=0;
	} for(R i=1;i<=n;++i) ans[i][i]=1;
	for(R i=1;i<=L;++i) mul(ans,a[i]);
	qpow(ans,k/L); for(R i=1;i<=k%L;++i) mul(ans,a[i]);
	printf("%d\n",ans[s][t]);
}

P2396 yyy loves Maths VII：卡常好题（雾）。数据范围小，又不能搜索，于是状压。
\(f[S]\) 表示数集中的选或没选的状态，然后就正常转移即可，注意，若当前 \(\sum_{i\in S} a[i] = 厄运数字\) ，就不能转移。

const int L=24,M=1000000007;
int n,m,d1,d2,dis[1<<L],f[1<<L];
inline void main() {
	n=g(); for(R i=0;i<n;++i) dis[1<<i]=g(); d1=d2=-1;
	m=g(); if(m) {d1=g(); if(m-1) d2=g();} f[0]=1;
	for(R i=1,lim=1<<n;i<lim;++i) { R lbt=i&-i,l;
		dis[i]=dis[i^lbt]+dis[lbt];
		if(dis[i]==d1||dis[i]==d2) continue;
		lbt=i; while(lbt) {	l=lbt&-lbt; f[i]+=f[i^l]; 
			if(f[i]>=M) f[i]-=M; lbt^=l; 	
		}
	} printf("%d\n",f[(1<<n)-1]);
}

CF1175F The Number of Subpermutations：转化题意：每个数 \(a[i],l\leq i\leq r\) 的 \(nxt[a[i]]>r\)
考虑最大值分治，这样我们可以直接获得区间长度。然后每次枚举小的一边。用ST表查区间 \(nxt[]\) 的最小值。

const int N=300010,B=18;
int n,ans,lg[N],lst[N],a[N],stk[N],ls[N],rs[N],top,mn[N][B+1];
inline int qmin(int l,int r) { R t=lg[r-l+1]; 
	return min(mn[l][t],mn[r-(1<<t)+1][t]);
}
inline void solve(int l,int r,int p) { 	R t=a[p];
	if(p-l<r-p) { R LL=max(p-t+1,l),RR=min(p,r-t+1);
		for(R i=LL;i<=RR;++i) if(qmin(i,i+t-1)>i+t-1) ++ans;
	} else { R LL=max(p,l+t-1),RR=min(r,p+t-1);
		for(R i=LL;i<=RR;++i) if(qmin(i-t+1,i)>i) ++ans;
	} if(ls[p]) solve(l,p-1,ls[p]);
	if(rs[p]) solve(p+1,r,rs[p]);
}
inline void main() {
	n=g(); stk[++top]=0,a[0]=1e9;
	for(R i=2;i<=n;++i) lg[i]=lg[i>>1]+1;
	for(R i=1,l;i<=n;++i) { l=0;
		a[i]=g(),mn[lst[a[i]]][0]=i,lst[a[i]]=i;
		while(a[stk[top]]<a[i]) l=stk[top],--top;
		ls[i]=l,rs[stk[top]]=i,stk[++top]=i;
	} for(R i=1;i<=n;++i) mn[lst[a[i]]][0]=n+1;
	for(R t=1;t<=B;++t) for(R i=1,k=1+(1<<t-1),lim=n-(1<<t)+1;i<=lim;++i,++k) 
		mn[i][t]=min(mn[i][t-1],mn[k][t-1]);
	solve(1,n,stk[2]); printf("%d\n",ans);
}

P2219 [HAOI2007]修筑绿化带：单调队列。
框住一个 \(A*B\) 的矩形后，我们就是要在他里面找到一个位置使得对应的 \(C*D\) 的矩形的值最小即可。最小值可以单调队列维护；当然这种题也可以二维ST表。(注意代码中的 \(A,B\) 与 \(C,D\) 是反的)

const int N=1010;
int n,m,A,B,C,D,ans,s[N][N],s1[N][N],s2[N][N];
deque<int> q[N],p;
inline void main() {
	n=g(),m=g(),C=g(),D=g(),A=g(),B=g();
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s[i][j]=g();
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s[i][j]+=s[i][j-1];
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s[i][j]+=s[i-1][j];
	for(R i=A;i<=n;++i) for(R j=B;j<=m;++j) s1[i][j]=s[i][j]-s[i-A][j]-s[i][j-B]+s[i-A][j-B];
	for(R i=C;i<=n;++i) for(R j=D;j<=m;++j) s2[i][j]=s[i][j]-s[i-C][j]-s[i][j-D]+s[i-C][j-D];
	for(R i=A;i<C;++i) for(R j=B;j<=m;++j) {
		while(q[j].size()&&s1[q[j].back()][j]>=s1[i][j]) q[j].pop_back();
		q[j].push_back(i);
	}
	for(R i=C;i<=n;++i) {
		p.clear();
		for(R j=B;j<D;++j) {
			while(p.size()&&s1[q[p.back()].front()][p.back()]>=s1[q[j].front()][j]) p.pop_back();
			p.push_back(j);
		} 
		for(R j=D;j<=m;++j) {
			while(p.size()&&p.front()<B+j-D+1) p.pop_front();
			ans=max(s2[i][j]-s1[q[p.front()].front()][p.front()],ans);
			while(p.size()&&s1[q[p.back()].front()][p.back()]>=s1[q[j].front()][j]) p.pop_back();
			p.push_back(j); 
		}
		for(R j=B;j<=m;++j) {
			while(q[j].size()&&q[j].front()<A+i-C+2) q[j].pop_front();
			while(q[j].size()&&s1[q[j].back()][j]>=s1[i][j]) q[j].pop_back();
			q[j].push_back(i);
		} 
	} printf("%d\n",ans);
}

P4755 Beautiful Pair：最大值分治。
还是知道最大值后就枚举 \(sz\) 比较小的一边，然后用主席树维护区间的权值线段树，在上面二分查找 \(\leq \frac{mx}{a[i]}\) 的数量。

const int N=100010,B=16;
int n,cnt,L,a[N],b[N],stk[N],top; ll ans;
int sz[N*B*B],ls[N*B*B],rs[N*B*B],lc[N],rc[N],rt[N];
inline void change(int& tr,int t,int l,int r,int p) {
	tr=++cnt; sz[tr]=sz[t]+1,ls[tr]=ls[t],rs[tr]=rs[t];
	if(l==r) return ; R md=l+r>>1;
	if(p<=md) change(ls[tr],ls[t],l,md,p);
	if(p>md) change(rs[tr],rs[t],md+1,r,p);
}
inline int query(int tr,int t,int l,int r,int k) {
	if(!tr) return 0; if(l==r) return b[l]<=k?sz[tr]-sz[t]:0; R md=l+r>>1; 
	if(k<=b[md]) return query(ls[tr],ls[t],l,md,k);
	if(k>b[md]) return sz[ls[tr]]-sz[ls[t]]+query(rs[tr],rs[t],md+1,r,k); 
}
inline void solve(int l,int r,int tr) { 
	if(tr-l<r-tr) for(R i=l;i<=tr;++i) ans+=query(rt[r],rt[tr-1],1,L,a[tr]/a[i]);
	else for(R i=tr;i<=r;++i) ans+=query(rt[tr],rt[l-1],1,L,a[tr]/a[i]);
	if(lc[tr]) solve(l,tr-1,lc[tr]); if(rc[tr]) solve(tr+1,r,rc[tr]);
}
inline void main() {
	cnt=n=g(); top=1,a[0]=2e9;
	for(R i=1;i<=n;++i) { R lst=0; a[i]=g(); 
		while(a[stk[top]]<=a[i]) lst=stk[top],--top;
		lc[i]=lst,rc[stk[top]]=i,stk[++top]=i;
	} memcpy(b,a,sizeof b); 
	sort(b+1,b+n+1); L=unique(b+1,b+n+1)-b-1; 
	for(R i=1,p;i<=n;++i) {
		p=lower_bound(b+1,b+L+1,a[i])-b;
		change(rt[i],rt[i-1],1,L,p); 
	} solve(1,n,rc[0]),printf("%lld\n",ans);
}

P1655 小朋友的球：递推+高精。
\(f[n][m]=f[n-1][m]*m+f[n-1][m-1]\)

const int N=100;
const int B=10000,L=4; 
struct Int {
#define SIZE 510
	int a[SIZE],sz;
	Int() {sz=0,memset(a,0,sizeof a);}
	inline int& operator [](const int& src) {return a[src];}
	inline Int operator = (int x) {
		sz=0,memset(a,0,sizeof a);
		while(x) a[++sz]=x%B,x/=B;
		return *this;
	}
	inline bool operator < (Int that) const {
		if(sz!=that.sz) return sz<that.sz;
		for(R i=sz;i>=1;--i) if(a[i]!=that[i]) return a[i]<that[i];
		return 0;
	}
	inline Int operator + (Int that) const {
		register Int ret=*this; ret.sz=max(ret.sz,that.sz)+1;
		for(R i=1;i<=ret.sz;++i) {
			ret[i]+=that[i];
			if(ret[i]>=B) ++ret[i+1],ret[i]-=B;
		} while(!ret[ret.sz]&&ret.sz) --ret.sz;
		return ret;
	}
	inline Int operator * (const int& that) const {
		register Int ret=*this; 
		for(R i=1;i<=ret.sz;++i) ret[i]*=that;
		for(R i=1;i<=ret.sz;++i) ret[i+1]+=ret[i]/B,ret[i]%=B;
		while(ret[ret.sz]) ++ret.sz,ret[ret.sz+1]=ret[ret.sz]/B,ret[ret.sz]%=B;
		return ret;
	}
	inline void print() { printf("%d",a[sz]);
		for(R i=sz-1;i>=1;--i) printf("%04d",a[i]); puts("");
	}
}f[N+10][N+10];
int n,m;
inline void main() {
	f[0][0]=1; for(R i=1;i<=N;++i) for(R j=1;j<=i;++j) 
		f[i][j]=f[i-1][j-1]+f[i-1][j]*j;
	while(~scanf("%d%d",&n,&m)) {
		if(!n||n<m) {puts("0"); continue;}
		f[n][m].print(); 
	}
}

P4910 帕秋莉的手环：矩阵快速幂。设\(f[i][0/1]\) 表示填到第 \(i\) 位末尾是 黑 or 白的方案数。（两个白的不能相连）

\(f[i][0]=f[i-1][1],f[i][1]=f[i-1][0]+f[i-1][1]\)

然后我们强制第一位是黑的，这样最后答案即为 \(f[n][0]*2+f[n][1]\)，相当于 黑白，白黑（这两种是一样的）和 黑黑。

const int N=2,M=1000000007,mem[2][2]={{0,1},{1,1}},A[2][2]={{0,1},{0,0}};
int T,a[N][N],ans[N][N]; ll n;
inline void mul(int a[N][N],int b[N][N]) {
	R ret[N][N]; memset(ret,0,sizeof ret);
	for(R i=0;i<N;++i) for(R k=0;k<N;++k) for(R j=0;j<N;++j)
		ret[i][j]=(ret[i][j]+1ll*a[i][k]*b[k][j])%M;
	memcpy(a,ret,sizeof ret);
}
inline void qpow(int a[N][N],ll b) {
	R ret[N][N]; memset(ret,0,sizeof ret);
	for(R i=0;i<N;++i) ret[i][i]=1;
	for(;b;b>>=1,mul(a,a)) if(b&1) mul(ret,a); 
	memcpy(a,ret,sizeof ret); 
}
inline void main() {
	T=g(); while(T--) {
		n=g(); memcpy(a,mem,sizeof mem),memcpy(ans,A,sizeof A);
		qpow(a,n-1),mul(ans,a); 
		printf("%d\n",(2ll*ans[0][0]+ans[0][1])%M);
	}
}

P3430 [POI2005]DWU-Double-row：二分图。
本质上来看，我们设每列最终的状态为 \(f[i]=0/1\)，表示 不交换/上下交换 ，我们相当于给了一些 \(f[i]\) 之间的关系：\(f[i]==f[j]\) 则 \(i,j\) 之间连 \(0\) 边；\(f[i]!=f[j]\) 则 \(i,j\) 之间连 \(1\) 边。

根据以上结论，我们将 在同一行的相同的两个数所在的列连 \(1\) 边，表示两列的状态最终是不同的；不在同一行的两个相同的数之间连 \(0\) 边，表示两列最后的状态是相同的。

然后遍历整张图的每个连通块，进行染色。每个连通块的答案即 \(\min(黑点数目,白点数目)\)，因为我们可以选择翻转黑点，也可以翻转白点 。最终的答案为每个连通块的答案之和，因为连通块之间没有影响。

const int N=50010;
int n,m,cnt,ans,t1,t2,a[N],b[N],v1[N<<1],v2[N<<1];
int vr[N<<1],nxt[N<<1],fir[N<<1],w[N<<1],c[N];
inline void add(int u,int v,int ww) {
	vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;
	vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt,w[cnt]=ww;
}
inline void dfs(int u,int C) { 
	c[u]=C; t1+=C,t2+=(C^1);	
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(~c[v]) continue; dfs(v,C^w[i]);
	}
}
inline void main() { 
	n=g(); memset(c,0xff,sizeof c);
	for(R i=1;i<=n;++i) { a[i]=g(); 
		if(v1[a[i]]) add(v1[a[i]],i,1); v1[a[i]]=i;
	} 
	for(R i=1;i<=n;++i) { b[i]=g(); 
		if(v1[b[i]]) add(v1[b[i]],i,0);
		if(v2[b[i]]) add(v2[b[i]],i,1); v2[b[i]]=i;
	} for(R i=1;i<=n;++i) if(c[i]==-1) t1=0,t2=0,dfs(i,0),ans+=min(t1,t2);
	printf("%d\n",ans);
}

P4167 [Violet]樱花：拆式子。
\(xy-(x+y)n!=0 \rightarrow xy-(x+y)n!+(n!)^2=(n!)^2 \rightarrow (x-n!)(y-n!)=(n!)^2\)
所以我们只要确定有多少个 \((x-n!)\) 和 \((y-n!)\) 即可，或者，我们只确定一边，另一边就确定了，那么答案就是 \(n!\) 的约数个数。

const int N=1e6+10,M=1e9+7;
int n,ans=1,cnt,mnd[N],p[N/2],v[N],c[N/2];
inline void PRE() {
	for(R i=2;i<=n;++i) {
		if(!v[i]) p[++cnt]=i,mnd[i]=cnt;
		for(R j=1;j<=cnt&&i*p[j]<=n;++j) {
			v[i*p[j]]=true; mnd[i*p[j]]=j;
			if(i%p[j]==0) break;
		}
	}
}
inline void main() {
	n=g(); PRE(); for(R i=2;i<=n;++i) { R x=i;
		while(x>1) ++c[mnd[x]],x/=p[mnd[x]];
	} for(R i=1;i<=cnt;++i) ans=1ll*ans*(2*c[i]+1)%M;
	printf("%d\n",ans); 
}

CF893F Subtree Minimum Query：dfs序实现子树限制，按深度建立前缀主席树实现深度限制。

const int N=100010,B=19,Inf=0x3f3f3f3f;
int n,m,r,cnt,tot,num,L,ans,rt[N];
int vr[N<<1],nxt[N<<1],fir[N],w[N<<1],c[N],d[N],a[N],dfn[N],low[N];
int ls[N*B],rs[N*B],mn[N*B];
inline void add(int u,int v) {
	vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;
	vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt;
}
inline bool cmp(const int& _this,const int& _that) 
	{return d[_this]<d[_that];}
inline void dfs(int u) { dfn[u]=++num;
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(d[v]) continue; d[v]=d[u]+1; dfs(v);
	} low[u]=num;
}
inline void change(int& tr,int t,int l,int r,int p,int v) {
	tr=++tot,mn[tr]=min(mn[t],v),ls[tr]=ls[t],rs[tr]=rs[t]; 
	if(l==r) return ; R md=l+r>>1; 
	if(p<=md) change(ls[tr],ls[t],l,md,p,v);
	if(p>md) change(rs[tr],rs[t],md+1,r,p,v);
}
inline int query(int tr,int l,int r,int LL,int RR) { 
	if(LL<=l&&r<=RR) return mn[tr]; R md=l+r>>1,ret=Inf;
	if(LL<=md&&ls[tr]) ret=query(ls[tr],l,md,LL,RR);
	if(RR>md&&rs[tr]) ret=min(ret,query(rs[tr],md+1,r,LL,RR)); return ret;
}
inline void main() { memset(mn,0x3f,sizeof mn);
	n=g(),r=g(); for(R i=1;i<=n;++i) c[i]=g();
	for(R i=1,u,v;i<n;++i) u=g(),v=g(),add(u,v);
	for(R i=1;i<=n;++i) a[i]=i; d[r]=1,dfs(r);
	sort(a+1,a+n+1,cmp); L=d[a[n]];
	for(R i=1;i<=n;++i) 
		change(rt[d[a[i]]],rt[d[a[i-1]]],1,n,dfn[a[i]],c[a[i]]);
	m=g(); for(R i=1,u,k;i<=m;++i) u=g(),k=g(),u=(ans+u)%n+1,k=(ans+k)%n,
		printf("%d\n",ans=query(rt[min(d[u]+k,L)],1,n,dfn[u],low[u]));
}