树状数组

树状数组本质：支持单点修改的快速前缀和（单点修改，区间查询）

题目：acwing241

 

在完成了分配任务之后，西部 314314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 nn 个点，经测量发现这 nn 个点的水平位置和竖直位置是两两不同的。

西部 314314 认为这幅壁画所包含的信息与这 nn 个点的相对位置有关，因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)(1,y1),(2,y2),…,(n,yn)，其中 y1∼yny1∼yn 是 11 到 nn 的一个排列。

西部 314314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 (i,yi),(j,yj),(k,yk)(i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n1≤i<j<k≤n 且 yi>yj,yj<ykyi>yj,yj<yk，则称这三个点构成 V 图腾;

如果三个点 (i,yi),(j,yj),(k,yk)(i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n1≤i<j<k≤n 且 yi<yj,yj>ykyi<yj,yj>yk，则称这三个点构成 ∧ 图腾;

西部 314314 想知道，这 nn 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long LL;

const int N = 200010;
int n,m,a[N];
int gr[N],lo[N],tr[N];

int lowbit(int x){
    return x&-x;//返回非负整数x在二进制表示下最低位1及其后面的0构成的数值
}
//将序列中第x个数加上k。
void add(int x,int t){
    for (int i = x; i <= n; i += lowbit(i) )tr[i]+=t;
}
//查询序列前x个数的和
int ask(int x){
    int sum=0;
    for (int i = x; i ; i -=lowbit(i) )
        sum+=tr[i];
    return sum;
}

int main()
{
    cin>>n;
    for (int i = 1; i <= n; i ++ )
        cin>>a[i];
    //从左向右，依次统计每个位置左边比第i个数y小的数的个数、以及大的数的个数
    for (int i = 1; i <= n; i ++ ){
        int y=a[i];
        lo[i]=ask(y-1);//在前面已加入树状数组的所有数中统计在区间[1, y - 1]的数字的出现次数
        gr[i]=ask(n)-ask(y);
        add(y,1);
    }
    
    LL res1=0,res2=0;
    memset(tr, 0, sizeof tr);//从右向左再来一次
    for (int i = n; i >=1 ; i -- ){
        int y=a[i];
        res1+=(LL)gr[i]*(ask(n)-ask(y));
        res2+=(LL)lo[i]*(ask(y-1));
        add(y,1);
    }
    
    cout<<res1<<" "<<res2;
    return 0;
}

 

 

树状数组

 

 

 

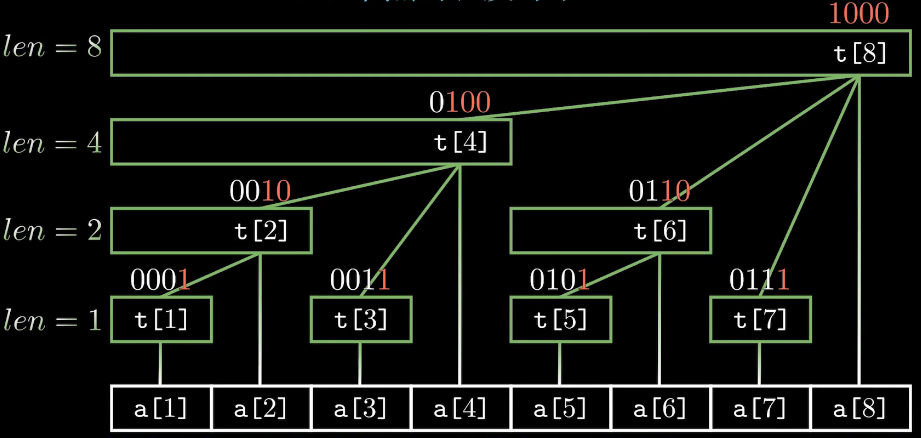
1，每个结点t[x]保存以x为根的子树中叶结点值的和
2，每个结点覆盖的长度为lowbit(x)
3，t[x]结点的父结点为t[x + lowbit(x)]
4，树的深度为log2n+1

树状数组操作
add(x, k)表示将序列中第x个数加上k。

以add(3, 5)为例：

 

 

 

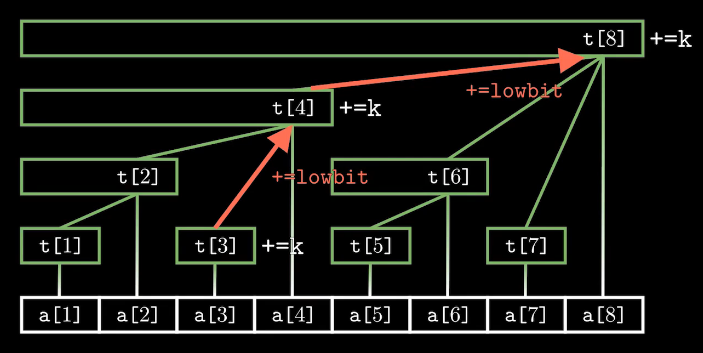
在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的t[x]值都加上k，这样保证计算区间和时的结果正确。时间复杂度为O(logn)O(logn)。

 

ask(x)表示将查询序列前x个数的和

 

 

 

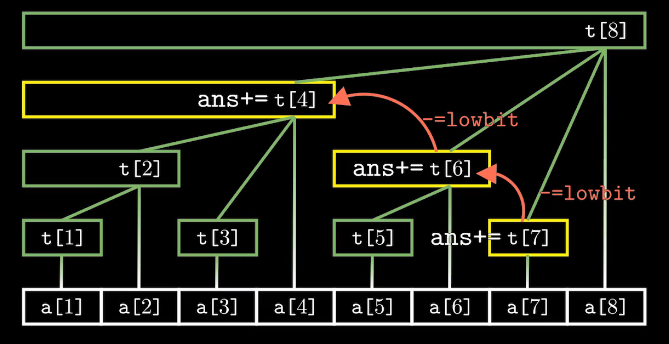
以ask(7)为例：
查询这个点的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值。向左上找到上一个结点，只需要将下标 x -= lowbit(x)，例如 7 - lowbit(7) = 6。