Tarjan 缩点 ：（洛谷 P3387 【模板】缩点）

在洛谷中查看

---

Tarjan 介绍：

Tarjan 大致有两种，有向图中的 与 无向图中的。

• 有向图中：求得是 缩点
• 无向图中：求得是 割点与桥

此文介绍的是有向图中的 缩点。

\(dfn\) 表示遍历到这个点的时间（这个时间的定义就是 Tarjan 被调用的次数）。
\(low\) 表示这个点，它能到的点中 \(dfn\) 最小的是多少。

给你个图看看，我们默认遍历是从 \(1\) ~ \(n\) 的。

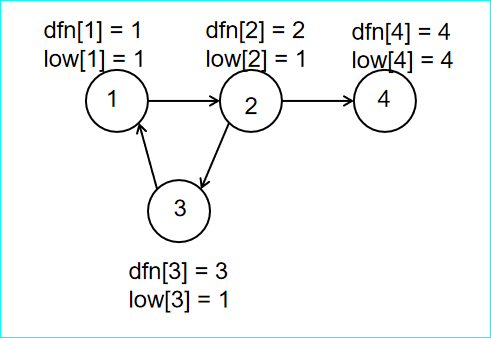
注：有向图 与 无向图 中 \(dfn\) 和 \(low\) 的定义有所不同。

---

Tarjan 模拟：

突然感觉 Tarjan 很神奇。我想给大家模拟一遍，然后希望能让大家更好理解。（了解一下代码再看看图解哦~）

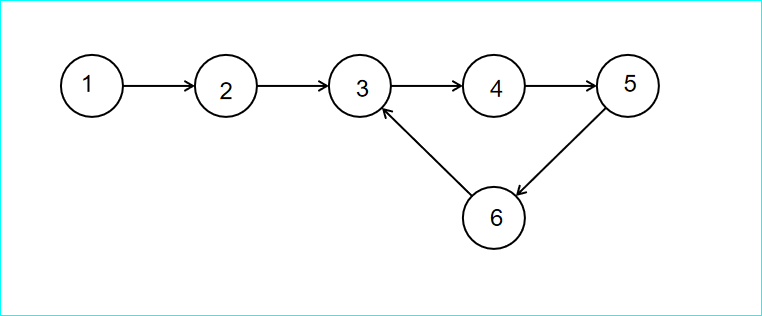
不断递归，从点 \(1\) 到点 \(6\)。

到点 \(6\) 时发现点 \(3\) 到过了，那么不再递归。此时 \(low[6]\) 为 \(3\)，不会划分强连通。

回溯到点 \(5\) ,\(low[5]\) 为 \(3\),不会划分强连通。点 \(4\) 同理。

直到回溯到点 \(3\)，\(dfn[3] = low[3]\)，所以划分强连通。点 \(2\)、点 \(1\) 一样。

---

所以如果能够强连通，\(low\) 必然被更新掉了，\(dfn = low\) 的情况只会有一次。

如果不能够强连通（就自己一个点在一个强连通里），\(dfn = low\) 也只有一次。

真的很神奇，很巧妙啊。

---

对喽，还有一些难理解的地方简单讲一下。

• else if(!col[t])low[x]=min(low[x],dfn[t]); 这句话改为 low[x]=min(low[x],low[t]); 在缩点模板中是可行的，但在求割点和桥里是不行的，因为：如果这个点是割点，那么说明这个点能到的子图里（不止一个子图） 没有其他的边连着它们。我在无向图模板中会给图的，期待一下吧。

所有思考都在代码，可以结合代码思考。谢谢观看~

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5;
int n, m, val[N];
int dfn[N], low[N], num, col[N], cnt;
//col 记录每个点属于哪个联通分量 
//num 记录遍历时间    cnt 记录缩点完后有多少个点 
int st[N], top;
queue<int> q;
int new_val[N], du[N], f[N], ans;
vector<int> g[N], new_g[N];
inline int read() {
	int s = 0, f = 1; char c = getchar();
	while (c < '0' || c>'9') { if (c == '-')f = -1; c = getchar(); }
	while (c >= '0' && c <= '9') { s = (s << 1) + (s << 3) + (c ^ 48); c = getchar(); }
	return s * f;
}
void tarjan(int x) {
	dfn[x] = low[x] = ++num; st[++top] = x;//更新这个点 
	for (int i = 0; i < g[x].size(); i++) {
		int t = g[x][i];
		if (!dfn[t])tarjan(t), low[x] = min(low[x], low[t]);//往下更新（要确保下个点没被更新） 
		else if (!col[t])low[x] = min(low[x], dfn[t]);//被更新了，但没被划分到强连通分量里 
	}
	if (dfn[x] == low[x])for (cnt++; st[top + 1] != x; top--)col[st[top]] = cnt, new_val[cnt] += val[st[top]];//找到这个连通分量的代表，划分 
	/*
	为什么要有low?
		因为我们最后要划分强连通分量（上面的操作），但不知道什么时候划分，所以添一个low。
		当dfn==low时就统计，这样不重不漏。
	*/
}
void topsort() {
	for (int i = 1; i <= cnt; i++)if (!du[i])q.push(i), f[i] = new_val[i], ans = max(ans, new_val[i]);
	while (!q.empty()) {
		int h = q.front();
		q.pop();
		for (int i = 0; i < new_g[h].size(); i++) {
			int t = new_g[h][i];
			f[t] = max(f[t], f[h] + new_val[t]);//缩点后无环，能直接统计 
			ans = max(ans, f[t]);
			if (!--du[t])q.push(t);
		}
	}
}
int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++)val[i] = read();
	for (int i = 1; i <= m; i++) {
		int u = read(), v = read();
		g[u].push_back(v);
	}
	for (int i = 1; i <= n; i++)if (!dfn[i])tarjan(i);//这个点仍不在任一个强连通分量里 
	/*
	目的：把每个点都放进一个强连通分量里，这样缩点完后就不存在环，就可以拓扑排序了
	所以流程就是：
	1.缩点,使整个图无环，方便后面拓扑排序  复杂度：O(n+m)
	2.拓扑排序找最大路径 复杂度：O(m)
	*/
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < g[i].size(); j++) {
			int t = g[i][j];
			if (col[i] != col[t])new_g[col[i]].push_back(col[t]), du[col[t]]++;//记录新图的边 
		}
	}
	topsort();
	cout << ans;
	return 0;
}