【BZOJ3160】万径人踪灭

fft劲啊

题目太长，拒绝帖原题

一句话题意：

给一个ab串，求不连续的回文子序列的个数

 

看zars19的题解（和代码）写出来的

恩，回文子序列满足个性质，假设s[i]==s[j]，他们的中点是mid

那么i+j==mid*2

卷积！

a设为1，b设为0自己卷一下，然后反过来b为1_a为0再卷一下

卷出来的a[i]表示以i为中心的最长回文子序列的长度

大概是酱紫：

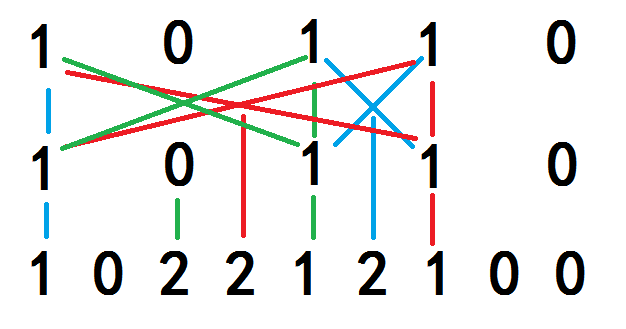
判重的话(a[i]+1)/2就可以辣

但是这题目要求是不连续的回文子序列，fft搞出来的会有连续的

所以马拉车搞一搞，减去连续的回文子串即可

原来fft要开4倍，因为卷积卷完后差不多会增长一倍……（比如乘法是吧，手玩一下

注意马拉车也要开两倍

数组没开够没有1A

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define ll long long
const int dalao=1000000007;
struct cp{
    double r,i;
    cp(double _r=0,double _i=0):  r(_r),i(_i){}
    cp operator+(cp x){return cp(r+x.r,i+x.i);}
    cp operator-(cp x){return cp(r-x.r,i-x.i);}
    cp operator*(cp x){return cp(r*x.r-i*x.i,r*x.i+i*x.r);}
};
char s[410000],ss[410000];  int n,nn;
cp a[410000],b[410000],tmp[410000];
int rvs[410000],dig[410000],N,L;
int f[410000];
void fft(cp x[],int mk){
    for(int i=0;i<N;++i)  tmp[i]=x[rvs[i]];
    for(int i=0;i<N;++i)  x[i]=tmp[i];
    cp _x,_y,wn,w;
    for(int i=2;i<=N;i<<=1){
        wn=cp(cos(2*M_PI/i),mk*sin(2*M_PI/i));
        for(int k=0;k<N;k+=i){
            w=cp(1,0);
            for(int j=k;j<k+i/2;++j){
                _x=x[j];  _y=x[j+i/2]*w;
                x[j]=_x+_y;  x[j+i/2]=_x-_y;
                w=w*wn;
            }
        }
    }
    if(mk==-1)  for(int i=0;i<N;++i)  x[i].r/=N;
}
ll mnch(){
    memset(f,0,sizeof(f));
    int mx=0,id=0;  ll bwl=0;
    for(int i=0;i<n;++i)  ss[i<<1]='#',ss[i<<1|1]=s[i];
    ss[nn-1]='#';
    for(int i=0;i<nn;++i){
        f[i]=(mx>i ? min(f[(id<<1)-i],mx-i) : 1);
        while(i>=f[i] && i+f[i]<nn && ss[i-f[i]]==ss[i+f[i]])  ++f[i];
        if(mx<f[i]+i-1)  mx=f[i]+i-1,id=i;
        bwl=(bwl+f[i]/2)%dalao;
    }
    return bwl;
}
ll qckpw(int x,int y){
    ll bs=x,bwl=1;
    while(y){  if(y&1)  bwl=(bwl*bs)%dalao;  bs=(bs*bs)%dalao;  y>>=1;}
    return bwl;
}
int main(){//freopen("ddd.in","r",stdin);
    //freopen("ddd.out","w",stdout);
    scanf("%s",s);  n=strlen(s),nn=n<<1|1;
    for(N=1,L=0;N<n;N<<=1,++L);  N<<=1,++L;
    for(int i=0;i<N;++i){
        int l=0;
        for(int j=i;j;j>>=1)  dig[l++]=j&1;
        for(int j=0;j<L;++j)  rvs[i]=(rvs[i]<<1)|dig[j];
    }
    for(int i=0;i<n;++i)  a[i]=cp(s[i]=='a'),b[i]=cp(s[i]=='b');
    for(int i=n;i<N;++i)  a[i]=b[i]=cp(0,0);
    fft(a,1),fft(b,1);
    for(int i=0;i<N;++i)  a[i]=a[i]*a[i],b[i]=b[i]*b[i];
    fft(a,-1),fft(b,-1);
    ll ans=0;  int tmp;
    for(int i=0;i<N;++i){
        tmp=((int)(a[i].r+b[i].r+0.5)+1)/2;
        ans=(ans+qckpw(2,tmp)-1)%dalao;
    }
    ans=(ans+dalao-mnch())%dalao;
    cout<<ans<<endl;
    return 0;
}