代码随想录第二十天 | Leecode 235. 二叉搜索树的最近公共祖先 、 701.二叉搜索树中的插入操作 、450.删除二叉搜索树中的节点

Leecode 235. 二叉搜索树的最近公共祖先

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

• 示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

• 示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

递归法，解题思路与代码

前两天刚做过一道求一般二叉树的最近公共祖先的题目，而本题在原本基础上新增了二叉搜索树的条件就变得简单了许多。只要从上往下遍历的时候找到一个节点处于两个目标数形成的左闭右闭区间中，那么该节点就是我们要找的最近公共祖先。那么可以写出如下代码：

class Solution {
public:
    TreeNode* findHelper(TreeNode* curNode, int minVal, int maxVal){
        if(curNode->val > maxVal) return findHelper(curNode->left, minVal, maxVal);  // 如果当前节点落在左闭右闭区间右侧，则在当前节点的左子树中找
        if(curNode->val < minVal) return findHelper(curNode->right, minVal, maxVal); // 如果当前节点在左闭右闭区间左侧，则在当前节点的右子树中找
        return curNode;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        int maxVal = max(p->val, q->val); // 分别记录p、q两个节点的最大值和最小值
        int minVal = min(p->val, q->val);
        return findHelper(root, minVal, maxVal); // 调用辅助函数递归查找
    }
};

同样也可以不使用辅助函数，直接用一个函数进行递归，

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        int maxVal = max(p->val, q->val); // 分别记录两个目标节点中的最大和最小值
        int minVal = min(p->val, q->val);
        if(root->val > maxVal) return lowestCommonAncestor(root->left,p, q); // 如果当前值更大，则递归前往左子树中查找
        if(root->val < minVal) return lowestCommonAncestor(root->right, p, q); // 如果当前值更小，则递归前往右子树中查找
        return root;
    }
};

上面算法的时间复杂度与空间复杂度都是\(O(h)\)，其中\(h\)表示树的深度。

Leecode 701. 二叉搜索树中的插入操作

题目描述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

• 示例 1：

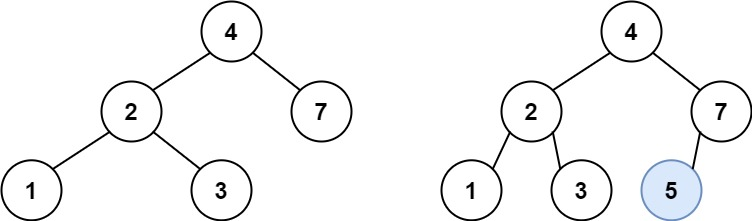
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

• 示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

• 示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

递归插入

本题只需要满足插入后仍然是一个二叉搜索树即可，那么我们可以考虑只在空位插入待插入的值，即根据二叉搜索树中的大小关系进行搜索，找到满足条件的空位那么就在此处插入一个节点。
可以写出代码如下：

class Solution {
public:
    void insertHelper(TreeNode*& root, int val){
        if(!root) { // 如果当前节点为空，说明找到一个可以插入的空位
            root = new TreeNode(val); // 则直接在此处新建一个节点插入待插入值
            return;
        }
        if(val > root->val) insertHelper(root->right, val); // 如果待插入值比当前节点值更大，则递归地去当前节点的右子树中找空位插入
        else insertHelper(root->left, val); // 如果待插入值比当前节点值更小，则递归地去当前节点的左子树中找空位插入
    }

    TreeNode* insertIntoBST(TreeNode* root, int val) {
        insertHelper(root, val); // 直接调用辅助函数进行递归插入
        return root; // 返回已经插入后的根节点
    }
};

Leecode 450. 删除二叉搜索树中的节点

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

• 示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
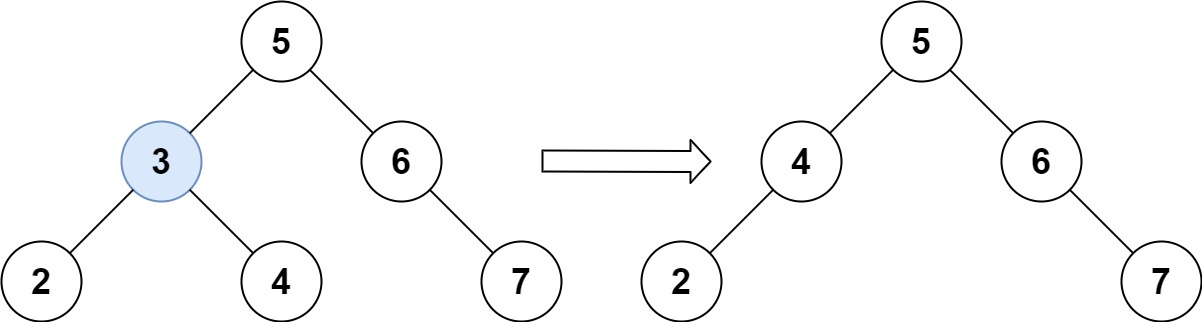
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

• 示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

• 示例 3:

输入: root = [], key = 0
输出: []

递归法-求解思路

使用递归来进行删除，首先需要找到待删除的节点，如果找不到则直接返回。当找到了再进行删除操作。查找的过程非常简单，如果当前值更大，则去其左子树中找；如果当前值更小，则去右子树中找。
随后删除的过程也需要进行分情况讨论：

• 如果待删除节点的左右子树至少有一个为空，那么就把另外一半子树的根节点嫁接替代当前节点，即可删除完毕。
• 如果两个节点都为空，与上面操作一致，直接把任意一个子节点（此时为空节点）用于替代当前节点，也算删除完毕。
• 如果要删除的节点的两个子节点都不为空，此时就是最麻烦的情况。此时待删除节点中的值需要用左子树中的最大值，或者是右子树中的最小值来进行替代。之后再递归删除被我们拿上来替代当前节点的那个节点即可。

根据上面思路，下面直接给出代码：

class Solution {
public:
    void deleteHelper(TreeNode*& curNode, int key){
        if(!curNode) return; // 如果一直找到叶节点以下（即当前节点为空），都还没有找到要删除的值，直接返回
        else if(curNode->val > key) deleteHelper(curNode->left, key); // 如果当前节点值更大，则去左子树里查找并删除
        else if(curNode->val < key) deleteHelper(curNode->right, key); // 当前节点值更小，则去右子节点里查找并删除
        else if(curNode->val == key){ // 如果当前节点就是要删除的节点，说明找到了待删除节点
            if(!curNode->left)curNode = curNode->right; // 如果当前节点的左右子树有一个为空，则直接将另外一颗子树嫁接过来即可
            else if(!curNode->right)curNode = curNode->left;
            else{ // 如果左右两个子树都不为空，则当前节点要变成左子树中最大节点，或是右子树中最小节点。这里使用左子树最大节点值
                TreeNode* maxLeftNode = curNode->left; // newNode用于记录左子树中的最大节点，先进入左子树中初始化
                while(maxLeftNode->right){ // 进入左子树之后一直往右走，即可找到最大的那个节点
                    maxLeftNode = maxLeftNode->right; 
                }
                curNode->val = maxLeftNode->val; // 将当前要删除的节点值用左子树中最大值替代
                deleteHelper(curNode->left, maxLeftNode->val); // 再删除左子树中的那个最大值节点
            }
        } 
        return;
    }

    TreeNode* deleteNode(TreeNode* root, int key) {
        deleteHelper(root, key);
        return root;
    }
};
    }
};

分析上面代码的时间与空间复杂度：

• 时间复杂度:\(O(h)\)，除了待删除节点有两个子树的情况之外，都只用从上往下进行搜索一次。而对于有两个子树的情况，找到待删除节点并找到左子树中最大值后进行替换的时间为\(O(h)\)，之后再去左子树中删除用于替换的那个节点所用时间还是\(O(h)\)。故总的时间复杂度为\(O(h)+O(h)=O(h)\).

• 空间复杂度: \(O(h)\)，来自于递归函数调用栈，最多需要调用的次数和深度有关.

今日总结

今天主要都是走到处理二叉搜索树，要说难度的话也就只有最后一道稍微难一些，前两道都感觉挺eazy的。另外最近感觉逐渐习惯每天刷题写博客的节奏了，刚开始那几天感觉非常麻烦幸好是一直坚持下来了，最近除了刷文档里的任务之外同时还会随机在力扣上多刷几道。希望之后再接再厉，早日刷完200题。

今天刷到第75题了，继续加油！