单变量微积分学习笔记：函数的导数（3）【1】

导数的定义

\[f'(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \]

\[f'(x) = \lim_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0} \]

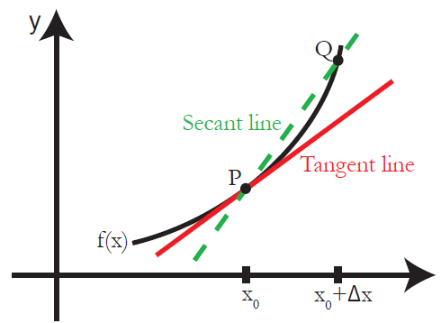
割线（Secant line）：经过函数图像任意两个不重复的点的直线

切线（Tangent line）：两点无限接近的割线，切线的斜率（slope）被称为导数（Derivative）。

1. 牛顿记法：Newton’s Notations
   \(f'\)

2. 莱布尼茨记法：Leibniz’s Notations
   \(\frac{df}{dx} = \frac{dy}{dx} = \frac{d}{dx}f = \frac{d}{dx}y\)

可导的条件

\[\lim_{x \to x_0^+} \frac{f(x) - f(x_0^+)}{x-x_0^+} = \lim_{x \to x_0^-} \frac{f(x) - f(x_0^-)}{x-x_0^-} \]

\(|x|\)在\(0\)处不可导：

\(\lim_{x \to 0^+} \frac{f(x) - f(0^+)}{x-0^+} = 1\)

\(\lim_{x \to 0^-} \frac{f(x) - f(0^-)}{x-0^-} = -1\)