IOI2021 国家集训队作业总结&部分题解
前言
(写题解鸽了)
下文中会对作业的每道题目做个人评价。尽量客观,但难免有主观意愿,如有异议可友好讨论。
评价的符号表达:
E 表示不在作业中或质量较低的题目,一般只有很无聊的模拟或阅读或板子会质量较低,这部分题目一定不会写题解;
H 表示质量中等的题目,一般是知识不难、算法思考的弯路较少、坑点也很少的题,这部分一些有点意思的可能会写题解;
C 表示较高质量的题目,算法难度(包括证明)、代码难度、大坑点、命题创意都可以体现高质量,大部分会写题解。
G 表示质量极高的题目,一般是我被坑了很久或者卡了很久或者完全不会(可能现在都不怎么会)或者印象特别深刻的题目,这部分一定会写题解。
Easy Hard Chaos Glitch
因为是集训队作业所以质量大部分和难度相关,但很有趣的清新题的质量也会标的比较高。
更新日志
2020.11.24:DJ,ED,MB,SI,UI
2020.11.20:加了 EI 的 BB 证明;EC,EJ,LD,LE
2020.11.16:BB,CJ,DA,DH,ME
2020.11.13:FC,FF,KE,JG
2020.11.12:AJ,AL,BK,CH,HI,KD,TE
A.WF2014
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | C | C | H | E | C | H | C | C | C | G | H | G |
***J. Skiing
按照 \(y\) 坐标从小到大排序。有一个显然的 dp:设 \(f_{i,j}\) 表示从 \(i\) 开始以初速度为 \(j\) 滑最多能滑多少个点。但是其状态肉眼可见的多。
注意到对于 \(f_{i,j}\) 中相邻且值相等的 \(j\) 可以合并成一个区间一起转移。故可以将 \(f_i\) 的所有状态看成若干个三元组 \((l,r,t)\) 表示速度在 \([l,r]\) 内答案为 \(t\)。有一个结论是对于确定的 \(i\),\(f_i\) 构成的三元组个数是 \(O(n)\) 的,但我找了 wyp 和 slz,后面又通过玄秘方式找了 WF2014 的直播和 bmerry 的博客,都没有找到这个结论的证明。希望有神仙来教育教育我 TAT。
这样我们就可以从 \(f_{i+1 \sim n}\) 的 \(n^2\) 个区间进行转移了,转移过来的速度区间可以通过解一元二次方程得到,需要注意加速度为 \(0\) 时这个方程的二次项系数是 \(0\)。同时还要注意重点的转移。合并的时候要排序,所以复杂度是 \(O(n^3 log n)\)。因为直接写 set 区间覆盖太不优美了,所以这里参考了别人的实现,实现方式是按照经过点数为第一关键字区间左端点为第二关键字排序然后依次合并,并没有把相同速度的值更小的状态给删掉。
最后输出方案。需要注意的是找到了重要点序列的下一个位置之后,有可能有若干个速度区间是合法的,由于后面的决策和每个速度区间都有关,所以需要维护可行的所有速度区间。
*L. Wire Crossing
WC2013 平面图弱化版???
将线段的两两交点拿出来,如果两个交点是某条线段上的所有交点中直接相邻的,则在它们之间连一条线段。这样可以得到一张平面图。需要求的是两个面之间的任意折线最少经过多少次线段,实际上就是对偶图上两个面的最短路。
建立对偶图可以沿着 \(x\) 轴扫描线,用 set 维护穿过当前扫描线的所有线段的从下往上的顺序以及两条相邻的线段之间的面对应在对偶图上的点的编号,有新的点加入时进行更新。扫到起始和目标点的时候进行询问。
最后跑一次 bfs 即可。复杂度 \(O(n^2 \log n)\)。
坑点:
- 记得随机转角避免平行坐标轴的直线(当然如果这东西判起来不麻烦的话也可以直接写)
- 在加删线段的时候 set 中使用的 compare 应该是这两条线段对应的横坐标区间的交上任意一个非端点上两条线段对应点的取值的大小关系。之前好像写成了右端点纵坐标的大小关系 = =。
B.WF2015
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | G | E | E | C | E | C | C | E | H | G | C | E |
**B.Asteroids
首先可以把速度合成一下使得只有第一个多边形在动。
判断 never 可以分别对两个凸包的顶点计算第一次与另一个凸包接触的时间,如果全都是 INF 就是无解。
然后有两个做法:
做法 1
把两个凸包三角剖分然后维护两两之间交面积的函数然后求和维护最大值。这个交面积函数会是 \(O(1)\) 段不超过二次的分段函数,可以插值插出。
做法 2
- 结论:交面积关于时间的函数是一个单峰函数,证明可参考 EI 博客
这样可以三分然后半平面交算面积。这个需要特殊判断交面积为 0 的情况因为接触和无交都会把面积算成 0。
**K. Tours
结论还是很简单的:将桥边去掉之后拿出所有的环,对每条边记录包含它的环集合,将所有边分为环集合的等价类,那么答案就是所有的等价类大小的 \(\gcd\) 的所有约数。
证明难度比较大。可参考 orz yhx。
具体实现时根据众所周知的“拿出图的一棵 dfs 树,其中一条非树边和其两端点的树上路径所构成的环是这个图的环空间的基”的结论,我们只需要考虑所有只经过一条非树边的环。对于一个环,对环上所有边的边权异或上一个 unsigned long long 范围的随机整数,初始所有边边权为 0,这样最后得到的边权等价类有极大概率就是环覆盖的等价类,具体而言对于两条边有 \(\frac{1}{2^{64}}\) 的概率将不在同一个等价类判做在同一个等价类。
C.WF2016
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | H | C | E | E | E | C | E | G | C | G | H | E | E |
*H. Polygonal Puzzle
基本思路是很简单的:枚举两条边,通过旋转让它们与 \(x\) 轴平行,通过纵坐标平移让这两条边的纵坐标相同。然后从负无穷远处不断将第一个多边形平行于 \(x\) 轴进行平移并维护交线长度和是否重合,注意这里的重合是指有非 0 的交面积,然后计算其中的最大值。
然后就有很多实现上的注意点了。
-
枚举了两条边之后通过旋转让它们平行实际上有两种方式,将一个方式中的其中一个多边形旋转 \(180^\circ\) 之后可以得到另一个方式。
-
判断是否重合这个问题不是很好处理,我使用的是闵可夫斯基差(就是把 \(a+b\) 变成了 \(a+(-b)\) 和闵可夫斯基和是一个东西)。具体来说先对两个多边形三角剖分,然后两两枚举三角形,考察它们的闵可夫斯基差中 \(y=0\) 的所有点构成的横坐标区间,那么对于这段区间中的任一非端点位置,两个多边形是重合的。
-
对非凸多边形进行三角剖分,可以直接每次枚举边上三个相邻的点,考察它们所构成的三角形是否完全落在多边形内,这里我的判断方法是是否存在一条多边形上的边与三角形有非平凡交点以及判断三个点之间的位置关系。
-
对于计算交线直接枚举两条多边形上的线,对于与 \(x\) 轴平行的两条线,交线长度与平移位置的关系是一个分段的不超过 1 次的函数,可以通过差分维护;对于不平行于 \(x\) 轴的两条线,如果它们平行那么就是在一个确定的平移位置上答案增加了一个值。
-
最后将所有分段函数的变化点、不平行于 \(x\) 轴的线的相交点和是否重合的变化点拿出来扫描一次就可以了。一定要注意判断重合的区间是开区间。
*J.Spin Doctor
特判只有一个 \(c=1\),然后对 \(c=1\) 的点建凸包,判掉这些点落在同一直线上的情况。那么现在的问题是求最优的直线斜率满足凸包的这个斜率的两条切线之间点数尽可能少。先把凸包内部 \(c=0\) 的点加进答案。
考虑凸包外的一个点计算其在怎样的斜率范围内会产生贡献。先计算出经过这个点的凸包的两条切线和在与 \(y\) 轴平行的直线上这个点是否在两条切线内。那么考虑直线斜率从 \(\infty\) 变小到 \(-\infty\) 的过程中,如果直线斜率变化到这两个斜率中的某一个时,这个点是否在切线之间的状态就会发生翻转。
那么将每一个点贡献的变化点拿出来排序扫一遍即可。注意在斜率相等的情况下要先加后减,为了避免精度误差可以用向量方向代替直线斜率,同时还要注意一条切线恰好与 \(y\) 轴平行的情况。
计算经过一凸包外的点 \(A\) 的凸包的两条切线感觉我的做法比较生硬:考虑任一与凸包交非空的经过 \(A\) 的直线,先判掉其恰好是一条切线的情况,对于其他情况在凸包上二分出这条直线左边和右边的部分,然后分别在两个部分二分出一条切线。似乎直接在凸包上二分会出现一些我不会处理的问题。
D.WF2017
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | G | H | E | C | E | E | C | G | E | G | G | C |
*A. Airport Construction
首先一个容易发现(猜出)的结论是最长的线段一定会经过至少两个多边形的顶点,这很容易通过移动和旋转的方式证明。因此枚举两个顶点,计算经过这两个顶点的线段的最长长度。
首先判掉两点的连线完全落在多边形外的情况。
枚举每条边,算出当前直线与这条边的严格交点(严格交点要求不是该边的端点)。如果交点存在且唯一且在该两顶点之间那么就不存在经过这两个顶点的线段;否则这个顶点的影响是对其中一个顶点的延伸方向有限制。记录下两边的最紧限制。
为什么一定要求严格交点且交点唯一?原因是如果非严格交点恰好是一个端点,而这个端点的两条邻边恰好在直线两侧,这个端点实际上不会产生影响。对于两线重合的情况也是类似的。因此需要单独判断直线穿过某个顶点和与某条边重合的情况。
需要注意的是当前直线与某条边重合,而其旁边两条边分属两侧时,根据当前直线在这条边的左边还是右边,它的限制是不同的;同时如果当前直线与某条边重合,而其旁边两条边分属同侧时,根据在这个图形的内侧还是外侧也是有影响的。这个我之前一直没有意识到,对应的就是下图的情况。
最后点的范围是 \(10^6\) 因此最劣情况交点之间的坐标差在 \(10^{-12}\) 范围,eps 要开到这个范围才行。
**H. Scenery
以下除了最后两段不一样以外都是 solution 翻译(
一个显然的贪心是靠左放,每次选右端点最小的删掉,但样例 3 就会锅,原因是放 \([5,15)\) 之后 \([10,20)\) 立即不合法,但放在 \([20,30)\) 却合法。
虽然朴素贪心是错的,但这也给了启发。\([10,20)\) 这样的区间不仅对 \([10,20)\) 这段区间有限制不能开始拍照,对于 \((0,10)\) 也不能开拍,否则就和 \([10,20)\) 撞了。这意味着在贪心之外有其他限制。
考虑任一区间 \([l,r]\) 并拿出满足 \(l \leq l' \leq r' \leq r\) 的所有输入区间 \([l',r']\),并忽略其原本限制,只要求其在 \([l,r]\) 内拍,要求最早拍的时间尽可能晚。这显然可以得到从右往左放的贪心。
设最早拍时间是 \(t\),如果 \(t<l\) 那么直接挂掉,若 \(l \leq t < l + k\),此时由于这一段区间的开始时间至多是 \(t\),那么其之前的最后一次拍摄不能在 \(t-k\) 时刻之后开始,即 \((t-k,t)\) 是被限制的,否则就撞上了。对于其他的情况由所有已知条件还暂时找不到显然的限制。
可以得到若干限制区间,同时在上文的贪心过程中也把之前找到的限制区间考虑进去让限制更紧。为了保证不出现某个区间处理完之后在中间又出现新的限制区间的情况,按照 \(l\) 从大到小的顺序依次处理。
有用的 \(l,r\) 只有 \(n\) 种,同时由于所有的限制都是某一个左端点向前若干长度,对于每个左端点可以合并其所有限制,所以限制只有 \(n\) 种。暴力是 \(O(n^3)\) 的,优化到 \(O(n^2)\) 考虑将左端点向前移动后每个右端点答案的影响,就是对于 \(O(n)\) 个右端点需要再放一个区间。用一个指针维护当前位置之前的第一个限制然后不断往前扫,这样就可以 \(O(n^2)\) 地得到在这样的条件下是否合法。
这很显然是一个必要条件,接下来将会证明满足这样的输入可以得到一个合法解,其中合法解是在考虑给出的这些限制的情况下按照开头的显然贪心进行选择得到的方案。首先如果这个方案合法那么得到了答案,那么只需要说明不合法的情况一定会被上文的判断给判掉。
首先对于从前往后贪心没有选到的位置,我们可以认为其是被额外限制的。如果某个被额外限制的时刻可以拍摄而不碰到被限制的区间,那么这个时刻就是无照可拍的。对于一个无照可拍的时间 \(X\),其之前和之后可以分开考虑。故后文中仅考虑不存在无照可拍的时间 \(X\) 的情况。
考虑按照贪心顺序给输入区间编号为 \((s_1,e_1),\ldots,(s_n,e_n)\),且仅有第 \(n\) 个区间的结束时间超过了它的 DDL。由于其中不存在无照可拍的时间,所以其贪心放置的策略就是从 \(s_1\) 开始从左往右尽可能靠前放第一个可以拍照的位置,不需要考虑每个区间开始时间的限制。
如果 \(e_n\) 是所有 \(e_i\) 中非严格最大的,那么考虑 \((s_1,e_n)\) 区间从右往左贪心靠后放也不会合法,这已经判断过了。
如果存在 \(e_j > e_n\),找到其中最大的 \(j\),设其在 \([v_j,v_j+k)\) 拍,设 \(s = \min_{i=j+1}^n s_i\)。由于 \(\forall p\in[j+1,n] , e_p \leq e_n < e_j\),所以当第 \(j\) 个区间放入的时候,\(j+1 \sim n\) 这些区间一定都由于开始时间限制无法放入,即 \(v_j < s\)。考虑区间 \((s,e_n)\) 是否合法,如果其不合法显然已经判断过了,否则由于 \(j\) 能影响 \((s,e_n)\) 使其不合法,这意味着 \([v_j,v_j+k)\) 必定覆盖 \((s,e_n)\) 方案中最早的拍摄时间 \(t\),即 \(v_j > t - k\)。而 \(v_j < s\),这意味着 \(v_j\) 落在了 \((s,e_n)\) 产生的限制区间里,也就是说第 \(j\) 个区间当前的拍摄位置是被限制的位置,与贪心策略不符。
所以如果满足判断的条件,总能构造出合法方案。复杂度 \(O(n^2)\)。
**J. Son of Pipe Stream
首先 \(v\) 是没用的,可以除掉最后再把它乘上去。很显然能够看出来这个问题是一个网络流问题,\(F\) 和 \(W\) 指的就是 \(1,2\) 到 \(3\) 的流量。
最开始我写了一个垃圾做法:可以通过退流的方式说明 \(W\) 关于 \(F\) 是上凸函数。同时由于 \(F+W\) 确定时,不妨设其为 \(V\),则 \(F^\alpha (V-F)^{1 - \alpha}\) 也是上凸函数,这可以用求导、作比等方式简单证明。所以答案关于 \(F\) 也是一个上凸函数,三分即可。复杂度 \(O(flow * \log \frac{1}{\epsilon})\)。
但上面的算法忽略了 \(W\) 关于 \(F\) 的函数的优美性质:设 \(1\) 到 \(3\) 的最大流是 \(F_{\max}\),\(2\) 到 \(3\) 的最大流是 \(W_{max}\),\(1,2\) 到 \(3\) 的最大流是 \(V\),那么 \(W = \min(W_{\max} , V - F_{\max})\)。
那么有意义的段实际上只有 \(F \in [V - W_{\max} , F_{\max}] , W = V - F\) 这一段。上面也提到了在这一段上 \(F^\alpha (V-F)^{1 - \alpha}\) 是上凸的,更具体的其最大值点在 \(\alpha * V\) 处取到,所以在这段区间上的最大值点是容易得到的。最后再跑一次浮点数网络流构造方案,复杂度 \(O(flow)\)。
E.WF2018
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | G | C | H | E | C | H | H | G | E |
**C. Conqure the World
两个做法:
做法一
考虑 dp: 设 \(f_{i,j}\) 表示考虑点 \(i\) 的子树,\(j\geq0\) 表示还有 \(j\) 个军队要求匹配但没有匹配,\(j<0\) 表示还有 \(-j\) 个需求没有满足,这样的最小代价。直接暴力复杂度不正确。为了描述方便,这里的代价增加了这 \(|j|\) 个物品到达 \(i\) 号节点的代价总和。
由于这题的费用流模型非常显然,所以考虑与费用流息息相关的凸性性质上。实际上我们有性质:
- \(f_i\) 是下凸的,即若 \(f_{i,j-1},f_{i,j+1}\) 均有意义,那么 \(f_{i,j}-f_{i,j-1} \leq f_{i,j+1}-f_{i,j}\)。
证明. 设 \(S_x\) 为 \(i\) 子树的 \(x\) 和,\(S_y\) 为 \(i\) 子树的 \(y\) 和,那么 \(f_{i,-S_y}\) 是已知的。考虑这样的一个费用流:仅考虑 \(i\) 子树中的点,对于每个点 \(u\),从源点向其连流量 \(x_u\) 费用为 \(0\) 的边,向汇点连流量 \(y_u\) 费用为 \(-dist(u,i)\) 的边,费用表示一个需求满足了,那么它就不需要跑到 \(i\) 了。树上的一条边 \((i,j,c)\) 连双向的流量 \(+\infty\) 边权为 \(c\) 的边。对于 \(i\) 号点,特别地连一条向汇点流量 \(+\infty\) 费用为 \(0\) 的边,用来容纳 \(j\) 为正的时候的剩余流量。对其运行最小费用流,由于选择 \(i\) 号点流量 \(+\infty\) 的边总不如选择匹配需求的边优,所以当流量 \(F\) 不超过 \(S_y\) 时,其表示的就是匹配了 \(F\) 组的情况下匹配代价加上剩余所有需求与 \(i\) 的距离和的最小值,大于 \(S_y\) 时其表示的就是全部匹配完之后匹配代价和多出来的军队与 \(i\) 的距离和的最小值,正是 \(f_{i,F-S_y}\) 的定义。由最小费用流的性质,费用与流量的关系是一个下凸函数,这样 \(f_i\) 也是一个下凸函数。
这样 \(f\) 是凸函数,考虑用平衡树维护将 \(f\) 差分之后的结果记做 \(\Delta f\),然后考虑转移:
- 将一个儿子合并上来的时候,有转移 \(f'_{i,j} = \min(f_{i,k} + f_{son,j-k})\)。
这是下凸函数的 \(\min\) 卷积。设 \(f'_i\) 中有意义的最小下标为 \(L\),那么计算 \(f'_{i,L+k}\) 是从 \(\Delta f_i\) 和 \(\Delta f_{son}\) 中分别选出一个前缀满足数量和为 \(k\) 且和尽可能小。由于 \(\Delta f\) 单调不增所以可以将问题进行松弛为从 \(\Delta f_i\) 和 \(\Delta f_{son}\) 中选出总共 \(k\) 个数使得和尽可能小。由于 \(\Delta f\) 单调不增所以这样选总是会选出两段前缀。松弛之后问题是简单的,只需要贪心选最小的就行了,而两个数组已经有序,所以只需要将它们归并起来就可以得到 \(\Delta f'\) 了。用 finger search 实现启发式合并,复杂度 \(O(S \log S)\),其中 \(S\) 为出现在平衡树中的点数总和。实现 finger search 可以直接使用 splay。
- 在当前点加入一些需求或者加入一些军队
由于需求一定要满足,所以加入一个需求后 \(f'_{i,j} = f_{i,j+1}\),直接修改有意义的最小下标即可。
而军队不一定总是要选,所以加入一个军队有 \(f'_{i,j} = \min(f_{i,j} , f_{i,j-1})\),对于 \(\Delta f\) 小于 \(0\) 的位置会选择从当前位置转移;对于 \(\Delta f\) 大于等于 \(0\) 的位置会选择从前面转移。这种转移在 \(\Delta f\) 上体现为插入一个 \(0\) 并保证 \(\Delta f\) 的有序。
- 将一个点的信息往上合并的时候还要更新 \(f'_{i,j} = f_{i,j} + |j| dist_{j,fa_j}\)。
直接考虑 \(\Delta f\) 产生的变化。对于 \(\leq 0\) 的位置 \(\Delta f\) 减小了 \(dist_{j,fa_j}\),其他位置增大了 \(dist_{j,fa_j}\)。通过最小有意义位置二分出 \(\leq 0\) 和 \(>0\) 的部分并分别打上标记即可。
可以发现只有 2 情况加入军队的时候会插入节点,如果一个个插入总复杂度是 \(O(\sum x \log \sum x)\),但实际上可以把它们当成一个节点插进去,在需要分裂开的时候再分开,复杂度就是 \(O(n \log n)\) 的。
做法二
WC2019 上 laofu 讲了一个叫老鼠进洞的模型。我们直接把它搬到树上。
维护两个堆,分别表示可以匹配的老鼠(军队)和可以匹配的洞(需求)。为了匹配方便我们认为落在 \(i\) 点的一个物品的权值加上 \(dist_{1,i}\),当位于 \(i,j\) 的两个物品在 \(LCA_{i,j}\) 处匹配的时候权值减去 \(2dist_{1 , LCA_{i,j}}\)。为了方便对于一个老鼠,可以先认为其与一个代价为 \(+\infty\) 的洞匹配,并在后面进行反悔;也就是答案加上 \(+\infty\),匹配这只老鼠的代价减去 \(\infty\)。
从下往上计算,计算到一个点的时候先把所有儿子的老鼠和洞的堆合并起来, 把自己的老鼠和洞放进去。然后每一次找两个堆的堆顶,如果它们的匹配代价 \(<0\) 就进行一次匹配;但这样匹配有可能在上面还会不优,也就是可能会反悔,所以还要往老鼠和洞的堆里面丢一个将这个匹配撤销掉的元素,也就是原来它们的权值减去匹配代价作为新的权值的元素,以完成反悔。
注意到一次匹配会往老鼠和洞的堆里面都丢一个反悔,但如果它们都反悔了的话这两个匹配中就会有至少一条边重合,所以是不优的。所以就算丢了两个也至多只有一个会被拿出来匹配。(好像这样不太严谨……)
这样的话每匹配一次就会有两个可以用于反悔的元素拿出来,然后丢一个用于反悔的元素进去。由于初始元素是 \(O(\sum x)\) 的,所以总匹配次数也是这个级别的。使用可并堆,复杂度 \(O(\sum x \log \sum x)\)。
D. Gem Island
***J. Uncrossed Knights Tour
大概是先用插头 DP 算比较小的 \(n\) 的答案,然后观察一下对于每一个 \(m\),当 \(n\) 足够大的时候总存在两个数 \(l_m,v_m\) 满足 \(ans_{m,n} = ans_{m,n-l_m}+v_m\)……
插头 DP 是不可能写的所以这个题鸽了
F.WF2019
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | H | G | E | E | G | H | E | C | H | C |
***C. Checks Post Facto
没写过这个题,口胡一下实现(口胡一时爽码题火葬场),如果有锅请用力喷。
对于当前的棋盘,记录以下信息:每个位置是否已知其状态(这个状态指的是空格/黑棋/白棋)、如果是棋子是否已知其是否是皇后,然后一次移动可以知道一些形如当前状态某个格子是某种颜色的某种棋子的信息,更新一下。值得注意的是一次移动可以得出所有棋子都不能跳跃,从而得到一系列格子是空格;一次跳跃的结束也可以知道类似信息。最后未知状态的棋子是普通棋子一定更优,对于未知状态的格子是空格一定更优,这样更容易满足能跳必跳的策略。
*F. Directing Rainfall
考虑自上而下扫描线并维护对于每个 \(x\) 坐标从起点让雨滴落在当前扫描线的这个位置需要的最小代价。考虑新扫到一条雨棚的影响,如果这条雨棚斜率为正,则是这一段区间拉出来做一个后缀 \(\min\) 然后对于非左端点位置区间 \(+1\);如果这条雨棚斜率为负则是这段区间拉出来做一个前缀 \(\min\) 再对于非右端点位置区间 \(+1\)。
先考虑加入雨棚的顺序。注意这里并不能简单的按照端点坐标进行排序,而是应该按照直线的位置关系进行排序,也就是从高到低依次加入。这里可以先从左往右做一个扫描线算一下雨棚之间的拓扑关系,再拓扑排序计算一个合法的加入顺序。
然后考虑上面的操作如何去做。对原序列进行差分,区间前缀 \(\min\) 就是将除了左端点之外的所有差分值拿出来,对于差分值为正的做一次推平,后缀 \(\min\) 就是除右端点之外做差分值为负值的推平。将差分值为 \(0\) 的一段缩起来可以保证一次推平可以至少减少一段,而其他操作的增加段数是线性的,所以这里的复杂度就是 \(O(n \log n)\) 的。具体维护的时候可以拿一个 set 维护分段,再拿两个 set 维护差分值为正和负的所有位置。注意是对于 \(x\) 坐标的答案维护只需要维护所有整点和两个相邻整点之间的某一个点的答案,因为有类似 \([1,3]\) 和 \([4,6]\) 有雨棚然后从 \(3.5\) 滴下去更优的情况。
总复杂度 \(O(n \log n)\)
G.NEERC17
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | E | E | E | C | H | G | C | C | C | H |
H.NEERC16
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | C | H | C | E | E | G | E | G | E | C | H | C |
I. Indiana Jones and the Uniform Cave
抽象一下问题,等于每一个点可以有两个状态 left,right 并可以标记一条出边,需要在规定步数内访问所有边。
算法流程是在整个图上 dfs 并维护其一棵 dfs 树,right 状态表示该点在 dfs 栈中,left 状态表示该点已经找完所有出边并回溯。对于 right 点,标记的边表示其在 dfs 树上指向儿子的边,left 点标记的出边选择见下文。同时在外部维护每个点在 dfs 树上的深度和已访问的边的数量。
对于栈顶点,如果其已经找完所有出边,则回溯,考虑标记哪条边。考虑所有出边,如果某条出边指向 right 点,则该边权值为其深度,否则权值为不断沿着标记的边走直到一个 right 点,这个 right 点的深度。从中选出权值最小的边,让这个回溯的点标记这条边,然后将该点标记为 left。然后不断沿着标记的边走直到到达一个 right 点,再通过不断走树边走到回溯后的栈顶。可以用反证法证明在这样的选择下,每次到达一个 left 点时总能通过不断沿着标记边走到达一个 right 点。
如果仍有出边未找到,则沿着其顺时针方向第一条边出去同时标记这条边。如果新的点状态是 center,则在栈中压入新点;如果是 left,则先不断走 left 再不断走 right,并数一下 right 点走了几个,以计算深度,更新该点的回溯出边;对于 right 点,可以先不断将树上从该祖先到该点的路径标记成 left 并沿着树边走直到第一次走到一个 left 点,这样就得到深度了,然后把所有栈中节点的 left 修改复原即可。
这样就可以沿着 dfs 的顺序访问所有边了,总步数是 \(O(n^2m)\) 的。
I.NEERC15
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | H | H | C | E | E | E | C | C | C | H | H |
J.NEERC14
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | H | C | C | E | G | C | C | E | E |
G. Gomoku
分析一下黑色的策略,可以简化为:设黑色下一步可以凑出的最长的活棋长度为 \(B\),白色已存在的最长活棋长度为 \(W\),若 \(B>W\) 则下自己的最长的棋,否则堵对手的 \(W\) 棋。
基本策略是造活三,因为首先同时出现两个活三可以直接定胜局,再者造一个活三之后如果对手造不出四子连棋,则一定会用两次来堵新造出来的活三,这样你可以再在旁边下两步,再造一个活三。
手玩了一下根据黑色第二步策略不同对应两个分支,横向翻转一下可以得到所有的四种情况。
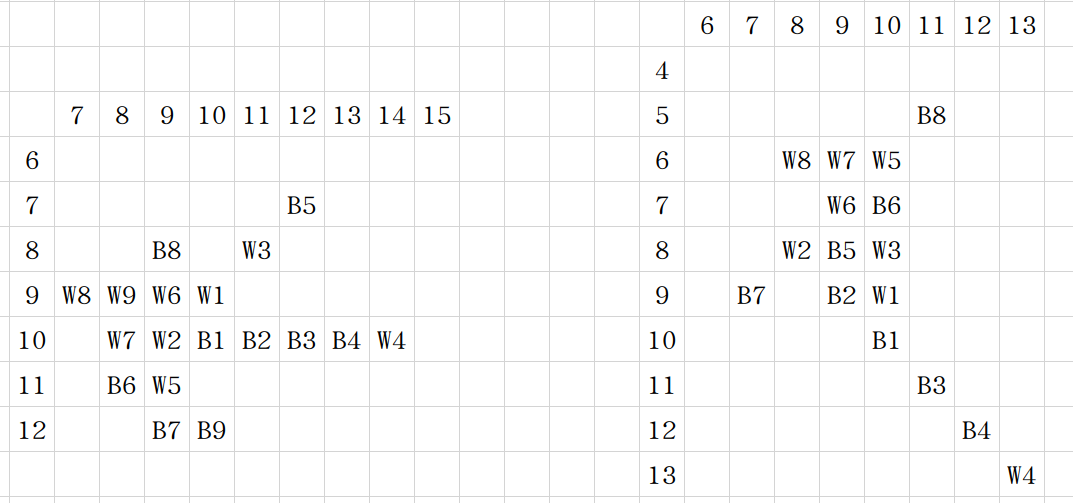
稍微需要注意的是两个情况的 \(B3,B4\) 都有可能不下在图上的位置,因为将 \(B3\) 下在 \(B3,B4,W4\) 位置实际上分数差别不大。所以这里堵的时候稍微注意一下,同时对于第二种情况,如果出现了 \(B3,B4\) 下在 \(B4,W4\) 的情况,还需要在右下角堵一下新的 \(B3,B4\) 再接一次造出来的三子连棋。
似乎还有确定解,不知道是怎么做到第一步不产生分支的 = =
K.NEERC13
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | C | G | G | E | C | H | H | E | H |
D. Dictionary
建立一张图,第 \(i\) 个字符串 \(s_i\) 对应点 \(i\)。设 \(p(i,j)\) 表示 \(s_i\) 的是 \(s_j\) 的子串的最长前缀长度。
对于一个字典,找到每个字符串在其上的任一匹配位置,并认为这个字符串覆盖了其匹配的所有树边。
考虑如下若干事实:
-
最优字典中一定不存在任一边不被任一字符串覆盖,否则删掉更优。
-
对于一个字典,将字符串按照匹配位置最浅点的深度从深往浅依次考虑。考虑到 \(s_i\) 时,找到最长的前缀长度 \(l\) 满足其结束位置对应的树边有其他字符串覆盖,由于其是匹配起始位置最深的点,因此总是存在另一个字符串 \(j\) 覆盖了 \(s_i\) 的长度为 \(l\) 的前缀。此时在图上从 \(i\) 向 \(j\) 连接一条长度为 \(l\) 的有向边,则显然 \(l \leq p(i,j)\)。那么字典可以表示成内向树,而字典节点数就是字符串总长减去所有边的边权和+1。
-
考察任一内向树,满足其中一条有向边 \((x,y,v)\) 有 \(v \leq p(x,y)\),则容易按照拓扑序通过该内向树构建一个合法的字典,方式和将字典转为内向树类似。
通过上面事实我们可以将“最小化字典树上节点数”转为“最大化内向树边权和”。在这个问题中,一条边 \((i,j,v)\) 的权值显然满足 \(v=p(i,j)\),故认为 \((i,j)\) 边权为 \(p(i,j)\) 通过朱刘算法计算出最大树形图并按照拓扑序构造方案即可。不考虑计算边权,复杂度 \(O(n^3)\)。
***E. Easy Geometry
有两个做法。
做法一
考虑有哪些可能的合法矩形。如果一个矩形不存在任意一对对角顶点同时卡在凸包的边上,则肯定可以让长或宽的其中一个增大。而存在一对对角顶点在凸包的边上则可以进行平移,使得最后只有这两种情况:
- 矩形的一对对角顶点卡在凸包上,且其中一个是凸包的顶点;
- 存在三个顶点卡在凸包上。
对于第一种情况可以枚举一个顶点,扫描线预处理其对角顶点在凸包上的合法范围,先二分出最优线段再 \(O(1)\) 得到这个线段上的最优点。
对于第二种情况,枚举矩形的哪一条平行于 \(y\) 轴的边卡在凸包上,不妨假设是靠左的边。对左凸壳从左往右扫描线,扫描的时候记录交点所在的线段和过两个交点做平行于 \(x\) 轴的直线与右凸壳的交点所在的线段,这显然只有 \(O(n)\) 个状态。对于每一个状态答案是两个二次函数的 \(\min\) 的形式,容易 \(O(1)\) 计算答案。
但是这个做法不那么好写,如果有更好的做法欢迎吊打我。QAQ
做法二
考虑如下性质:
- 设 \(f(w)\) 表示宽度为 \(w\) 的矩形的最大面积,则 \(f(w)\) 是单峰函数。
这玩意我不会证,有人会了可以教教我 TAT。
这样可以三分了,只需要计算 \(h_w\) 表示宽度为 \(w\) 时的最大长度就行了。
- 设 \(f_w(x)\) 表示以 \(x\) 为左边界横坐标、\(x+w\) 为右边界横坐标的矩形的最大长度,则 \(f_w(x)\) 是单峰函数。
可能正确的证明:\(f_w(x)\) 相当于将右凸壳向左平移 \(w\) 单位长度之后再做半平面交得到的多边形中横坐标相同的一对点的最大纵坐标差。新的图形也是凸壳,所以上端顶点纵坐标是对横坐标的上凸函数,下端顶点纵坐标是对横坐标的下凸函数,相减可知 \(f_w(x)\) 是凸的。
这样里面套一个三分,就只需要计算凸壳上横坐标为某个值的两点纵坐标,在凸壳上二分即可。复杂度 \(O(n + \log^2 \frac{1}{\epsilon} \log n)\)
L.CERC17
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | C | C | G | G | E | E | E | C | E | C | H |
**D. Donut Drone
拿 LCT 维护环套树实在是个垃圾做法(
由于 \(q,h,w\) 都比较小,可以考虑维护 \(nxt_i\) 表示从第 \(i\) 行开头走 \(w\) 步会走到哪一行开头,然后一次移动就从当前节点开始走到第一列然后再沿着 \(nxt\) 跑,循环节缩一下就可以了。
考虑修改元素之后怎么维护 \(nxt\)。有性质:
- 对于 \(1 \leq p < q \leq w\),\(r \in [1,h]\),从第 \(p\) 列出发走 \(q-p\) 步到达第 \(q\) 列时恰好到达第 \(r\) 行的行编号构成一段区间。注意这里的区间是 \(1 \sim n\) 构成的环上的一个区间。
证明. 如果从第 \(p\) 列第 \(x,y\) 行开始走,到达第 \(q\) 列时都恰好到达第 \(r\) 行,且从第 \(x\) 行开始的路径在从第 \(y\) 行开始的路径的上方。这里上方的定义是从 \(q\) 往 \(p\) 考虑两条路径的第一次分岔,分岔靠上的整条路径就是靠上的。而在区间 \([x,y]\) 中存在一个 \(z\) 满足到达第 \(q\) 列时不落在第 \(r\) 行,此时\((z,p) \rightarrow (arrive_z,q)\) 与 \((x,p) \rightarrow (r,q),(y,p) \rightarrow (r,q)\) 这两条路径至少有一条相交,而两条路径相交时一定会出现两个格子选择了不同的下一步,而它们的下一步都是这两个格子可行的下一步的情况,这是不合法的。所以不会存在这种情况。
这样从修改的列的前一列三个会受到影响的位置往前推,推的过程中维护一下这段区间,显然它每一次的拓展不会超过 \(2\)。拓展到第一列时暴力修改一下 \(nxt\) 的新取值就可以了。复杂度 \(O(q(h+w) + hw)\),可以通过。
**E. Embedding Enumeration
大讨论题,把每个情况讨论出来还要各种画图于是瞬间不想写了(
丢个 别人的题解
M.CERC16
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | C | E | C | G | E | G | E | C | H | E | H |
B. Bipartite Blanket
**E. Easy Equation
这是一道解不定方程的题目。对于不定方程的解的讨论有一个常用方法是递降法,也就是从一个解得到一个“更小”的解。
对于本题,我们可以将递降法倒着做,从一个基本的、“最小”的解不断递增推导出大量的解。
通过样例观察可以得到一组显然的解是 \(1,k,k(k+1)\)。对于一组确定的解 \(a,b,c\),由于式子是二次的,故考虑固定 \(a,b\) 将原式化为与 \(c\) 相关的方程:
由于该方程有解,故由韦达定理 \(x_1+x_2=k(a+b)\),也就可以得到新的三元组 \(a,b,k(a+b)-c\)。对于其他两个元也可以类似处理,然后 bfs 求出 k 个合法解即可。
复杂度\(O(\)能过\()\)
N.CERC15
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | C | E | H | H | C | E | H | C | E | G |
O.CERC14
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | C | C | E | E | C | E | C | E | E | C | H | C |
P.CERC13
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | C | E | E | E | G | E | C | C | E | C | E | E |
Q.NWRRC17
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | E | C | H | C | H | H | E | C | E | E |
R.NWRRC16
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | C | E | E | C | E | E | G | H | H | E |
S.NWRRC15
| 编号 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | E | H | E | H | C | E | G | E | C | E |
**I. Insider's Information
要求每个三元组中 \(b_i\) 在 \(a_i\) 和 \(c_i\) 之间,实际上对于任意顺序只有前中后三种可能。
先考虑确定一个排列使得对于任意三元组,\(b_i\) 不是 \((a_i,b_i,c_i)\) 中最靠前的,去掉一种可能的情况。由于存在一个满足所有三元组的方案,所以这样的排列总是存在。构造方法是每一次拿出一个不作为任何三元组的 \(b_i\) 的位置,将以这个位置为 \(a_i\) 或 \(c_i\) 的三元组删掉。
然后从后往前将每个数加入答案序列里。考虑加入了当前数之后确定是否产生贡献的三元组,因为当前加入的数一定不是这些三元组的 \(b_i\),所以对于每个三元组,要么加在序列开头有 \(1\) 的贡献,要么加在序列结尾有 \(1\) 的贡献,选择贡献较大的一个即可。复杂度 \(O(n)\)。
T.NWRRC14
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | H | E | G | H | E | C | E | E | H |
*E. Expression
先建立用于正则表达式匹配的 NFA(非确定型有穷自动机)。它和 DFA 的唯一区别是对于一个点和一个字符,可以有多条对应的匹配出边;同时每一个点还有可能有空字符出边,表示走这一条边不需要匹配字符。
网上好像没什么人提到这玩意,大概是这样建的:
-
空串的 NFA 包含一个点,没有边,起始和终止状态都是它;
-
单个小写字符的 NFA 包含两个点,其中一个点向另一个点连一条对应字符的边,起始状态是边的入点,终止状态是边的出点;
-
一个单字符通配符 (.) 的 NFA 包含两个点,其中一个点向另一个点连 'a' 到 'z' 的边,起始状态是边的入点,终止状态是边的出点;
-
对于表达式 \(A\),设它的 NFA 为 \(F(A)\),则 \((A)*\) 的 NFA 就是在 \(F(A)\) 的基础上将起始状态和终止状态合并,也就是起始状态和终止状态之间互相连空字符边;
-
对于表达式 \(A,B\),设它们的 NFA 为 \(F(A),F(B)\),则 \(AB\) 的 NFA 就是从 \(F(A)\) 的终止节点向 \(F(B)\) 的起始节点连空字符边,新的 NFA 起始状态为 \(F(A)\) 的起始状态,终止状态为 \(F(B)\) 的终止状态;
-
对于表达式 \(A,B\),设它们的 NFA 为 \(F(A),F(B)\),则 \((A)|(B)\) 的 NFA 需要新建两个状态 \(x,y\),从 \(x\) 向两个 NFA 的起始状态连空字符边,从两个 NFA 的终止状态向 \(y\) 连空字符边,新的 NFA 的起始节点为 \(x\),终止节点为 \(y\)。
注意几个易错点:
-
有可能会出现 (|A) 或 (*) 这种参与运算是空串的阴间情况,注意判断,也可以在每个左括号读入的时候往前面加一个空串的 NFA;
-
\(*\) 符号可以选择读 0 次,所以从起始到终结也要连空字符边;
-
注意或运算的时候不要丢掉了其中参与空串的情况,有可能整个或运算中读空串是最优的,之前这里没写卡了一万年;
-
最开始写或的时候是把所有起始节点合成一个点、所有终止节点合成一个点,但这样如果有某个字符串带了 \(*\),则做完之后或上的所有字符串就都带上了 \(*\),所以是不正确的。
建完 NFA 了之后,注意到匹配 \(S\) 可以在 KMP 自动机上做,所以可以直接二维 dp \(f_{i,j}\) 表示在两个自动机的哪个节点。虽然时间没有问题,但空间爆炸了。
实际上可以将整个问题分成三段:从起始到即将匹配 \(S\)、匹配 \(S\)、匹配 \(S\) 完成后到终止。单独拎出中间部分可以把 KMP 自动机直接丢掉了。
那么先从起始跑一边 bfs、从终结反着跑一边 bfs,得到起始到所有点和所有点到终结的最短路,然后依次枚举 \(S\) 中的字符进行 dp,对于每个点计算 \(f_{i,j}\) 表示现在匹配的字符串的后缀是 \(S\) 的长度为 \(i\) 的前缀且匹配到 NFA \(j\) 号点的最短串长,因为你直到这里一定会匹配 \(S\) 所以前驱只需要记录从哪个 \(f_0\) 转移过来,可以滚动数组优化空间。这里转移的时候可以按照权值顺序 bfs 转移,复杂度就是单次 \(O(|E|)\) 的。
最后将两段拼起来就可以得到答案了,bfs 的时候记录一下前驱容易还原方案。复杂度 \(O(|E|(|S| + \Sigma))\)。
U.NWRRC13
| 编号 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 评价 | E | E | C | E | E | E | E | H | C | H | E |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号