AGC041F Histogram Rooks
有生之年自己做出了一个 AGC F 还踩了标算，但是好像在我之前已经有人踩过标算了，再鞭尸一波也无可厚非 hhh
看到“全部被覆盖” 条件不好做，考虑容斥，即选择若干个位置强制它们不覆盖，那么会有位置不能放车，而其余的位置可以选择放或者不放，方案数可以计算。但暴力枚举不优秀。在后文中为了描述方便定义行连续段表示的是某一行中不包含被删掉的格子的极长格子段，列连续段同理。
注意到这个网格的行并不连续（即对于某个确定的行，其行连续段可能有多个），但列是连续的（即第 \(i\) 列只有 \(1 \sim h_i\) 这一个列连续段）。那么如果确定了某些列上存在格子没有覆盖，那么这些列上的所有格子一定不能放车。
考虑枚举存在位置强制不覆盖的列的集合 \(S\)，那么这些列的所有格子就不能放车。此时对于一个长为 \(len\)、有 \(p\) 个位置所在的列是强制不覆盖的列的行连续段，枚举这一行上的 \(p\) 个位置有哪一些位置选择了强制不覆盖，有两种情况：
- 在这个行上没有任何位置选择强制不覆盖，那么剩余 \(len-p\) 个位置能自由选择，方案数为 \(2^{len-p}\)；
- 在这个行上存在位置选择强制不覆盖，此时这行不能放车，方案数为 \(1\)。枚举有多少个位置选择强制不覆盖，乘上容斥系数贡献是 \(\sum\limits_{j=1}^p (-1)^j \binom{p}{j}\)。
那么这一个行连续段对答案的贡献就是 \(2^{len-p} + \sum\limits_{j=1}^p (-1)^j \binom{p}{j}\)。注意到 \(\sum\limits_{j=1}^p (-1)^j \binom{p}{j} = -[p \neq 0]\)，可以改写贡献为 \(2^{len-p} - [p \neq 0]\)。最后将所有贡献的答案乘起来。
然而上面的做法存在问题，因为无法确定强制选择了位置没有覆盖的列在方案中是否确实选择了强制不覆盖的格子。如果某一列并没有选择会导致方案的算重。
所以继续考虑容斥，在枚举集合 \(S\) 的基础上枚举 \(S\) 最后没有选择强制不覆盖格子的子集 \(T\) ，容斥系数是 \((-1)^{|T|}\)。
这样某个行连续段中如果存在 \(p\) 个位置所在的列在集合 \(S\) 中，有 \(q\) 个位置所在的列在集合 \(T\) 中，方案数将变为 \(2^{len-p} - [p \neq q]\)。值得注意的是虽然集合 \(T\) 对应的列集合不存在任何格子选择不覆盖，但是仍然需要认为这些列的所有格子无法放置，否则无法达到容斥效果。
这样就可以正确地算出答案了。
这玩意显然太慢。为了优化可以注意到以下若干性质：
- 计算某个行连续段的贡献只关心两个量：\(p\) 和 \([p \neq q]\)。
- \(p \geq q\)，所以 \([p \neq q] = [p - q > 0]\)
- 对于左端点所在列相同、右端点所在列相同的两个行连续段，它们的贡献一定相同。把所有这样的行连续段看成一个集合，那么这样的集合最多只有 \(N\) 个，而且一个集合内所有行连续段的所在行一定是连续的若干行。
简单来说看一张图就好，下面这个图里相同颜色的所有行连续段的贡献显然是相同的，可以一起计算，且可以简单证明这样的颜色数量至多为 \(N\)。
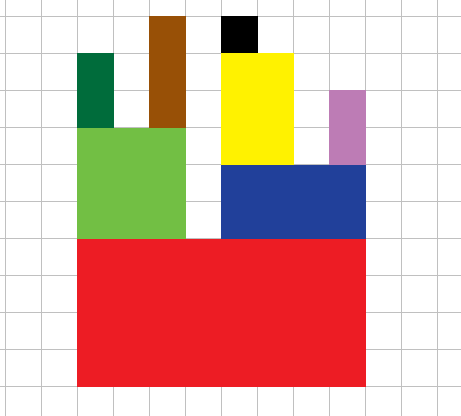
找这样的矩形只需要在初始图中找到 \(h\) 最小的若干列，再通过这些列将原图划分为若干个子部分，每个部分递归处理。
而且还可以发现一个事情：
上图中对于红色的行，其覆盖的所有列中在集合 \(S\) 中的列的数量 = 浅绿色覆盖的所有列中在集合 \(S\) 中的列的数量 + 蓝色覆盖的所有列中在集合 \(S\) 中的列的数量 + 第 4 列是否在集合 \(S\) 中。
这是一个类似于子问题的结构，也就是说某种颜色覆盖的列的数量等于其正上方所有其他颜色矩形覆盖的列的数量加上其独有的数量。
（注：这里的正上方指的是在上方而且存在重合的边界）
给每一个矩形一个标号，并认为如果矩形 \(A\) 在矩形 \(B\) 的正上方则 \(A\) 是 \(B\) 的儿子。
设计一个 DP：\(f_{i,j,0/1}\) 表示在 \(i\) 号矩形中，其覆盖的列有 \(j\) 列在集合 \(S\) 中，且是否存在某一列在集合 \(S\) 却不在集合 \(T\) 中，在这样的情况下所有方案中这个矩形和在它上方的所有矩形的方案数的总和。转移先从儿子处将该数组合并，再考虑其独有的若干列的选择，最后乘上每行如何放车的系数。因为每行的方案一致所以复杂度可以做到 \(O(N^2 \log N)\)，而所有可能的转移系数只有 \(O(N)\) 种，通过预处理可以将复杂度优化为 \(O(N^2)\)。
