CSP 模拟 32

noip23 ZR二十连测 DAY 10

A 奇观

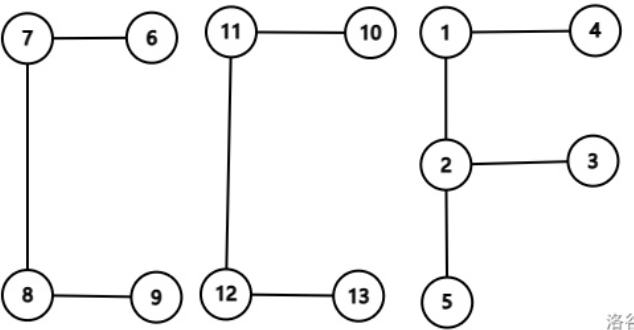
C，C，F 显然是互相独立的，设 \(C\) 为 C 的数量，\(F\) 为 F 的数量，那么答案显然就是 \(CCF\)。
设 \(d_i\) 表示节点 \(i\) 的度数，\(out_i\) 表示节点 \(i\) 扩展两个的方案数，显然有 \(out_i=\sum_{(i,j)\in \text{E}}d_j\)，对于 C 考虑以上图 7 的位置为基准点，对于 \(i\) 做位置 7 的方案数就是 \(d_i\cdot out_i\)，对于 \(i\) 做 F 中 2 位置的方案数就是 \(d_i\cdot d_i\cdot out_i\)，由于是完全图，知道删边后就能求出 \(d_i\)，对于 \(out_i\) 容斥减去不相连的 \(d_j\) 即可。时间复杂度 \(\mathcal{O}(n+m)\)，作为签到题来说质量不错。

B 铁路

简单观察发现初始的 \(ans=n\)，每次操作后的答案就变成了 \(ans\) 减去询问的两点之间的距离。
做法一：发现虚点没有任何作用，只需要他的映射即可。问题就变成了两点距离查询，两点间边权推平为 0，自然想到树剖，垃圾 OJ 跑不动俩 log 咋办，可以对于每一条链建线段树，这样查询只会在端点处查询，中间都是全局查，时间复杂度 \(\mathcal{O}(n\log n)\)。
做法二：树剖线段树太长了，我懒得写咋办。那直接抛弃这两个，考虑每次暴跳，把跳的点合并，因为每个点只会跳一次，所以这里的时间复杂度是 \(\mathcal{O}(n)\)，合并直接用并查集，每次向父亲去合并，简单好写，整体时间复杂度近似线性。

C 光纤

很简单，但是计算几何 😅️😅️

引理：到若干个点的距离最大值最小的直线一定平行于这些点构成的凸包的一条边。

考虑如下情况

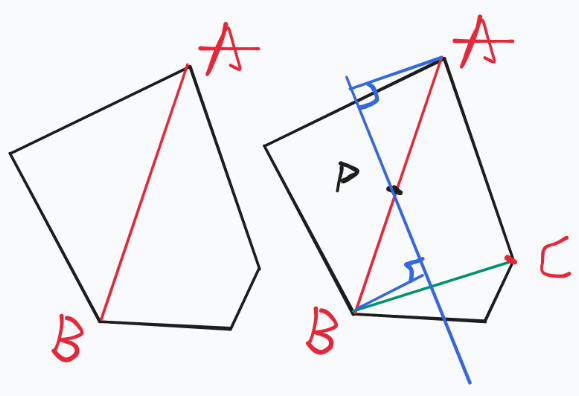
证明：钦定 A 和 B 为答案的贡献点，则 A 和 B 到答案直线的距离一定相等，所以答案直线一定过 AB 中点 P，考虑 A 点的临界点 C，C 到直线的距离一定小于 A 到直线的距离，如图，当直线与 AC 平行时，A 和 C 到直线的距离相等，此时将直线逆时针旋转，A 到直线的距离会增大，答案更劣，将直线顺时针旋转，A 到直线距离减小，但是 C 到直线距离增大，违反了 A 和 B 点是答案贡献点的前提，故当直线平行于 AC 时，答案最小，所以到若干个点的距离最大值最小的直线一定平行于这些点构成的凸包的一条边。
根据引理，直接旋转卡壳求出最小答案，时间复杂度 \(\mathcal{O}(n\log)\)，瓶颈在建立凸包。
这题如果封装有理数类就太难写了，调了一天，放弃写了 long double，一会就调过了。

#include<bits/stdc++.h>
typedef __int128 LL;
#define int LL
typedef long long ll;
typedef unsigned long long ull;
inline int read(){char ch=getchar();int x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);return x*f;}
inline void write(LL x){if(x>=10)write(x/10);putchar(x%10+48);}
const int N=1e6+10;
int n,s[N],top;
bool vis[N];
struct NODE{long double x,y;}a[N],p[N];
struct VCT{
    long double x,y;
    inline VCT(NODE a,NODE b){x=b.x-a.x,y=b.y-a.y;}
    inline long double operator*(VCT b){long double res=(x*b.y)-(y*b.x);return res;}
};
struct ANS{long double ds;int a,b,c;}ans;
inline long double dis(NODE a,NODE b,NODE c){
    if(c.x-b.x==0){long double res=(c.x-a.x)*(c.x-a.x);return res;}
    long double AA=(c.y-b.y)/(c.x-b.x);
    long double CC=c.y-AA*c.x;
    long double BB=-1;
    long double zc=(AA*a.x)+(BB*a.y)+CC;
    long double res=zc*zc/((AA*AA)+(BB*BB));
    return res;
}
struct C;
inline void check(C&);
struct C{
    LL x,y;
    inline C operator+(C b){LL gcd=std::__gcd(y,b.y),lcm=y*b.y/gcd;C res={lcm/y*x+lcm/b.y*b.x,lcm};check(res);return res;}
    inline C operator-(C b){LL gcd=std::__gcd(y,b.y),lcm=y*b.y/gcd;C res={lcm/y*x-lcm/b.y*b.x,lcm};check(res);return res;}
    inline C operator*(C b){LL gcd1=std::__gcd(x,b.y),gcd2=std::__gcd(y,b.x);return{(x/gcd1)*(b.x/gcd2),(y/gcd2)*(b.y/gcd1)};}
    inline C operator/(C b){return *this*C{b.y,b.x};}
    inline bool operator<(C b){LL gcd=std::__gcd(y,b.y),lcm=y*b.y/gcd;return lcm/y*x<lcm/b.y*b.x;}
    inline bool operator<=(C b){LL gcd=std::__gcd(y,b.y),lcm=y*b.y/gcd;return lcm/y*x<=lcm/b.y*b.x;}
    inline bool operator==(C b){return (x==b.x)&&(y==b.y);}
};
inline C G(int k){return{k,1};}
inline void check(C &a){int gcd=std::__gcd(a.x,a.y);a.x/=gcd,a.y/=gcd;if(a.y<0)a.x*=-1,a.y*=-1;}
inline void out(C x){write(x.x);putchar('/');write(x.y);putchar('\n');}
inline void FINAL(NODE a,NODE b,NODE c){
    if(c.x-b.x==0){C res={(c.x-a.x)*(c.x-a.x),4};check(res);out(res);return;}
    C AA={c.y-b.y,c.x-b.x};check(AA);
    C CC=G(c.y)-AA*G(c.x);check(CC);
    C BB=G(-1);
    C zc=(AA*G(a.x))+(BB*G(a.y))+CC;
    check(zc);
    C res=zc*zc/((AA*AA)+(BB*BB));
    res.y*=4;
    check(res);
    out(res);
}
signed main(){
    freopen("a.in","r",stdin);freopen("a.out","w",stdout);
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    n=read();
    if(n<=2){std::cout<<"0/1\n";exit(0);}
    for(int i=1;i<=n;++i)a[i].x=read(),a[i].y=read();
    std::sort(a+1,a+n+1,[](NODE a,NODE b){return a.x==b.x?a.y<b.y:a.x<b.x;});
    s[++top]=1;
    for(int i=2;i<=n;++i){
        while(top>=2&&VCT(a[s[top-1]],a[s[top]])*VCT(a[s[top]],a[i])<=0)vis[s[top--]]=0;
        s[++top]=i;vis[i]=1;
    }
    int tmp=top;
    for(int i=n-1;i;--i){
        if(vis[i])continue;
        while(top>tmp&&VCT(a[s[top-1]],a[s[top]])*VCT(a[s[top]],a[i])<=0)vis[s[top--]]=0;
        s[++top]=i;vis[i]=1;
    }
    for(int i=1;i<=top;++i)p[i]=a[s[i]];
    for(int i=1;i<top;++i)a[i]=p[i];
    for(int i=top;i<=top*2-2;++i)a[i]=p[i-top+1];
    int len=top*2-2;
    int l=2;
    ans={1e30,2,1,1};
    for(int i=1;i<top;++i){
        while(l<len&&(dis(a[l],p[i],p[i+1])<=dis(a[l+1],p[i],p[i+1])))l++;
        long double zc=dis(a[l],p[i],p[i+1]);
        if(ans.ds>zc)ans={zc,l,i,i+1};
    }
    FINAL(a[ans.a],p[ans.b],p[ans.c]);
}

D 权值

不会。
赛时疯狂降智，T1 被吓到，T2 想出树剖后疯狂调试，没去想别的，T3 不会，T4 不会。浪费了很长时间，没有去打暴力分。