P2437 蜜蜂路线

P2437 蜜蜂路线

题目描述

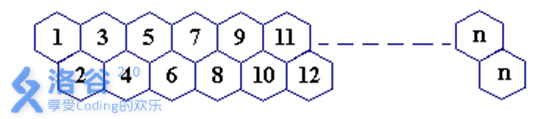
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 \(m\) 开始爬到蜂房 \(n\)，\(m<n\)，有多少种爬行路线？（备注：题面有误，右上角应为 \(n-1\)）

输入格式

输入 \(m,n\) 的值

输出格式

爬行有多少种路线

样例

输入

1 14

输出

377

提示

对于100%的数据，\(1 \le M,N\le 1000\)

---

思路一

由题目可知，蜜蜂要想走到 \(i\) 号蜂房，那么它可以从 \(i-1\) 号蜂房走一步或从 \(i-2\) 号蜂房走两步，用 \(f \lbrack i \rbrack\) 表示走到 \(i\) 号蜂房的方案数，则 \(f \lbrack i \rbrack=f \lbrack i-1 \rbrack+f \lbrack i-2 \rbrack\)。易看出：方案数为斐波那契数列。当 \(i\) 大于 \(90\)，\(f \lbrack i \rbrack\) 的值就超出了长整型范围，题目中 \(i\) 可取到的最大值为 \(1000\)，因此需要使用高精度算法。

一开始蜜蜂在 \(m\) 号蜂房，走到 \(m\) 号蜂房的方案数为 \(1\)，走到 \(m+1\) 号蜂房的方案数也为 \(1\)，可以设为斐波那契数列的初始值。枚举 \(m+2\) 到 \(n\) 的斐波那契数列。接下来的代码，先用数组形式的高精度加法运算，数组 \(a,b,c\) 分别用来迭代斐波那契数列的每一项。需要注意以下几点：

1. 迭代过程需要每次清空数组 \(c\)；
2. 答案可能为 \(0\)，因此需要特判；
3. 答案有可能输出第 \(m\) 项和第 \(m+1\) 项，可以特判。

代码

#include <bits/stdc++.h>

using namespace std;

int m, n, a[1010], b[1010], c[1010], lena, lenb, lenc;

void add()
{
	lenc = max(lena, lenb);
	for (int i = 1; i <= lenc; i ++ )
	{
		c[i] += a[i] + b[i];
		c[i + 1] = c[i] / 10;
		c[i] %= 10;
	}
	if (c[lenc + 1])
		lenc ++;
}

int main()
{
	scanf("%d %d", &m, &n);
	a[1] = 1;
	lena = 1;
	b[1] = 1;
	lenb = 1;
	if (n == 0) // 特殊数据
	{
		puts("0");
		return 0;
	}
	if (n == m)
	{
		puts("1");
		return 0;
	}
	if (n == m + 1)
	{
		puts("1");
		return 0;
	}
	for (int i = m + 2; i <= n - 1; i ++ )
	{
		add();
		memcpy(a, b, sizeof(b));
		lena = lenb;
		memcpy(b, c, sizeof(c));
		lenb = lenc;
		memset(c, 0, sizeof(c));
	}
	add();
	for (int i = lenc; i >= 1; i -- )
		printf("%d", c[i]);
	return 0;
}

---

思路二

结构体和重载运算符的方式。结构体变量为数组 \(f\)，其属性包含斐波那契数列每一项数字的长度，及该数字各个位的数值。重载加号，递推方式：“\(f \lbrack i \rbrack=f \lbrack i-1 \rbrack+f \lbrack i-2 \rbrack\)”，记录斐波那契的每一项，最后输出 \(f \lbrack n \rbrack\) 的值。由于每一项都保留下来了，因此可以不必特判第 \(m\) 项和第 \(m+1\) 项。

代码

#include <bits/stdc++.h>

using namespace std;

int m, n;

struct node
{
	int len, s[5010];
	node()
	{
		len = 0;
		memset(s, 0, sizeof(s));
	}
} f[1010];

node operator + (node &a, node &b)
{
	node c;
	c.len = max(a.len, b.len);
	for (int i = 1; i <= c.len; i ++ )
	{
		c.s[i] += a.s[i] + b.s[i];
		c.s[i + 1] = c.s[i] / 10;
		c.s[i] %= 10;
	}
	if (c.s[c.len + 1])
		c.len ++;
	return c;
}

void print(node a)
{
	for (int i = a.len; i >= 1; i -- )
		printf("%d", a.s[i]);
}

int main()
{
	scanf("%d %d", &m, &n);
	if (n == 0)// 特殊数据
	{
		puts("0");
		return 0;
	}
	f[m].s[1] = 1;
	f[m].len = 1;
	f[m + 1].s[1] = 1;
	f[m + 1].len = 1;
	for (int i = m + 2; i <= n; i ++ )
		f[i] = f[i - 1] + f[i - 2];
	print(f[n]);
	return 0;
}