P2241 统计方形（数据加强版）

P2241 统计方形（数据加强版）

题目

有一个 \(n \times m\) 方格的棋盘，求其方格包含多少正方形、长方形（不包含正方形）。

输入

一行，两个正整数 \(n,m\)（\(n \le 5000,m \le 5000\)）。

输出

一行，两个正整数，分别表示方格包含多少正方形、长方形（不包含正方形）。

样例

输入

2 3

输出

8 10

---

思路

根据题意得到如下棋盘，假设长为 \(X\)，宽为 \(Y\)。

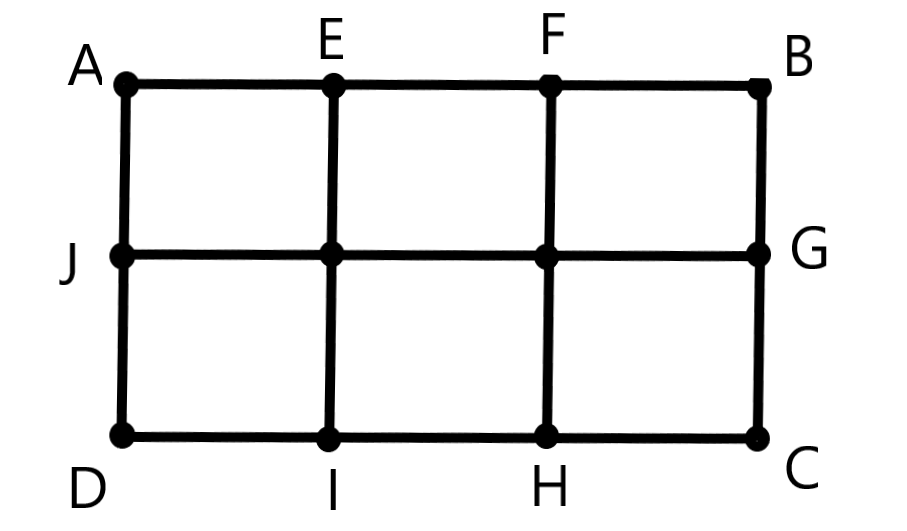
尝试直译枚举对象，即枚举矩形的左下角和右上角坐标，统计数量，时间复杂度是枚举矩形左下角横坐标、左下角纵坐标、右上角横坐标、右上角纵坐标之积，为 \(O(n^2m^2)\)，显然超时。

进一步思考如何减少枚举数量，如果只枚举矩形的一个顶点坐标，同时枚举边长，因统计正方形和长方形的数量，依然要枚举四个变量，枚举顶点坐标的方式可行性不佳。

换一种思路，枚举边长。矩形对边平行且相等，求棋盘包含长为 \(x\)，宽为 \(y\)（\(x,y\) 假设已知）的小矩形数量。在棋盘内最多可以画长度为 \(x\) 的长边 \(X-x+1\) 条，例如 \(X=3,x=2\)，小矩形的长边最多可以画 \(2\) 条。同理在棋盘内最多可以画长度为 \(y\) 的短边 \(Y-y+1\) 条。长为 \(x\) 和宽为 \(y\) 可组成 \((X-x+1) \times (Y-y+1)\) 个小矩形。因此可枚举小矩形的长和宽，枚举范围从 \(0\) 到棋盘长/宽。其中包含正方形和长方形。如果 \(x\) 与 \(y\) 相等，则为正方形，如果不等则为长方形，满足条件的统计即可。

由于数据范围中 \(n,m \le 5000\)，枚举矩形长、宽相乘以后可能超过 \(\operatorname{int}\) 范围，因此代码中统计变量使用 \(\operatorname{long long}\) 类型。

---

代码

#include <bits/stdc++.h>

using namespace std;

int X, Y;
long long a, b;

int main()
{
	cin >> X >> Y;
	for (int x = 1; x <= X; x ++ )
	{
		for (int y = 1; y <= Y; y ++ )
		{
			if (x == y)
				a += (X - x + 1) * (Y - y + 1);
			else
				b += (X - x + 1) * (Y - y + 1);
		}
	}
	cout << a << ' ' << b << '\n';
	return 0;
}