DS博客作业04--图
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 胡旻轩 |
0.PTA得分截图

1.本周学习总结

1.1 图的存储结构
1.1.1 邻接矩阵

邻接矩阵的结构体定义
#define MAXV<最大顶点数>
typedef struct {
int no;//顶点编号
INfoType info;//顶点其他信息
}VertcxRype;
typedef struct {
int edges[MAXV][MAXV];//邻接矩阵
int n, e;//顶点数,边数
VertcxRype vexs[MAXV];//存放顶点信息
}MatGraph;
建图函数
void CreateMGraph(MGraph &g, int n, int e)//建图
{
//n顶点,e弧数
g.n = n;
g.e = e;
int i, j;
int a, b;//下标
for (i = 1; i <= n; i++)//先进行初始化
{
for (j = 1; j <= n; j++)
{
g.edges[i][j] = 0;
}
}
for (i = 1; i <= e; i++)//无向图
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
}
1.1.2 邻接表
邻接矩阵的结构体定义
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph; //邻接表类型
建图函数
void CreateAdj(AdjGraph*& G, int n, int e) //创建图邻接表
{
int i, j, a, b;
int A[MAXV][MAXV];
ArcNode* p;
G = (AdjGraph*)malloc(sizeof(AdjGraph));//申请动态储存
for (i = 0; i <= n; i++)//邻接表头指针指针置零
{
G->adjlist[i].firstarc = NULL;
}
for (i = 0; i < n; i++)//邻接矩阵初始化置零
{
for (j = 0; j <= n; j++)
{
A[i][j] = 0;
}
}
for (i = 0; i < e; i++)//邻接矩阵对应边置1
{
cin >> a >> b;
A[a][b] = 1; A[b][a] = 1;
}
//查找邻接矩阵中的每个元素
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
if (A[i][j])
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j; //存放临节点
p->info = A[i][j]; //放权值
p->nextarc = G->adjlist[i].firstarc; //头插法插入节点
G->adjlist[i].firstarc = p; //
}
}
}
G->n = n; G->e = e;
}
1.1.3 邻接矩阵和邻接表表示图的区别
1)当数据中的边关系不是很复杂时,即图为稀疏图时,有很多的空间是没用的,这时候用链表就能省下很多空间。
2)而当图为稠密图的时候,顶点之间都有边关系,这时候用矩阵更合适。
3)时间复杂度:邻接矩阵时间复杂度为O(n的平方),邻接表的时间复杂度为o(n+e)。
1.2 图遍历
1.2.1 深度优先遍历
- 例:

对上无向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问B(A的邻接点,由储存结构决定的)。
第3步:访问G(B的邻接点)。 和B相连只有"G"(A已经访问过了)
第4步:访问E(G的邻接点)。 在第3步访问了B的邻接点G之后,接下来应该访问G的邻接点,即"E和H"中一个(B已经被访问过,就不算在内)。而由于E在H之前,先访问E。
第5步:访问C(E的邻接点)。 和E相连只有"C"(G已经访问过了)。
第6步:访问D(C的邻接点)。
第7步:访问H。因为D没有未被访问的邻接点;因此,一直回溯到访问G的另一个邻接点H。
第8步:访问(H的邻接点)F。
因此访问顺序是:A -> B -> G -> E -> C -> D -> H -> F
深度遍历代码
- 邻接矩阵
void DFS(MGraph g, int v)//邻接矩阵深度遍历
{
if (flag == 0)
{
cout << v;
flag = 1;
}
else
cout << " " << v; //输出顶点
visited[v] = 1;//标记已访问该节点
for (int i = 1; i <= g.n; i++)
{
if(g.edges[v][i] == 1 && visited[i] == 0)
{
DFS(g, i); //当前顶点与 i 顶点邻接且未被访问,递归搜索
}
}
}
- 邻接表
void DFS(AdjGraph *G, int v)//v节点开始深度遍历
{
visited[v] = 1;
ArcNode *p;//新建结点储存当前信息
if (flag == 0)
{
cout << v;
flag = 1;
}
else
{
cout << " " << v;
}
p = G->adjlist[v].firstarc;
while (p != NULL)//遍历当前链
{
if (visited[p->adjvex] == 0)//判断未访问过
{
DFS(G, p->adjvex);
}
p = p->nextarc;
}
}
深度遍历适用哪些问题的求解
可以找到两点之间的全部路径,以此可以找到迷宫问题
可以判断是否有简单路径,测试图的结构是否正确。
1.2.2广度优先遍历
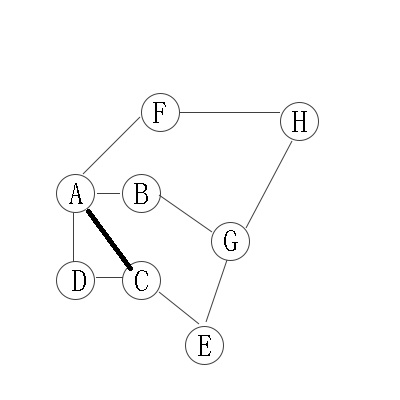
从A开始,有4个邻接点,“B,C,D,F”,这是第二层;
在分别从B,C,D,F开始找他们的邻接点,为第三层。以此类推。
因此访问顺序是:A -> B -> C -> D -> F -> G -> E -> H
- 广度遍历代码
邻接矩阵
void BFS(MGraph g, int v)//邻接矩阵广度遍历
{
int t;
queue<int>q;
if (visited[v] == 0)
{
cout << v;
visited[v] = 1;
q.push(v);
}
while (!q.empty())
{
t = q.front();
q.pop();
for (int j = 1; j <= g.n; j++)
{
if (g.edges[t][j] == 1 && visited[j] == 0)
{
cout << " " << j;
visited[j] = 1;
q.push(j);
}
}
}
}
邻接表
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
queue<int>q;
ArcNode* node;
int n;//边的序号
int j;
visited[v] = 1;//表示已访问
cout << v ;
q.push(v);//入队
while (!q.empty())//队不空
{
j = q.front();
q.pop();
node = G->adjlist[j].firstarc;
while (node)//按邻接表输出头结点后的所有节点
{
if (!visited[node->adjvex])
{
visited[node->adjvex] = 1;
cout << " " << node->adjvex;
q.push(node->adjvex);
}
node = node->nextarc;
}
}
}
- 广度遍历适用哪些问题的求解。
最短路径
最远顶点
最短单词路径等
1.3 最小生成树
最小生成树:
- (1)一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
- (2)就是一条路联通所有结点,且边长度合是最短的。
1.3.1 Prim算法求最小生成树
如图所示prim来生成最小数:
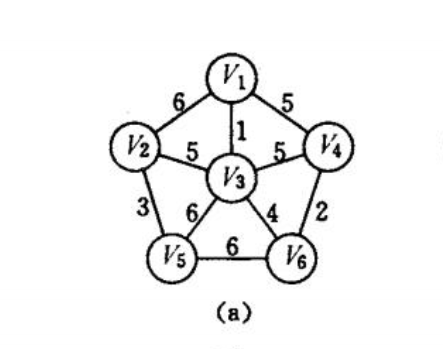
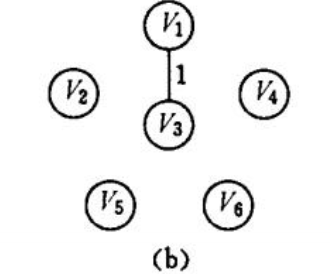
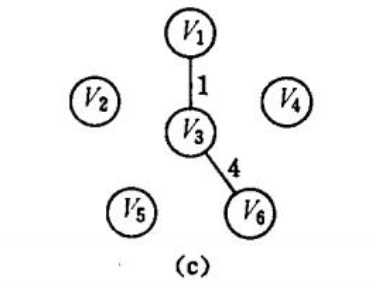
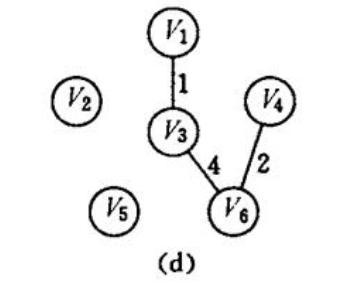
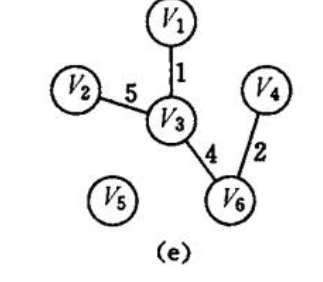

使用Prim算法要借助两个数组做工具,一个是lowcost[]//存放候选边,每个顶点到u中最小边。
另一个是closet[]//U中顶点的邻边顶点
Prim代码:
void Peim(MGraph g, int v)
{
int lowcost[MAXV];
int min;
int closest[MAXV];
int i, j, k;
for (i = 0; i < g.n; i++)
{
lowcost[i] = g.edges[v][i];//置初值,放入顶点v和所有顶带你的权值
closest[i] = v;
}
for (i = 1; i < g.n; i++)//n-1条边,进行n-1次
{
min = INF;
for (j = 0; j < g.n; j++)//遍历找到权值最小的
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
k = j;//记录下标
}
}
lowcost[k] = 0;//lowcost为0表示该顶点已使用
for (j = 0; i < g.n; j++)//遍历所有顶点,比较找到的顶点与其他顶点的权值是否比原来小
{
if (lowcsost[j] != 0 && g.edges[k][j] < lowcost[j])
{
lowcost[j] = g.edges[k][j];
closest[j] = k;//改变权值和相邻的顶点
}
}
}
}
1.3.2 Kruskal算法求解最小生成树
操作如下图所示:

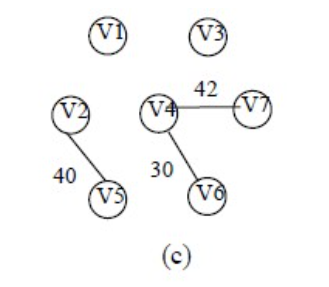
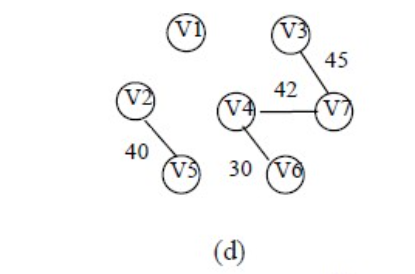
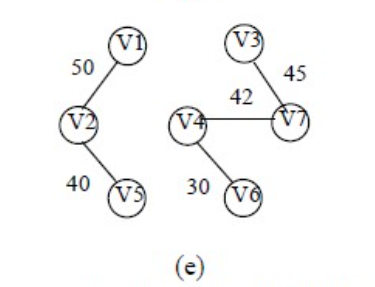

Kruskal代码如下:
typedef struct {
int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
}Edge;
//改进的克鲁斯卡尔算法(使用了堆排序,并查集)
void Kruskal(AdjGraph* g)
{
int i,j,k,u1,v1,sn1,sn2;
UFSTree t[MAXSize]; //并查集,树结构
ArcNode* p;
Edge E[MAXSize];
k=1; // E数组的下标从1开始计
for(i = 0; i < g.n; i++)
{
p=g->adjlist[i].firstarc;
while(p!=NULL)
{
E[k].u=i;
E[k].v=p->adjvex;
E[k].w=p->weight;
k++;
p=p->nextarc;
}
}
HeapSort(E,g.e); //采用堆排序对E数组按权值递增排序
MAKE_SET(t,g.n); //初始化并查集树t
k=1; //k表示当前构造生成树的第几条边,初值为1
j=1; //E中边的下标,初值为1
while(k<g.n) //生成的边数为n-1
{
u1=E[j].u;
v1=E[j].v; //取一条边的头尾顶点编号u1和v1
sn1=FIND_SET(t,u1);
sn2=FIND_SET(t,v1); //分别得到两个顶点所属的集合编号
if(sn1!=sn2) //两顶点属不同集合
{
k++; //生成边数增1
UNION(t, u1, v1); //将u1和v1两个顶点合并
}
j++; //下一条边
}
}
克鲁斯卡尔算法:按权值的递增顺序选择合适的边来构造最小生成树,选取的边不能使生成树形成回路。
克鲁斯卡尔算法的时间复杂度为O(elog2e)。由于它只与边的条数e有关,所以克鲁斯卡尔算法适合于稀疏图,图的存储结构为邻接表。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
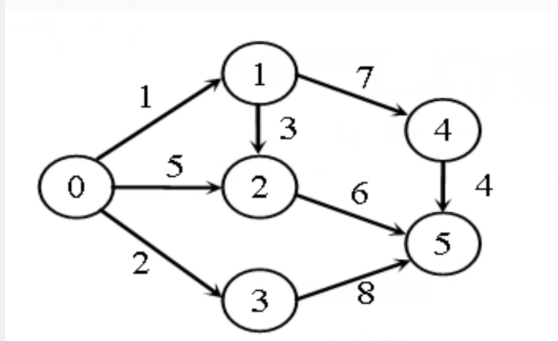

Dijkstra算法如何解决贪心算法无法求最优解问题?展示算法中解决的代码
void Dijkstra(MatGraph g, int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];//判断是否访问
int mindis, i, j, u;
for (i = 0; i < g.n; i++)
{
dist[i] = g.edges[v][i];//初始化距离
s[i] = 0;
if (g.edges[v]]i] < INF)//v到i有边,初始化前继结点
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
s[v] = 1;
for (i = 0; i < g.n; i++)//进行n-1次
{
mindis = INF;
for (j = 0; j < g.n; j++)//找到最小路径的长度
{
if (s[j] == 0 && dist[j] < mindis)
{
u = j;
mindis = dist[j];
}
}
s[u] = 1;
for (j = 0; j < g.n; j++)//修改改变结点后的路径长度
{
if (s[j] == 0)
{
if (g.edges[u][j] < INF&&dist[u] + g.edges[u][j] < dist[j])//修改此处可得到各种多种解法
{
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
}
}
}
算法中涉及到要循环n次(顶点个数)直到所有顶点的最短路径都求出来,且在循环中又要循环n次以来选取不在S中(即在U中)
的顶点且具有求小最短路径长度的顶点,这里用了两层循环,考虑最坏情况,时间复杂度为O(n^2).
Dijkstra算法更适用于邻接矩阵结构。
1.4.2 Floyd算法求解最短路径
Floyd算法解决什么问题?
是解决给定的加权图中顶点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包
例如:求解几座城市之间的最短距离,以及最短距离所经过的城市。
Floyd算法需要哪些辅助数据结构?
Floyd需要A和path两个二维数组,其中A数组是用于存放两个顶点之间的最短路径,path数组用于存放其的前继结点。
Floyd算法优势,举例说明。
Floyd算法,是一种动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,
效率要高于执行|V|次Dijkstra算法。可以算出任意两个节点之间的最短距离,代码编写较为简单。
算法代码
#include<stdio.h>
#include<stdlib.h>
#define max 1000000000
int d[1000][1000],path[1000][1000];
int main()
{
int i,j,k,m,n;
int x,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++){
d[i][j]=max;
path[i][j]=j;
}
for(i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
d[x][y]=z;
d[y][x]=z;
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++) {
if(d[i][k]+d[k][j]<d[i][j]) {
d[i][j]=d[i][k]+d[k][j];
path[i][j]=path[i][k];
}
}
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
if (i!=j) printf("%d->%d:%d\n",i,j,d[i][j]);
int f, en;
scanf("%d%d",&f,&en);
while (f!=en) {
printf("%d->",f);
f=path[f][en];
}
printf("%d\n",en);
return 0;
}
1.5 拓扑排序

排序方法:
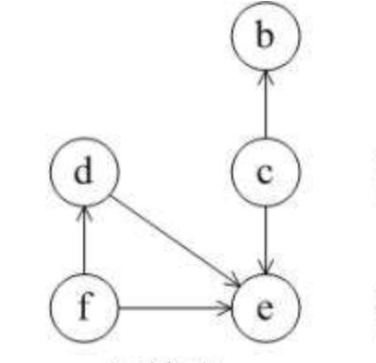
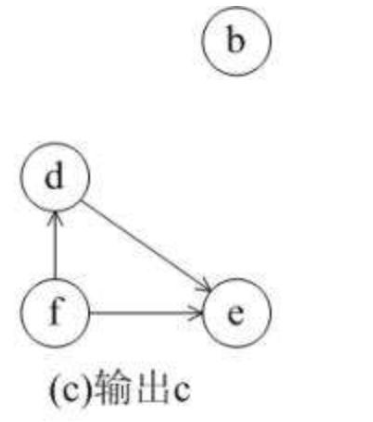
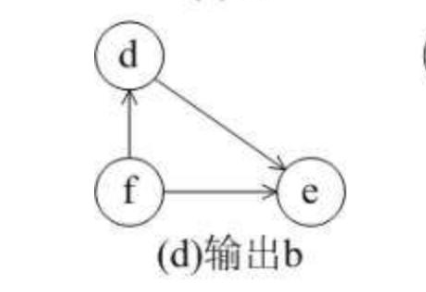

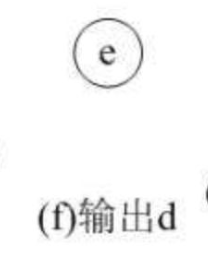
故拓扑排序为acbfde
伪代码
while(栈不空)
{
出栈v,访问;
遍历v所有邻接点
{
所有邻接点的入度-1
当入度为0时,则入栈,以此实现入度为0时的删除操作
}
}
拓扑排序代码
void TopoSort(ALGraph* G, int n)
{
int i, j, k, top, m = 0;
EdgeNode* p;
int* d = (int*)malloc(n * sizeof(int));
for (i = 0; i < n; i++) //初始化数组
{
d[i] = 0;
}
for (i = 0; i < n; i++) //统计各个顶点的入度情况,并把他们填入数组里面
{
p = G->adjlist[i].firstedge;
while (p != NULL)
{
j = p->adjvex;
d[j]++;
p = p->next;
}
}
top = -1;
for (i = 0; i < n; i++) //先找出里面入度是0的顶点
{
if (d[i] == 0)
{
d[i] = top;
top = i;
}
}
while (top != -1)
{
j = top;
top = d[top];
printf("%d ", j);
m++; //统计顶点
p = G->adjlist[j].firstedge;
while (p)
{
k = p->adjvex; //相l连接的顶点
d[k]--; //相连接的顶点入度减1
if (d[k] == 0) //如果发现入度为0的新顶点,从该顶点出发
{
d[k] = top;
top = k;
}
p = p->next;
}
}
if (m < n) printf("\n有回路!\n");
free(d);
}
2.PTA实验作业
2.1 六度空间
伪代码:
int BFS(MGraph g,int v)//广搜
{
int w;
int tail,last;
int count=0,level=0;
int visited[MAXV]={0};
queue<int> q;
源点v入队列,同时标记v已访问过;
用last标记顶点v;
空间加一;
while(q不空) do
int j;
对头元素出队,w=q.front(),队列长度减一;
for j=1 to g.n do
if visit[j]==0&&g.edges[w][j] then
顶点j入队列,且标记已访问;
用tail标记顶点v,记录当前圈的最后一个顶点编号;
空间加一;
end if
end for
if 遍历一圈即 last == temp then
层数加一,并记录当前层的最后一个顶点;
if 遍历6层即level=6 then
break;
end while
}
代码截图
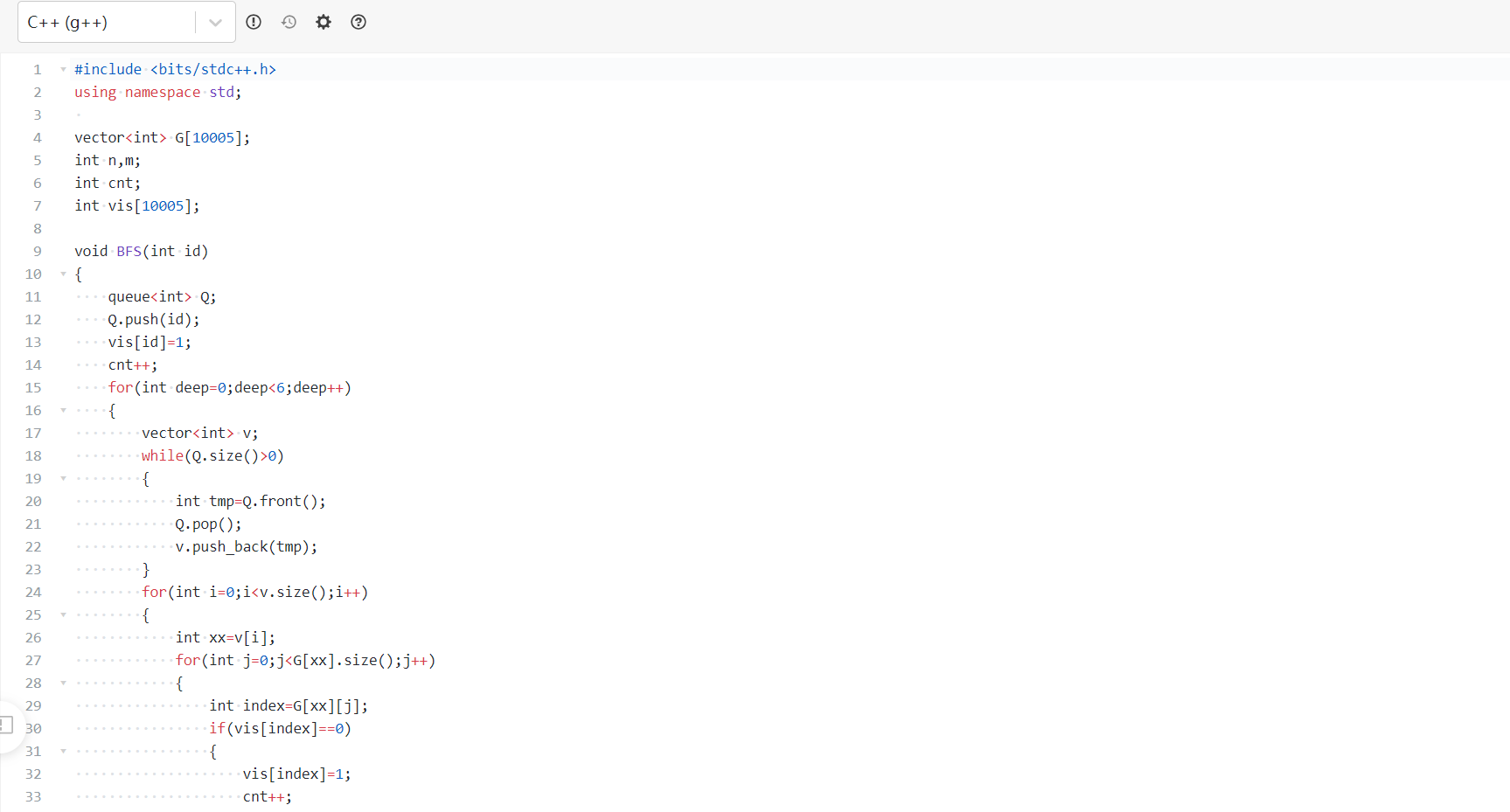
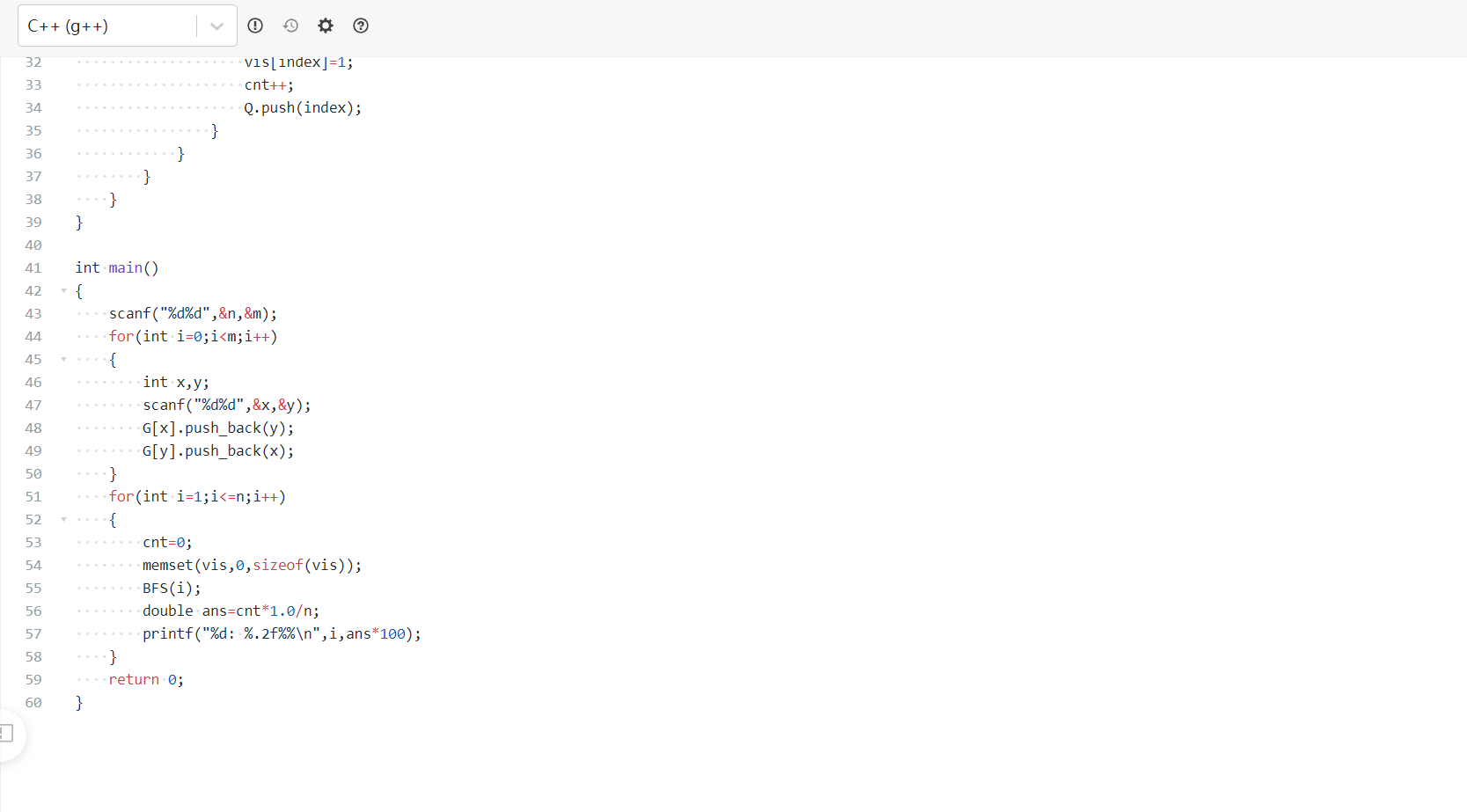
2.2 村村通
伪代码:
定义矩阵;
int main()
{
输入边数和顶点数;
Create(n, e);
int num=0;
num = Prim(n, e);
}
void Create(int n, int e)
{
对矩阵初始化;
修改矩阵;
}
int Prim(int n, int e)
{
int closet[];//保存顶点下标
int lowcost[];//保存权值
int cost = 0;
lowcost[1] = 0;
lowcost[1] = 0;
初始化lowcost[]和closet;
for (i = 2; i <= 2; i++)
{
初始化min,j,k;
while (j < n)
{
找到权值最小的点记录下标;
}
if (判断下标是否改变, 若有证明连通)
{
记录cost和访问顶点操作;
}
else return -1;
修改lowcost和closet;
}
}
代码截图:
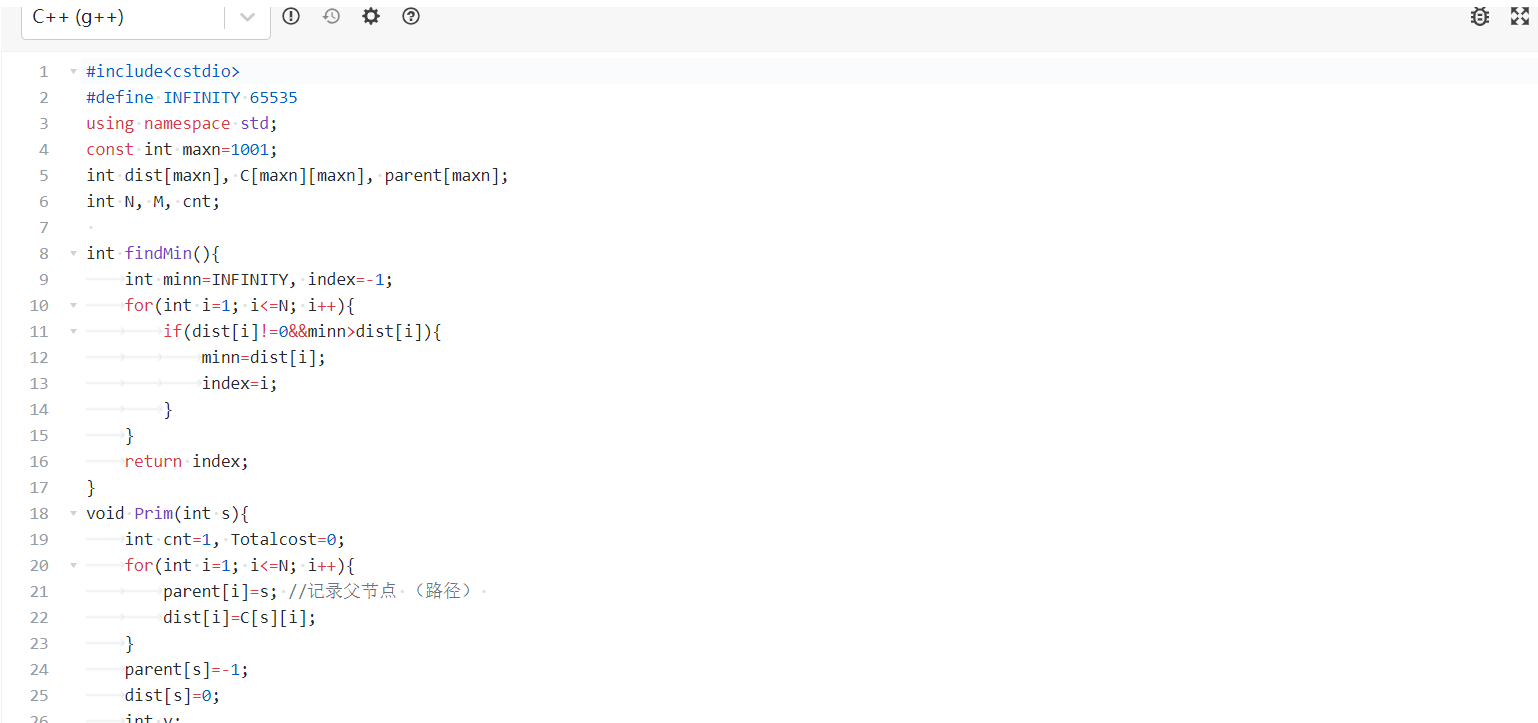





 浙公网安备 33010602011771号
浙公网安备 33010602011771号