AGC011 题解
A - Airport Bus
贪心从前往后加入乘客,显然一班公交的出发时间应当等于某个乘客的抵达时间,枚举到当前乘客时,贪心的发最少的车直到恰好能加入当前乘客。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
int sig = 1; ll num = 0; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
return num * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, c, k, a[N], front;
int main() {
int i, ans = 0; n = Read(), c = Read(), k = Read();
for(i = 1; i <= n; i++) a[i] = Read();
sort(a + 1, a + n + 1), front = 1;
for(i = 1; i <= n; i++) while(front <= i && a[i] > a[front] + k) { int c_ = c, lim = a[front] + k; ans++; while(c_-- && front <= i && a[front] <= lim) front++; }
Write(ans + (n - front + c) / c);
}
B - Colorful Creatures
考虑按大小从小到大排序,一个生物若要活到最后就一定先贪心吃掉比他小的所有生物,而如果能吃到恰好比他大的生物中最小的那个生物,考虑现在他的大小等于那个大的生物吃掉比他小的所有生物的大小,于是成为最后的生物的生物大小一定是一个后缀,所以随便判。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
int sig = 1; ll num = 0; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
return num * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n;
ll a[N], s[N];
int main() {
int i; n = Read();
for(i = 1; i <= n; i++) a[i] = Read();
sort(a + 1, a + n + 1);
for(i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
for(i = n - 1; i; i--) if(s[i] * 2 < a[i + 1]) break;
Write(n - i);
}
C - Squared Graph
直接将二元组视为原图中的两个点 \(a, b\)。
考虑 \(a, b\) 只要一个所在的连通块不是二分图,那么所有满足分别与 \(a, b\) 同属于一个连通块的 \(c, d\),一定有 \((a, b)\) 与 \((c, d)\) 连通,这两个连通块会有 \(1\) 的贡献,否则会有 \(2\) 的贡献。
于是我们处理出原图中有多少个二分图的连通块,特殊处理孤立点的情况,此时对于一个孤立点 \(u\) 和任意一点 \(v\),在新图上 \((u, v),(v, u)\) 定是孤立点。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
int sig = 1; ll num = 0; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
return num * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, m, cnt, r[3];
bool suc, vis[N], col[N];
vector<int> e[N];
void Dfs(int u, bool col_) {
vis[u] = true, col[u] = col_, cnt++;
for(auto v : e[u]) if(!vis[v]) Dfs(v, col_ ^ 1);
else suc &= (col_ != col[v]);
}
int main() {
int i; n = Read(), m = Read();
for(i = 1; i <= m; i++) { int u = Read(), v = Read(); e[u].emplace_back(v), e[v].emplace_back(u); }
for(i = 1; i <= n; i++) if(!vis[i]) { cnt = 0, suc = true, Dfs(i, 0); if(cnt == 1) r[2]++; else r[suc]++; }
Write(2ll * r[2] * (n - r[2]) + 1ll * r[2] * r[2] + 1ll * (r[1] + r[0]) * (r[1] + r[0]) + 1ll * r[1] * r[1]);
}
D - Half Reflector
考虑一个情形:小球夹在两个 A 中间并向右移动。
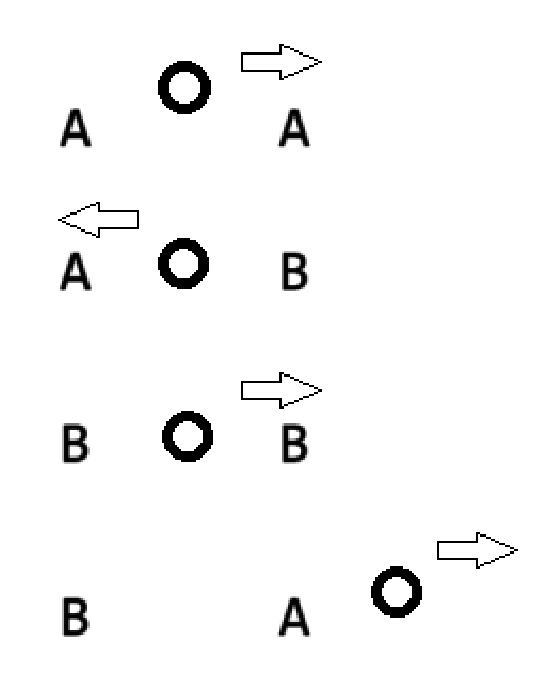
所以考虑一串连续的 A,小球从第 \(1\) 个 A 后向右移动,发现最后除最后一个 A 都被替换为 B。
进一步的,考虑 \(B\) 个 B,和 \(A\) 个 A 的情形,且小球从左端进入,容易发现,小球会从右端出,且原序列变为 \(B - 1\) 个 A,\(A\) 个 B 和 \(1\) 个 A。
因此可以考虑若开头是 A,则变为 B,否则相当于,先将原序列从开头扣去一个,再全局 flip,最后向序列最后添加一个 A。
容易发现 \(n\) 轮删去开头的操作后,序列根据 \(n\) 的奇偶性会变为形如 BABA...BABABA 或 ABABA...BABABA。
对于前一种情况发现序列不再会改变,对于后一种情况,发现一次操作会变为 BBABABA...BABABA 后再变回来,容易根据 \(k\) 的奇偶性判断。
所以我们容易单次 \(O(1)\) 的模拟每一次操作,\(n\) 轮删去开头的操作后直接根据 \(n, k\) 的奇偶性判断序列就可以了。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
int sig = 1; ll num = 0; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
return num * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 200005;
int n, k, a[N << 1];
int main() {
int i, j; bool tag = false; char c; n = Read(), k = Read(), c = getchar();
while(c != 'A' && c != 'B') c = getchar();
for(i = 1; i <= n; i++) a[i] = c - 'A', c = getchar();
for(i = 1; i <= n && k; i++) {
if(!(a[i] ^ tag)) { a[i] ^= 1, i--, k--; continue; }
tag ^= 1, a[i + n] = tag, k--;
}
if(!k) { for(j = i; j < i + n; j++) putchar((a[j] ^ tag) + 'A'); return 0; }
if(n & 1) { putchar((k & 1) ? 'B' : 'A'); for(i = 2; i <= n; i++) putchar((i % 2 == 0) + 'A'); }
else for(i = 1; i <= n; i++) putchar((i & 1) + 'A');
}
E - Increasing Numbers
考虑一个“递增”的数,总能分解成不超过 \(9\) 个 \(111\dots11\) 相加的形式,反过来,不超过 \(9\) 个形如 \(111\dots11\) 的数相加一定能构成一个递增的数,所以不妨把递增的数分解。
考虑枚举答案 \(k\),因为形如 \(111\dots11\) 的数还可以写作 \(\dfrac{10^t-1}{9}\),所以不妨选定一个长度为 \(p\) 的正整数序列 \(T\)(\(p \le 9k\)),满足:
也即:
\(p\) 的最小值即为 \(9N + 9k\) 的数位和。
那么考虑从小到大枚举 \(k\),每次相当于给整个数加上 \(9\),因为进位后数位之和只会减少,所以数位之和最多增加 \(9\),所以 \(k\) 只需枚举到 \(O(n)\) 级别,当然,也容易构造性地证明这一点。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
int sig = 1; ll num = 0; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
return num * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 500505, inf = 1e9;
int n, cnt = 0, a[N];
int main() {
int i, ans = inf; string s; cin >> s, n = s.size(), reverse(s.begin(), s.end());
for(i = 1; i <= n; i++) a[i] = (s[i - 1] - '0') * 9;
for(i = 1; i <= n; i++) { if(a[i] > 9) a[i + 1] += a[i] / 10, a[i] %= 10; cnt += a[i]; if(a[n + 1] > 0) n++; }
if(!cnt) { printf("1"); return 0; }
for(i = 1; ; i++) {
int x = 1; a[x] += 9, cnt += 9;
while(a[x] > 9) cnt -= 9, a[x] -= 10, a[x + 1]++, x++;
if(cnt <= i * 9) { Write(i); return 0; }
}
}
F - Train Service Planning
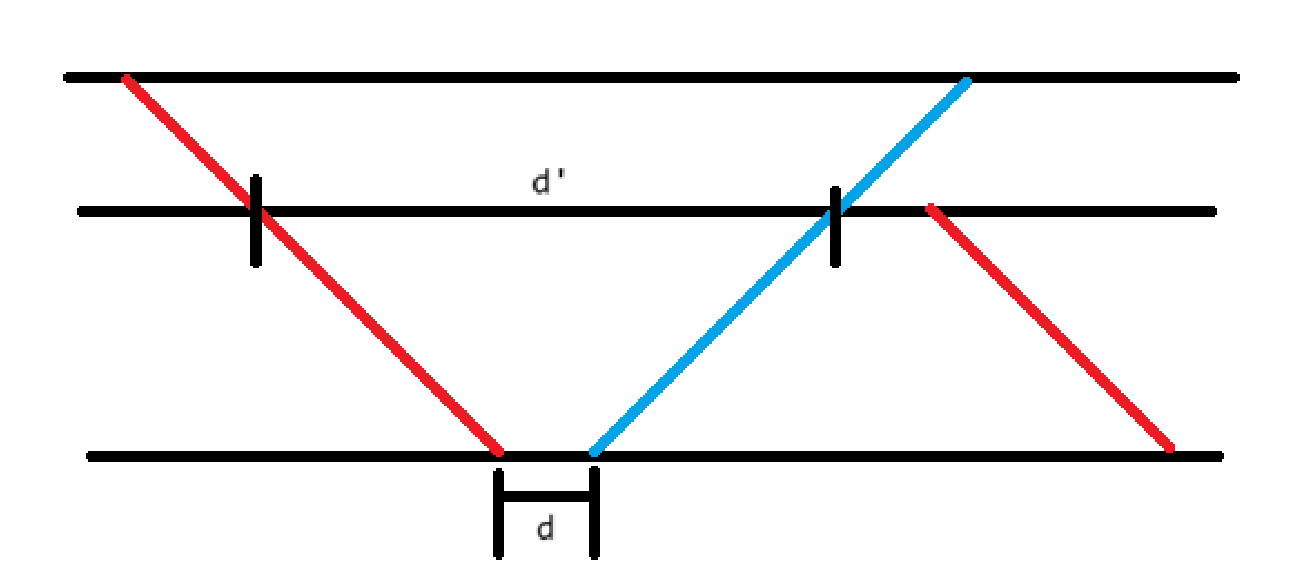
倒过来考虑,下文中横轴为时间,纵轴为站且是倒序的。如图红色表示 \(0 \to N\) 的火车,蓝色表示 \(N \to 0\) 的火车。
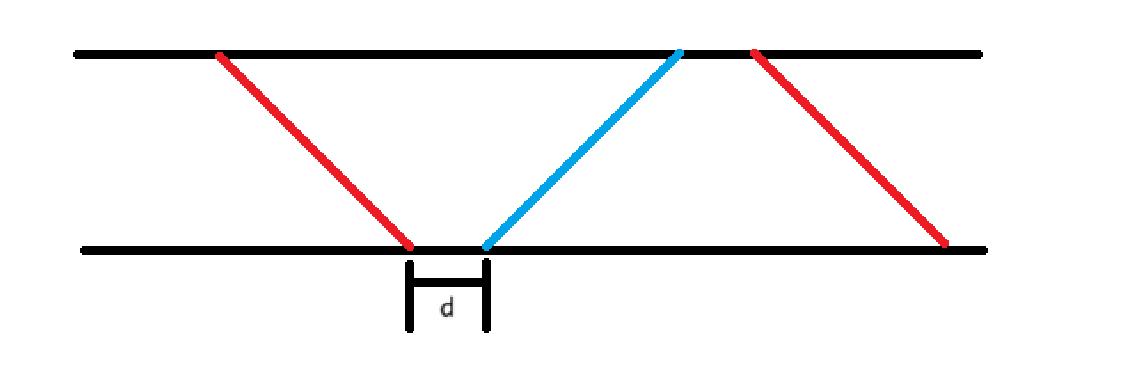
考虑从下往上 DP,发现上一行的决策只和下一行的 \(d\) 有关,所以设 \(f_{i, j}\) 表示考虑完第 \(i\) 行且 \(j = d\) 的情形,并且我们发现,除最后一个区间外,后面的区间可以尽量减小 \(d\),也即:
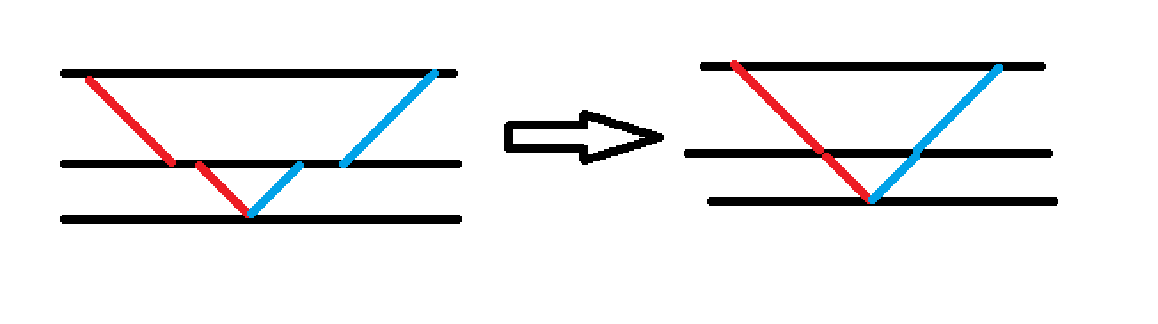
这个时候我们发现对于每一个可能的情况,我们讨论下一个蓝线的位置:
- 与前一条蓝线不相连(即在那一站停靠),发现这个时候红线紧挨蓝线是最优的,即下一个 \(d = 0\),花费是蓝线与下一条红线的上端的距离 \(l\)。
![图片]()
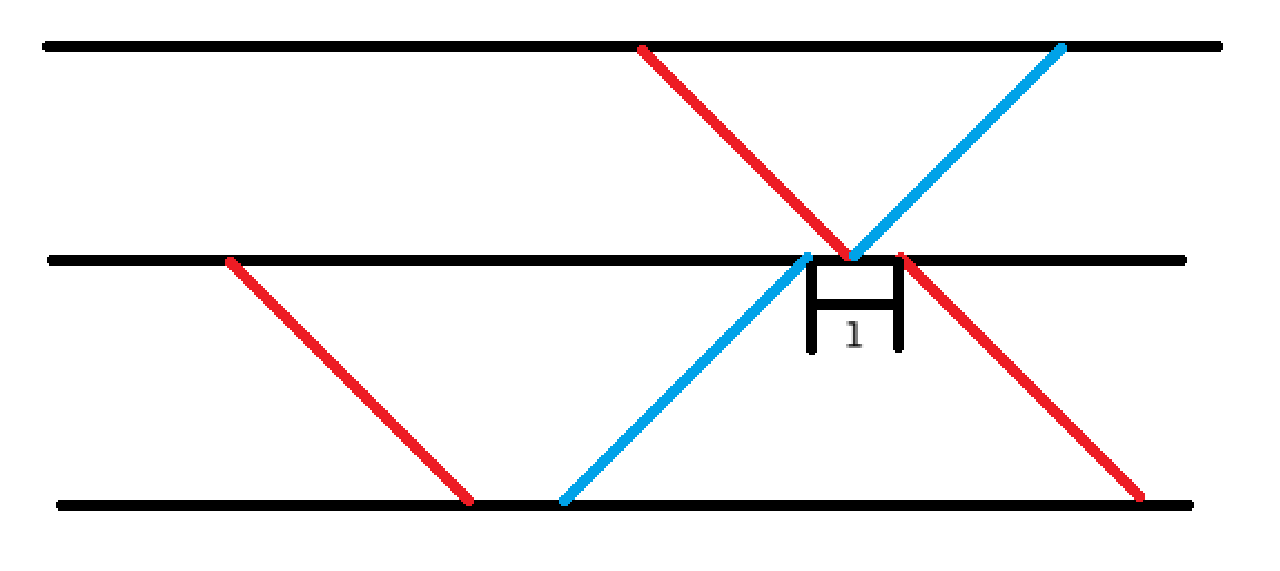
- 与前一条蓝线相连(即在那一站不停靠),发现这个时候本质不同的情况只有这一行的红线也紧挨下一行的红线,则 \(d' = d + 2a_{i + 1}\),花费是 \(0\),但 \(b_i = 0\) 的时候有一个前提条件,即这种情况下上面两条线不能重叠。(\(i\) 表示上面一行)
![图片]()
记 \(a_i\) 的后缀和为 \(s_i\),考虑建立动态开点线段树,考虑完第 \(i\) 行时每个位置 \(x\) 记录当前行 \(j = (x + s_{i + 1}) \bmod k\) 的 \(f_{i, j}\) 值,则对于第一种转移,分析一下式子并拆一下取模,可以转化为两个区间 \(f_{i, j} - x\) 的 \(\min\) 的结果,对于第二种转移可以直接继承,但是要推掉无用状态,也是一个区间(可以循环),直接遍历整个区间暴力修改就可以了,但要判掉区间已经被推过的情况。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
ll x = 0; int sig = 1; char c = getchar();
while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
while(isdigit(c)) x = (x << 3) + (x << 1) + (c ^ '0'), c = getchar();
return x * sig;
}
void Write(ll x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) Write(x / 10);
putchar((x % 10) ^ 48);
}
const int N = 100005;
const ll inf = 1e18;
int n, b[N]; ll a[N], suf[N], k;
struct SegTree {
int cnt, ls[N << 7], rs[N << 7]; bool tag[N << 7]; ll a[N << 7];
void Init() { cnt = 1, a[0] = inf; }
void PushUp(int u) { a[u] = min(a[ls[u]], a[rs[u]]); }
void Tag(int u, int r) { tag[u] = true, a[u] = -r; }
void PushDown(int u, int l, int r) {
if(tag[u]) {
int mid = (l + r) >> 1; if(!ls[u]) ls[u] = ++cnt; if(!rs[u]) rs[u] = ++cnt;
Tag(ls[u], mid), Tag(rs[u], r), tag[u] = false;
}
}
void Modify(int &u, int l, int r, int x, ll y) {
if(!u) u = ++cnt, a[u] = inf;
if(l == r) { a[u] = min(a[u], y - x); return ; }
int mid = (l + r) >> 1; PushDown(u, l, r);
if(x <= mid) Modify(ls[u], l, mid, x, y);
else Modify(rs[u], mid + 1, r, x, y);
PushUp(u);
}
void Clear(int u, int l, int r, int cl, int cr) {
if(!u || a[u] >= inf) return ;
if(cl <= l && r <= cr && (tag[u] || l == r)) { tag[u] = false, a[u] = inf; return ; }
int mid = (l + r) >> 1; PushDown(u, l, r);
if(cl <= mid) Clear(ls[u], l, mid, cl, cr);
if(cr > mid) Clear(rs[u], mid + 1, r, cl, cr);
PushUp(u);
}
void Cover(int &u, int l, int r, int cl, int cr) {
if(!u) u = ++cnt;
if(cl <= l && r <= cr) { Tag(u, r); return ; }
int mid = (l + r) >> 1;
if(cl <= mid) Cover(ls[u], l, mid, cl, cr);
if(cr > mid) Cover(rs[u], mid + 1, r, cl, cr);
PushUp(u);
}
ll Query(int u, int l, int r, int ql, int qr) {
if(!u) return inf;
if(tag[u]) return -min(r, qr);
if(ql <= l && r <= qr) return a[u];
int mid = (l + r) >> 1; ll res = inf; PushDown(u, l, r);
if(ql <= mid) res = min(res, Query(ls[u], l, mid, ql, qr));
if(qr > mid) res = min(res, Query(rs[u], mid + 1, r, ql, qr));
return res;
}
ll Dfs(int u, int l, int r) {
if(!u) return inf;
if(tag[u]) return 0;
if(l == r) return a[u] + l;
int mid = (l + r) >> 1;
return min(Dfs(ls[u], l, mid), Dfs(rs[u], mid + 1, r));
}
}seg;
int main() {
int i, rt = 1; ll ans = 0; n = Read(), k = Read(), seg.Init();
for(i = 1; i <= n; i++) a[i] = Read(), b[i] = Read(), ans += a[i] * 2;
for(i = 1; i <= n; i++) if(b[i] == 1 && a[i] * 2 > k) printf("-1"), exit(0);
while(b[n] == 2) n--;
if(!n) Write(ans), exit(0);
for(i = n; i; i--) suf[i] = (suf[i + 1] + a[i] * 2) % k;
seg.Cover(rt, 0, k - 1, 0, k - 2 * a[n]);
for(i = n - 1; i; i--) {
int l = (k * 3 - 2 * a[i] % k - 2ll * a[i + 1] % k - suf[i + 2] + 1) % k, r = (k * 2 - suf[i + 2] - a[i + 1] * 2 % k) % k, t = r;
ll res = min(seg.Query(rt, 0, k - 1, t, k - 1) + t + k, seg.Query(rt, 0, k - 1, 0, t) + t);
if(b[i] == 1) {
if(l <= r) seg.Clear(rt, 0, k - 1, l, r);
else seg.Clear(rt, 0, k - 1, l, k - 1), seg.Clear(rt, 0, k - 1, 0, r);
}
seg.Modify(rt, 0, k - 1, (k - suf[i + 1]) % k, res);
}
Write(seg.Dfs(1, 0, k - 1) + ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号