AGC007 题解

是的孩子们我又来更 AGC 题解了。

A - Shik and Stone
B - Construct Sequences
C - Pushing Balls
D - Shik and Game
E - Shik and Travel
F - Shik and Copying String

A - Shik and Stone

从 \((1, 1)\) 开始模拟向下走的过程即可。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x >= 10) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 15;
string s[N];
bool vis[N][N];
int main() {
	int n, m, i, j;
	cin >> n >> m;
	string ss(m + 2, '.');
	s[0] = s[n + 1] = ss;
	for(i = 1; i <= n; i++) cin >> s[i], s[i] = "." + s[i] + ".";
	int x = 1, y = 1;
	if(s[x][y] != '#') printf("Impossible"), exit(0);
	while(x != n || y != m) {
		vis[x][y] = true;
		if((s[x + 1][y] == '#') ^ (s[x][y + 1] == '#')) {
			if(s[x + 1][y] == '#') x++;
			else y++;
		}
		else printf("Impossible"), exit(0);
	}
	vis[n][m] = true;
	for(i = 1; i <= n; i++) for(j = 1; j <= m; j++) if(!vis[i][j] && s[i][j] == '#') printf("Impossible"), exit(0);
	printf("Possible");
	return 0;
}

B - Construct Sequences

考虑先令 \(a_{p_i} = i\)，使序列先满足 \(a_{p_i} + b_{p_i} < a_{p_j} + b_{p_j}\)（\(i < j\)），再考虑满足 \(\{a_i\}\) 递增，\(\{b_i\}\) 递减的条件。
想到此时 \(a_i, b_i\) 仍然较小，可以让 \(a_i, b_i\) 分别加上大数 \(c_i, d_i\)，且 \(c_i + d_i\) 总是等于定值 \(T\)，从而让原来序列的值不影响序列单调的性质（由 \(c_i, d_i\) 决定），且原先 \(a_i + b_i\) 的大小关系没有变。
令 \(X\) 为不小于 \(n\) 的一个数，令 \(c_i = X \cdot (i - 1), d_i = X \cdot (n - i)\) 即可，方法很多，但注意不要让序列中出现 \(0\)。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x >= 10) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 20005, T = 20000;
int n, a[N], b[N], rk[N];
int main() {
	int i; n = Read();
	for(i = 1; i <= n; i++) a[Read()] = i;
	for(i = 1; i <= n; i++) a[i] += (i - 1) * T, b[i] += (n - i + 1) * T;
	for(i = 1; i <= n; i++) Write(a[i]), putchar(i == n ? '\n' : ' ');
	for(i = 1; i <= n; i++) Write(b[i]), putchar(i == n ? '\n' : ' ');
	return 0;
}

C - Pushing Balls

考虑 \(d_{2i - 1}\)（\(i\) 是非负整数），令其等于 \(a\)，发现：

若动了前 \(i - 1\) 个球，\(a \gets a + 2x\)，概率为 \(\frac{i - 1}{n}\)；
若动了第 \(i\) 个球，且向左滚，\(a \gets a + 2x\)，概率为 \(\frac{1}{2n}\)；
若动了第 \(i\) 个球，且向右滚，\(a \gets 3a + 3x\)，概率为 \(\frac{1}{2n}\)；
否则，\(a\) 不变，概率为 \(\frac{n - i}{n}\)。
总上，\(a\) 的期望值变为 \(\dfrac{(2i - 1)(a + 2x) + 3a + 3x + (2n - 2i)a}{2n} = a + \dfrac{2a + (4i + 1)x}{2n}\)。

则带入 \(i = 1\)，\(d_1 \gets d_1 + \frac{2d_1 + 5x}{2n}\)。

考虑 \(d_{2i}\)（\(i\) 是非负整数），令其等于 \(b = a + x\)，发现：

若动了前 \(i\) 个球，\(b \gets a + 3x\)，概率为 \(\frac{i}{n}\)；
若动了第 \(i + 1\) 个球，且向左滚，\(b \gets 3a + 6x\)，概率为 \(\frac{1}{n}\)；
否则，\(b\) 不变，概率为 \(\frac{2n - 2i - 1}{n}\)。
总上，\(b\) 的期望值变为 \(\dfrac{2i(a + 3x) + 3a + 6x + (2n - 2i - 1)(a + x)}{2n} = a + x + \dfrac{2a + (4i + 5)x}{2n}\)。

令 \(d_{2i - 1} = a\)，则 \(d_{2i} - d_{2i - 1} = d_{2i + 1} - d_{2i} = x + \frac{2x}{n}\)，所以操作一次后的 \(\{d_i'\}\) 依旧是等差数列，同时，我们还发现 \(d_1' = d_1 + \frac{2d_1 + 5x}{2x}\)，\(x' = x + \frac{2x}{n}\)，同时对于每次操作，球移动距离的期望为 \(d_1 + x \cdot \frac{(1 + 2n - 1) \cdot (2n - 1)}{2 \cdot 2n} = d_1 + \frac{(2n - 1)x}{2}\)，所以递归下去做就可以了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x >= 10) Write(x / 10);
	putchar((x % 10) ^ 48);
}
int main() {
	int n; double d, x, ans = 0; n = Read(), d = Read(), x = Read();
	while(n) ans += d + (2 * n - 1) * x / 2, d += (2 * d + 5 * x) / (2 * n), x += 2 * x / n, n--;
	printf("%.10lf", ans);
	return 0;
}

D - Shik and Game

感性理解过程，一定是一直向右走，走到一个地方就回头（显然在一只熊的地方掉头最优，记这只熊为 \(r\)），走到第一只未领取硬币的熊 \(l\)，再返回，这样每只熊从第一次经过到最后一次经过所需时间为 \(2(a_r - a_l)\)（若不足 \(T\) 秒可以等待），先剔除从 \(0\) 到 \(E\) 处必须消耗的 \(E\) 秒，设 \(f_i\) 表示收集了第 \(1 \sim i\) 只熊的硬币的最小额外时间，容易写出 \(f_i\) 的转移式：

\[f_i = \max_{j < i}\{f_j + \max(2(a_i - a_{j + 1}), T)\} \]

用双指针维护第一个使得区间长度小于 \(T\) 的左端点，就可以分别转移了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 100005;
const ll inf = 1e18;
int n;
ll a, b, x[N], f[N], g[N];
int main() {
	int i, j = 1; n = Read(), a = Read(), b = Read();
	for(i = 1; i <= n; i++) x[i] = Read(), f[i] = inf;
	g[0] = -2ll * x[1];
	for(i = 1; i <= n; i++) {
		while(2 * (x[i] - x[j]) > b) j++;
		if(j > 1) f[i] = g[j - 2] + 2ll * x[i];
		f[i] = min(f[i], f[j - 1] + b), g[i] = min(g[i - 1], f[i] - 2ll * x[i + 1]);
	}
	Write(f[n] + a);
}

E - Shik and Travel

显然这个东西满足二分答案性，那么只要判断是否存在一个方案使得叶子之间的距离小于等于 \(k\)。
考虑 dp，容易发现只要我们进入一颗子树，那么我们一定是把这颗子树走完再跳出这颗子树（考虑该子树根结点与其父亲的连边被经过的次数），所以我们只要记录遍历子树的第一个和最后一个叶子结点到根结点的距离即可。
设 \(f_{u, a, b}\) 表示以 \(u\) 为根的子树，最先遍历的结点到根结点的距离为 \(a\)，最后遍历的结点到根结点的距离为 \(b\)，是否合法。
设 \(l\) 是 \(u\) 的左儿子，\(r\) 是 \(u\) 的右儿子，由上可得起点和终点必然分属不同子树，可得转移（\(w(a, b)\) 表示 \(a, b\) 之间的连边的权值）：

\[f_{u, a, b} = (\bigvee_{c + d + w(l, u) + w(r, u) \le k}\{f_{r, a, c} \land f_{l, d, b}\}) \lor (\bigvee_{c + d + w(l, u) + w(r, u) \le k}\{f_{l, a, c} \land f_{r, d, b}\}) \]

这样的复杂度显然爆炸，考虑优化，发现若 \(f_{u, a, b}\) 显然优于 \(f_{u, a', b'}\)（\(a \le a'\)，\(b \le b'\)），因此我们不必考虑后者，所以对于每个 \(a\)，可以对应一个最小的 \(b\)，而对于每个 \(a' > a\)，都有 \(b' < b\)，对于 \(u\) 我们维护 \(f_{u, a, b} = 1\) 的所有最优数对 \((a, b)\)，用双指针合并两组数对（一共做两遍）就行了。
分析复杂度，上面显然每个数对在一次合并中只可能匹配一个最优数对，所以设要合并的两个数对的集合为 \(S_l, S_r\)，两次合并后数对大小即为 \(S_u = 2 \times \min(|S_l|, |S_r|)\)，单次合并的复杂度为 \(O(|S_l| + |S_r|)\)，很像启发式合并，总复杂度便是 \(O(n \log n)\) 的。
注意要精细实现否则复杂度容易假。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 200005;
int n, fa[N], son[2][N];
ll a[N];
vector<pair<ll, ll> > f[N];
void Merge(vector<pair<ll, ll> > &c, vector<pair<ll, ll> > &a, vector<pair<ll, ll> > &b, ll x, ll u, ll v) {
	if(a.empty() || b.empty()) return ;
	int i = 0, s = b.size(); bool used = false;
	for(auto p : a) {
		while(i < s - 1 && p.second + b[i + 1].first + u + v <= x) i++, used = false;
		if(!used && p.second + b[i].first + u + v <= x) c.emplace_back(p.first + u, b[i].second + v), used = true;
	}
}
void Add(vector<pair<ll, ll> > &f, pair<ll, ll> g) { if(f.empty() || f.back().second > g.second) f.emplace_back(g); }
bool Check(ll x) {
	int i, j, k;
	for(i = n; i; i--) {
		f[i].clear();
		if(!son[0][i]) f[i].emplace_back(0, 0);
		else {
			vector<pair<ll, ll> > g, h;
			Merge(g, f[son[0][i]], f[son[1][i]], x, a[son[0][i]], a[son[1][i]]), Merge(h, f[son[1][i]], f[son[0][i]], x, a[son[1][i]], a[son[0][i]]), j = k = 0;
			int p = g.size(), q = h.size();
			while(j < p && k < q) {
				if(g[j] < h[k]) Add(f[i], g[j++]);
				else Add(f[i], h[k++]);
			}
			while(j < p) Add(f[i], g[j++]);
			while(k < q) Add(f[i], h[k++]);
		}
	}
	return !f[1].empty();
}
int main() {
	int i; n = Read();
	for(i = 2; i <= n; i++) {
		fa[i] = Read(), a[i] = Read();
		if(son[0][fa[i]]) son[1][fa[i]] = i;
		else son[0][fa[i]] = i;
	}
	ll l = 0, r = 2e10, mid, res = r;
	while(l <= r) {
		mid = (l + r) >> 1;
		if(Check(mid)) res = mid, r = mid - 1;
		else l = mid + 1;
	}
	Write(res);
}

F - Shik and Copying String

考虑将过程具象化，发现是类似于以时间为纵轴，以 pos 为横轴画网格图，在网格图上走只能向右、向下的折线。

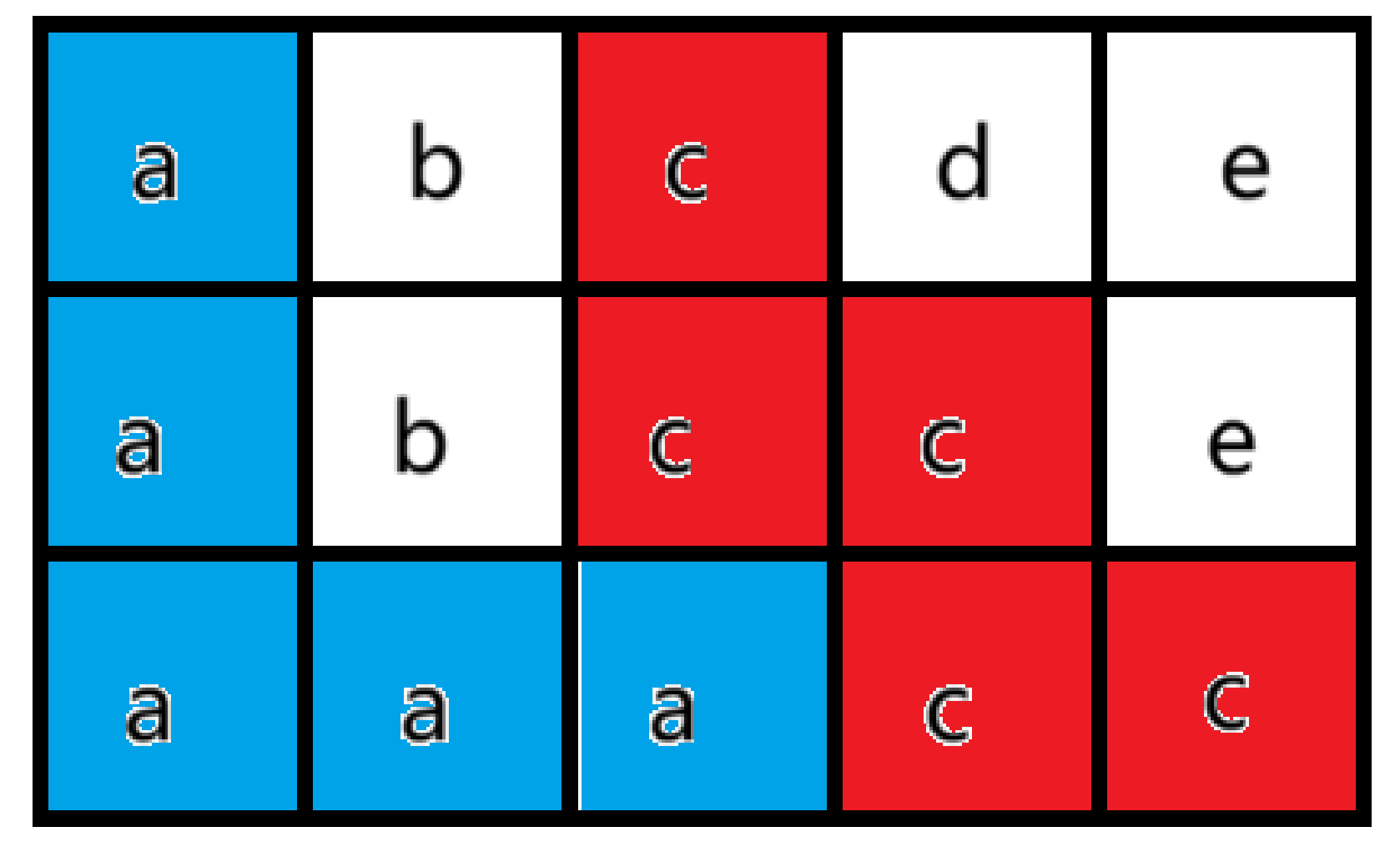
贪心的，我们认为：折线若到达指定位置，应当向下直走，否则向右“靠边”显然不劣。
我们维护向右“拐”的位置（除了最后一行），即图中的 \((2, 3)\) 处。每次向右“拐”的位置都会向左下推进一格，我们用队列从上到下维护它们的纵坐标，如果新加的折线不是正好笔直走下来（这种情况下没有原先遗留的拐点），那么正好前面又新加进一个向右“拐”的点，稍微推导一下就会发现一个向右“拐”的点当前位置为原先的位置减去在它上方的拐点数量。
太困写不下去了，还是看代码好理解一点。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
int n;
string s, t;
int main() {
	int i, j, ans = 0; cin >> n >> s >> t, i = j = n, s = "#" + s, t = "#" + t;
	if(s == t) { printf("0"); return 0; }
	queue<int> q;
	while(i) {
		while(t[i - 1] == t[i]) i--;
		j = min(i, j);
		while(j && s[j] != t[i]) j--;
		if(!j) { printf("-1"); return 0; }
		while(!q.empty() && q.front() - q.size() >= i) q.pop();
		if(j < i) q.emplace(j);
		ans = max(ans, int(q.size() + 1)), i--;
	}
	Write(ans);
}

posted @ 2025-06-19 14:43 Include_Z_F_R_qwq 阅读(7) 评论(0) 收藏举报

刷新页面返回顶部

IncludeZFR