「NOI2007」生成树计数
复盘 \(\color{black}{{\rm P}}\color{red}{{\rm YB}}\) 讲的插头 DP ,写篇题解来祸害社会。
(然而这道题和插头 DP 的关系并不是很大)
Description
给定 \(n\) 和 \(k\) ,一棵有 \(n\) 个点的图,两个点之间存在边当且仅当 \(|u - v| \leq k\) 。
求这个图生成树的数量,答案对 \(65521\) 取模。
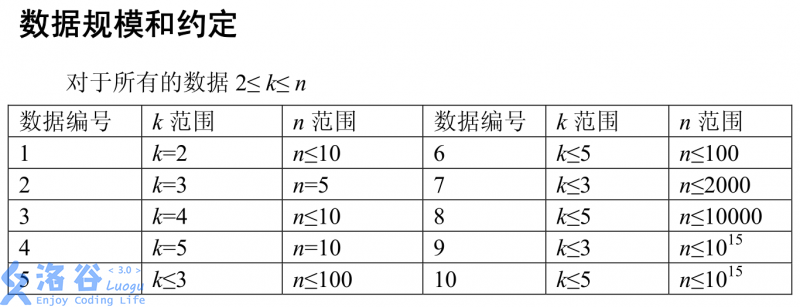
(直接扒图好了(づ ̄3 ̄)づ)
对于 \(100\)% 的数据,有 \(n \leq 10 ^ {15},\ \ 2\leq k \leq 5\) 。
Analysis
看起来题目是直接整上矩阵树定理了的(不会,滚粗了),但是这个数据范围肯定是有其他解法的(我又回来了)。
\(n\) 的范围肯定是要求我们能在 \(O(\log n)\) 时间完成的,而 \(k\) 的范围更是小的离谱。
当然可以考虑 DP ,然后记录目前这点前 \(k\) 个点的状态。因为生成树的要求是联通且无环,所以最好的想法肯定是记录前 \(k\) 个点的联通状态呀,相同连通块的用相同字符表示就行了。
Solution
注意到前 \(k\) 个点前面是不存在完整的 \(k\) 个点供他们连边,所以必定是完全图,然后我们可以在第 \(k\) 个点的地方先硬算一遍答案。
题目非常良心的给出了(不说也应该会的)结论: \(n\) 个结点的完全图的生成树个数为 \(n ^ {n - 2}\) 。
那枚举状态直接硬算就行了。
当然,总状态数就是 \(k ^ k\) 个。
于是就设 \(f(i, S)\) 表示前 \(i\) 个点连完边之后, \([i - k + 1,\ i]\) 这 \(k\) 个点的联通状态为 \(S\) 。
首先,对于下一个点 \(i + 1\) ,我们要知道它要和哪些点连边,这是 \(O(2 ^ k)\) 的。
其次,我们还要判断是否合法:
-
假设有两个点处在同一个连通块但是 \(i + 1\) 却都连边了,那就成环了,不合法!
-
假如离 \(i + 1\) 最远的点 \(i - k + 1\) 没有属于任何一个连通块,那么 \(i + 1\) 不和它连边的话,下一个点 \(i + 2\) 就不能和它连边,这样出现单独的连通块肯定也是不合法的!
又没有什么特殊办法能快速排查,所以又是 \(O(k)\) 的。
所以对于当前点的每个状态 \(S\) ,我们需要 \(O(2 ^ k \cdot k)\) 的时间转移到下一个点的某些状态上。
目前来看,总时间复杂度就是 \(O(nk \cdot (2k) ^ k)\) ,能过 \(60\) 分。
其实可能想到一半就会感觉不对劲,哪里会有 \(k ^ k\) 个状态呢,就比如 \((112)\) 和 \((221)\) 怎么看怎么一样吧。
于是想到了最小表示法,如果两个图联通状态一致,那么最小表示法一定一样,就不会重。然后一试,好家伙,在 \(k = 5\) 的时候也只有 \(52\) 种不同的状态,时间复杂度就变成了 \(O(52nk \cdot 2 ^ k)\) , \(80\) 分拿捏了。
现在瓶颈变成了从一开始就想动但是还没动的 n 上。其实已经想到这里的话也不会有太大的问题,很容易发现转移的时候当前点仅和上一个点有关。并且对于每一个状态,转移是唯一的,所以我们干脆把转移写成矩阵,矩阵快速幂就可以解决。
那时间就变成了 \(O(52k \cdot 2 ^ k + (52) ^ 3 \cdot \log n)\) ,然后你就可以拿到了 \(100\) 分了。
(其实还是和插头 DP 的实现有一定联系的)
Code
Code
/*
*/
#include
//#define int long long
using namespace std;
typedef long long ll;
const int N = 54, M = 3128, mod = 65521;
int k, m, Cnt, p[N], rev[M], ans; ll n;
int f[N], g[N][N], h[N][N], I[N][N];
inline ll read() {
ll s = 0, w = 1;
char ch = getchar();
while (!isdigit(ch)) {if (ch == '-') w = -1; ch = getchar();}
while (isdigit(ch)) {s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
return s * w;
}
inline int mul(int a, int b) {return 1ll * a * b % mod;}
inline int ksm(int a, int b) {
int tmp = 1;
while (b) {
if (b & 1) tmp = mul(tmp, a);
a = mul(a, a); b >>= 1;
}
return tmp;
}
int c[5], vis[5], pl[5], d[5];
inline int mini(int x) {
for (int i = 0; i < k; ++i) c[i] = x % k, x /= k, vis[i] = 0;
int cnt = 0;
for (int i = 0; i < k; ++i) {
if (!vis[c[i]]) vis[c[i]] = 1, pl[c[i]] = cnt++;
c[i] = pl[c[i]];
}
for (int i = k - 1; i >= 0; --i) x = x * k + c[i];
return x;
}
inline void Mul(int a[N][N], int b[N][N]) {
for (int i = 1; i <= m; ++i) for (int j = 1; j <= m; ++j) {
I[i][j] = 0;
for (int k = 1; k <= m; ++k) (I[i][j] += mul(a[i][k], b[k][j])) %= mod;
}
for (int i = 1; i <= m; ++i) for (int j = 1; j <= m; ++j) a[i][j] = I[i][j];
}
inline void ksm(ll b) {
while (b) {
if (b & 1) Mul(h, g);
Mul(g, g); b >>= 1;
}
}
int main() {
k = read(); n = read();
Cnt = ksm(k, k) - 1;
for (int i = 0; i <= Cnt; ++i) {
if (mini(i) == i) p[++m] = i, rev[i] = m;
}
for (int i = 1, x; i <= m; ++i) {
x = p[i];
for (int j = 0; j < k; ++j) c[j] = 0;
for (int j = 0; j < k; ++j) ++c[x % k], x /= k;
x = p[i]; f[i] = 1;
for (int j = 0; j < k; ++j) {
if (c[j] > 1) f[i] *= ksm(c[j], c[j] - 2);
}
}
for (int i = 1, x; i <= m; ++i) {
for (int t = 0; t < (1 << k); ++t) {
x = p[i];
for (int j = 0; j < k; ++j) c[j] = 0, vis[j] = 0;
int fg = 0, blo = -1;
for (int j = 0; j < k; ++j) {
d[j] = x % k; ++c[d[j]]; x /= k;
if ((t >> j) & 1) {
if (vis[d[j]]) {fg = 1; break;}
blo = d[j]; vis[d[j]] = 1;
}
}
if (fg || (c[x % k] == 1 && !(t & 1))) continue;
x = p[i];
if (blo == -1) {
for (int j = 0; j < k; ++j) if (!c[j]) blo = j;
}
else for (int j = 0; j < k; ++j) if (vis[d[j]]) d[j] = blo;
int now = blo;
for (int j = k - 1; j >= 1; --j) now = now * k + d[j];
now = mini(now);
++g[rev[now]][i];
}
}
for (int i = 1; i <= m; ++i) for (int j = 1; j <= m; ++j) g[i][j] %= mod;
for (int i = 1; i <= m; ++i) h[i][i] = 1;
ksm(n - k);
for (int i = 1; i <= m; ++i) (ans += mul(h[1][i], f[i])) %= mod;
printf("%d\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号