AcWing算法提高课【第二章搜索】DFS之联通性模型、DFS之搜索顺序、DFS之剪枝与优化、迭代加深、双向DFS、IDA*
DSF要不要恢复现场,要看题目是什么样子了,看是内部搜索还是外部搜索
如果有所点都在棋盘内部搜索,我们需要保证每个点只能被搜一次,因此就不需要恢复现场。
如果把棋盘当作一个整体的状态,看棋盘不同状态的变化,就需要恢复现场了。
DFS之联通性模型:【内部搜索】
题目:
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,
前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,
问在不走出迷宫的情况下能不能办到。 如果起点或者终点有一个不能通行(为#),则看成无法办到。 注意:A、B不一定是两个不同的点。 输入格式 第1行是测试数据的组数 k,后面跟着 k 组输入。 每组测试数据的第1行是一个正整数 n,表示迷宫的规模是 n∗n 的。 接下来是一个 n∗n 的矩阵,矩阵中的元素为.或者#。 再接下来一行是 4 个整数 ha,la,hb,lb,描述 A 处在第 ha 行, 第 la 列,B 处在第 hb 行, 第 lb 列。 注意到 ha,la,hb,lb 全部是从 0 开始计数的。 输出格式 k行,每行输出对应一个输入。 能办到则输出“YES”,否则输出“NO”。 数据范围 1≤n≤100 输入样例: 2 3 .## ..# #.. 0 0 2 2 5 ..... ###.# ..#.. ###.. ...#. 0 0 4 0 输出样例: YES NO
分析:
简单的DFS搜索路径问题,DFS只可以说明是否存在路径,但是不能说明最短路。 在写DFS的时候,还是要想象它的递归搜索树的样子,这更形象,更具体。
代码:
#include <cstdio>
using namespace std;
const int N = 110;
int n;
char g[N][N];
int sx, sy, ex, ey;
bool st[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
bool dfs(int sx, int sy)
{
if (g[sx][sy] == '#') return false;
if (sx == ex && sy == ey) return true;
st[sx][sy] = true;
for (int i = 0; i < 4; i ++ )
{
int x = sx + dx[i], y = sy + dy[i];
if (x < 0 || x >= n || y < 0 || y >= n) continue;//我就有个疑惑了,这里return false 和continue有什么区别
// if (x < 0 || x >= n || y < 0 || y >= n) return false;//这里,如果return false,直接返回给了调用它的函数,而不会是一个状态的末尾
if (st[x][y]) continue;
// printf("sx: %d, sy: %d || x: %d, y: %d\n", sx, sy, x, y);
if (dfs(x, y)) return true;
}
return false;
}
void work()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);
scanf("%d%d%d%d", &sx, &sy, &ex, &ey);
// for (int i = 0; i < n; i ++ ) printf("%s\n", g[i]);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= n; j ++ )
st[i][j] = false;
if (dfs(sx, sy)) puts("YES");
else puts("NO");
return;
}
int main()
{
int T; scanf("%d", &T);
while (T -- )
{
work();
}
return 0;
}
题目:
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。 你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。 请写一个程序,计算你总共能够到达多少块黑色的瓷砖。 输入格式 输入包括多个数据集合。 每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。 在接下来的 H 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下 1)‘.’:黑色的瓷砖; 2)‘#’:红色的瓷砖; 3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。 当在一行中读入的是两个零时,表示输入结束。 输出格式 对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。 数据范围 1≤W,H≤20 输入样例: 6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0 输出样例: 45
分析:
这里面的,有返回值的DFS还是理解的不到位的,还要再看看的。
代码:
#include <cstdio>
using namespace std;
const int N = 30;
int m, n;
char g[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
bool st[N][N];
int dfs(int sx, int sy)
{
int ans = 1;
st[sx][sy] = true;
for (int i = 0; i < 4; i ++ )
{
int x = sx + dx[i], y = sy + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (st[x][y]) continue;
if (g[x][y] == '#') continue;
// printf("before:x= %d || y= %d || ans= %d\n", x, y, ans);
ans += dfs(x, y);
// printf("after:x: %d || y= %d || ans= %d\n", x, y, ans);
}
// printf("last: x= %d || y = %d\n", x, y);
// printf("last: ans= %d\n", ans);
return ans;
}
void work()
{
for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
st[i][j] = false;
// for (int i = 0; i < n; i ++ ) printf("%s\n", g[i]);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (g[i][j] == '@')
{
printf("%d\n", dfs(i, j));
return;
}
}
int main()
{
while (~scanf("%d%d", &m, &n))
{
if (!n && !m) break;
work();
}
return 0;
}
【从这开始就是外部搜索了】
外部搜索:采取一个搜索顺序,使得我们可以将所有方案全部枚举到。
恢复现场:我下去的时候什么样子,回来的时候要还是什么样子
DFS之搜索顺序:
题目:
马在中国象棋以日字形规则移动。 请编写一段程序,给定 n∗m 大小的棋盘,以及马的初始位置 (x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。 输入格式 第一行为整数 T,表示测试数据组数。 每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标 n,m,x,y。 输出格式 每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,若无法遍历棋盘上的所有点则输出 0。 数据范围 1≤T≤9, 1≤m,n≤9, 0≤x≤n−1, 0≤y≤m−1 输入样例: 1 5 4 0 0 输出样例: 32
分析:
这一题,让我们计算棋盘有多少种方案数,无疑了,一定需要恢复现场。 当我们到了当前层的时候,将当前层状态标记,然后dfs下面一层,然后紧跟着就要将状态恢复现状。 注意,我们记方案数的时候,就是看叶子节点能否到达我们预设状态,也就是可不可以走完整个棋盘,也就是可不可以拓展n*m个点,如果可以就给他记个方案数。
代码:
#include <cstdio>
using namespace std;
const int N = 20;
int n, m, x, y;
bool st[N][N];
int ans;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {-1, -2, -2, -1, 1, 2, 2, 1};
void dfs(int sx, int sy, int u)
{
if (u == n * m )
{
ans ++;
return;
}
//当前节点向下搜素,将当前节点制成true
st[sx][sy] = true;
for (int i = 0; i < 8; i ++ )
{
int x = dx[i] + sx, y = dy[i] + sy;
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (st[x][y]) continue;
dfs(x, y, u + 1);
}
st[sx][sy] = false;
}
void work()
{
scanf("%d%d%d%d", &n, &m, &x, &y);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
st[i][j] = false;
ans = 0;
dfs(x, y, 1);
printf("%d\n", ans);
return;
}
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
work();
}
return 0;
}
题目:
单词接龙是一个与我们经常玩的成语接龙相类似的游戏。 现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”,每个单词最多被使用两次。 在两个单词相连时,其重合部分合为一部分,例如 beast 和 astonish ,如果接成一条龙则变为 beastonish。 我们可以任意选择重合部分的长度,但其长度必须大于等于1,且严格小于两个串的长度,例如 at 和 atide 间不能相连。 输入格式 输入的第一行为一个单独的整数 n 表示单词数,以下 n 行每行有一个单词(只含有大写或小写字母,长度不超过20),输入的最后一行为一个单个字符,表示“龙”开头的字母。 你可以假定以此字母开头的“龙”一定存在。 输出格式 只需输出以此字母开头的最长的“龙”的长度。 数据范围 n≤20 输入样例: 5 at touch cheat choose tact a 输出样例: 23 提示 连成的“龙”为 atoucheatactactouchoose。
分析:
一个字符串可以使用最多2次。 搜的时候,先处理好重叠部分就会很好写了。
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30;
int n;
string s[N];
int pub[N][N];//两个字符串i与j的最短的公共部分为多少,只有公共部分越短,总字符串才能越长
int cnt[N];
int ans;
void dfs(string str, int last)
{
ans = max(ans, (int)str.size());
cnt[last] ++;
for (int i = 0; i < n; i ++ )
if (pub[last][i] && cnt[i] < 2)
dfs(str + s[i].substr(pub[last][i]), i);
cnt[last] --;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> s[i];
char c; cin >> c;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
for (int k = 1; k < (int)min(s[i].size(), s[j].size()); k ++ )
if (s[i].substr(s[i].size() - k, k) == s[j].substr(0, k))
{
pub[i][j] = k;
break;
}
for (int i = 0; i < n; i ++ )
if (s[i][0] == c)
dfs(s[i], i);
cout << ans << "\n";
return 0;
}
题目:
给定 n 个正整数,将它们分组,使得每组中任意两个数互质。 至少要分成多少个组? 输入格式 第一行是一个正整数 n。 第二行是 n 个不大于10000的正整数。 输出格式 一个正整数,即最少需要的组数。 数据范围 1≤n≤10 输入样例: 6 14 20 33 117 143 175 输出样例: 3
分析:
我觉得这题是一道好题,可以很好的那他来练手,练DFS 可以通过多个角度去搜索,可以通过不同的方法去搜索。 可以一组一组的搜,可以一个一个的搜。
可以以每个元素为状态,判断当前元素可以放到那一组中去。
可以以组为状态,判断每个元素剩余元素是否可以放到当前组,(这里的尝试就说明我们需要恢复现场)没有被放入的,如果可以放,就将它尝试放入,、
如果可以放入,那我们就不需要再新开一个数组,如果对于当前数组来说,剩余的所有元素都不能放入当前数组了,那我们才新开一个数组存放。
优先将所有能加的数都加到当前数组,加满为止。
枚举那个数可以放到当前组是一个组合问题,而不是一个排列问题,放入当前数组的元素不需要考虑顺序,所以我们可以搜索状态的时候,可以加一个last
代码:
//先搜第一组,组内没有元素,当前一共搜了0个元素,从0号下标开始搜
//start,对于当前组来说,start前面的元素都被搜索过了,从当前位置开始搜索
#include <cstdio>
using namespace std;
const int N = 11;
int n;
int a[N];
int g[N][N];
int ans = N;
bool st[N];
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
bool check(int cnt, int ct, int i)
{
for (int j = 0; j < ct; j ++ )
if (gcd(g[cnt][j], a[i]) > 1) return false;
return true;
}
void dfs(int u, int cnt, int ct, int last)
{
if (cnt >= ans) return;
if (u == n)
{
ans = cnt;
return;
}
//枚举所有元素,判断是否可以放入最后一组(当前组),前面的元素都被枚举过了,上一个搜索的位置开始搜last
bool flag = true;
for (int i = last; i < n; i ++ )
if (!st[i] && check(cnt, ct, i))
{
st[i] = true;
g[cnt][ct] = a[i];
dfs(u + 1, cnt, ct + 1, i);
st[i] = false;
flag = false;
}
//我们的当前组(最后一组)已经没有元素可以加进去了
if (flag) dfs(u, cnt + 1, 0, 0);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
dfs(0, 1, 0, 0);
printf("%d\n", ans);
return 0;
}
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 11;
int n;
int a[N];
int g[N][N], p[N];
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
bool check(int g[], int t, int ct)
{
for (int i = 0; i < ct; i ++ )
if (gcd(g[i], t) > 1) return false;
return true;
}
int ans = N;
int cnt;
void dfs(int u)
{
if (u == n + 1)
{
ans = min(ans, cnt);
return;
}
//将当前元素尝试加入每一个组
for (int i = 0; i < cnt; i ++ )
if (check(g[i], a[u], p[i]))
{
g[i][p[i] ++ ] = a[u];
dfs(u + 1);
g[i][-- p[i]];
}
//尝试为这个元素新开一个组
g[cnt ++ ][p[cnt - 1] ++ ] = a[u];
dfs(u + 1);
g[-- cnt][-- p[cnt]];
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
dfs(1);
printf("%d\n", ans);
return 0;
}
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 11;
int n;
ll a[N];
inline ll gcd(ll a, ll b)
{
return b ? gcd(b, a % b) : a;
}
int ans = N, cnt;
ll g[N];
void dfs(int u)
{
if (u == n)
{
ans = min(ans, cnt);
return;
}
for (int i = 0; i < cnt; i ++ )
if (gcd(g[i], a[u]) == 1)
{
g[i] *= a[u];
dfs(u + 1);
g[i] /= a[u];
}
g[cnt ++ ] = a[u];
dfs(u + 1);
g[-- cnt] /= a[u];
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%lld", a + i);
for (int i = 0; i < n; i ++ ) g[i] = 1;
dfs(0);
printf("%d\n", ans);
return 0;
}
DFS之剪枝与优化:
题目:
翰翰和达达饲养了 N 只小猫,这天,小猫们要去爬山。 经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。 翰翰和达达只好花钱让它们坐索道下山。 索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN。 当然,每辆缆车上的小猫的重量之和不能超过 W。 每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山? 输入格式 第 1 行:包含两个用空格隔开的整数,N 和 W。 第 2..N+1 行:每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。 输出格式 输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。 数据范围 1≤N≤18, 1≤Ci≤W≤108 输入样例: 5 1996 1 2 1994 12 29 输出样例: 2
分析:
小猫爬山这题,用DFS来搜索所有状态空间,找到题目所求性质MIN。让车辆的个数最少。 思路:搜索运送的小猫数量作为我们的状态空间。 优化:1.给小猫降序处理,先安放体重较大的。2.如果搜索小车数量大于等于当前答案,及时剪枝,因为这个搜索分支最好的情况也不比ans优。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 20;
int n, m;
int a[N];
int ans = N;
int s[N], cnt;
void dfs(int u)
{
//如果此时的cnt已经大于等于我们的ans了,一定不会比现在的情况更优,可以及时剪枝
if (cnt >= ans) return;
if (u == n)
{
ans = cnt;
for (int i = 0; i < cnt; i ++ )
{
// printf("%d\n", s[i]);
}
return;
}
for (int i = 0; i < cnt; i ++ )
if (s[i] + a[u] <= m)
{
s[i] += a[u];
dfs(u + 1);
s[i] -= a[u];
}
s[cnt ++ ] = a[u];
dfs(u + 1);
s[-- cnt] = 0;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
reverse(a, a + n);
dfs(0);
printf("%d\n", ans);
return 0;
}
题目:
数独是一种传统益智游戏,你需要把一个 9×9 的数独补充完整,使得图中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。 请编写一个程序填写数独。 输入格式 输入包含多组测试用例。 每个测试用例占一行,包含 81 个字符,代表数独的 81 个格内数据(顺序总体由上到下,同行由左到右)。 每个字符都是一个数字(1−9)或一个 .(表示尚未填充)。 您可以假设输入中的每个谜题都只有一个解决方案。 文件结尾处为包含单词 end 的单行,表示输入结束。 输出格式 每个测试用例,输出一行数据,代表填充完全后的数独。 输入样例: 4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4...... ......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3. end 输出样例: 417369825632158947958724316825437169791586432346912758289643571573291684164875293 416837529982465371735129468571298643293746185864351297647913852359682714128574936
分析:
这题,难搞,该多敲
代码:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 9, M = 1 << N;
int ones[M], map[M];
int row[N], col[N], cell[3][3];
char str[100];
void init()
{
for (int i = 0; i < N; i ++ )
row[i] = col[i] = (1 << N) - 1;
for (int i = 0; i < 3; i ++ )
for (int j = 0; j < 3; j ++ )
cell[i][j] = (1 << N) - 1;
}
void draw(int x, int y, int t, bool is_set)
{
if (is_set) str[x * N + y] = '1' + t;
else str[x * N + y] = '.';
int v = 1 << t;
if (!is_set) v = -v;
row[x] -= v;
col[y] -= v;
cell[x / 3][y / 3] -= v;
}
int lowbit(int x)
{
return x & -x;
}
int get(int x, int y)
{
return row[x] & col[y] & cell[x / 3][y / 3];
}
bool dfs(int cnt)
{
if (!cnt) return true;
int minv = 10;
int x, y;
for (int i = 0; i < N; i ++ )
for (int j = 0; j < N; j ++ )
if (str[i * N + j] == '.')
{
int state = get(i, j);
if (ones[state] < minv)
{
minv = ones[state];
x = i, y = j;
}
}
int state = get(x, y);
for (int i = state; i; i -= lowbit(i))
{
int t = map[lowbit(i)];
draw(x, y, t, true);
if (dfs(cnt - 1)) return true;
draw(x, y, t, false);
}
return false;
}
int main()
{
for (int i = 0; i < N; i ++ ) map[1 << i] = i;
for (int i = 0; i < 1 << N; i ++ )
for (int j = 0; j < N; j ++ )
ones[i] += i >> j & 1;
while (cin >> str, str[0] != 'e')
{
init();
int cnt = 0;
for (int i = 0, k = 0; i < N; i ++ )
for (int j = 0; j < N; j ++, k ++ )
if (str[k] != '.')
{
int t = str[k] - '1';
draw(i, j, t, true);
}
else cnt ++ ;
dfs(cnt);
puts(str);
}
return 0;
}
题目:
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。 然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。 请你设计一个程序,帮助乔治计算木棒的可能最小长度。 每一节木棍的长度都用大于零的整数表示。 输入格式 输入包含多组数据,每组数据包括两行。 第一行是一个不超过 64 的整数,表示砍断之后共有多少节木棍。 第二行是截断以后,所得到的各节木棍的长度。 在最后一组数据之后,是一个零。 输出格式 为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。 数据范围 数据保证每一节木棍的长度均不大于 50。 输入样例: 9 5 2 1 5 2 1 5 2 1 4 1 2 3 4 0 输出样例: 6 5
分析:
代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 70;
int n;
int a[N];
int sum, len;
bool st[N];
bool dfs(int u, int lens, int start){
// cout << sum << " " << len << " " << u << endl;
if (u * len == sum) return true;
if (lens == len) return dfs(u + 1, 0, 0);
int fail = 0;
for (int i = start; i < n; i ++ )
if (!st[i] && a[i] + lens <= len && fail != a[i])
{
st[i] = true;
if (dfs(u, lens + a[i], i + 1)) return true;
st[i] = false;
fail = a[i];
if (lens == 0 || lens + a[i] == len) return false;
}
return false;
}
int main()
{
while (cin >> n, n)
{
sum = 0;
for (int i = 0; i < n; i ++ )
{
st[i] = 0;
scanf("%d", a + i);
sum += a[i];
}
sort(a, a + n);
reverse(a, a + n);
for (len = a[n - 1]; len <= sum; len ++ )
if (sum % len == 0)
{
if (dfs(0, 0, 0))
{
printf("%d\n", len);
break;
}
}
}
return 0;
}
题目:
7 月 17 日是 Mr.W 的生日,ACM-THU 为此要制作一个体积为 Nπ 的 M 层生日蛋糕,每层都是一个圆柱体。 设从下往上数第 i 层蛋糕是半径为 Ri,高度为 Hi 的圆柱。 当 i<M 时,要求 Ri>Ri+1 且 Hi>Hi+1。 由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 Q 最小。 令 Q=Sπ ,请编程对给出的 N 和 M,找出蛋糕的制作方案(适当的 Ri 和 Hi 的值),使 S 最小。 除 Q 外,以上所有数据皆为正整数。 输入格式 输入包含两行,第一行为整数 N,表示待制作的蛋糕的体积为 Nπ。 第二行为整数 M,表示蛋糕的层数为 M。 输出格式 输出仅一行,是一个正整数 S(若无解则 S=0)。 数据范围 1≤N≤10000, 1≤M≤20 输入样例: 100 2 输出样例: 68
代码:
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, inf = 1 << 30;
int n, m;
int minv[N], mins[N];
int r[N], h[N];
int ans = inf;
void dfs(int u, int s, int v)
{
// cout << v << " " << s << endl;
if (v + minv[u] > n) return;
if (s + mins[u] > ans) return;
if (s + 2 * (n - v) / r[u + 1] >= ans) return;
if (u < 0) return;
if (u == 0)
{
if (v == n) ans = s;
return;
}
for (int i = min((int)sqrt(n - v), r[u + 1] - 1); i >= u; i -- )
for (int j = min((n - v) / i / i, h[u + 1] - 1); j >= u; j -- )
{
int t = 0;
if (u == m) t = i * i;
r[u] = i, h[u] = j;
dfs(u - 1, s + 2 * i * j + t, v + i * i * j);
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) minv[i] = minv[i - 1] + i * i * i;
for (int i = 1; i <= n; i ++ ) mins[i] = mins[i - 1] + 2 * i * i;
r[m + 1] = h[m + 1] = inf;
dfs(m, 0, 0);
if (ans == 1 << 30) cout << 0 << endl;
else cout << ans << endl;
return 0;
}
迭代加深
题目:
满足如下条件的序列 X(序列中元素被标号为 1、2、3…m)被称为“加成序列”: X[1]=1 X[m]=n X[1]<X[2]<…<X[m−1]<X[m] 对于每个 k(2≤k≤m)都存在两个整数 i 和 j (1≤i,j≤k−1,i 和 j 可相等),使得 X[k]=X[i]+X[j]。 你的任务是:给定一个整数 n,找出符合上述条件的长度 m 最小的“加成序列”。 如果有多个满足要求的答案,只需要找出任意一个可行解。 输入格式 输入包含多组测试用例。 每组测试用例占据一行,包含一个整数 n。 当输入为单行的 0 时,表示输入结束。 输出格式 对于每个测试用例,输出一个满足需求的整数序列,数字之间用空格隔开。 每个输出占一行。 数据范围 1≤n≤100 输入样例: 5 7 12 15 77 0 输出样例: 1 2 4 5 1 2 4 6 7 1 2 4 8 12 1 2 4 5 10 15 1 2 4 8 9 17 34 68 77
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110;
int n;
int a[N];
int depth;
bool st[N];
//枚举层数
bool dfs(int u)
{
if (u > depth) return false;
if (u == depth && a[u - 1] == n) return true;
//从当前分支来看,如果已经出现过的和就不要在出现了
memset(st, 0, sizeof st);
for (int i = u - 1; i >= 0; i -- )
for (int j = i; j >= 0; j -- )
{
int t = a[i] + a[j];
if (st[t]) continue;
if (t > n) continue;
if (a[u - 1] * 2 < t) continue;
if (t <= a[u - 1]) continue;
st[t] = true;
a[u] = t;
if (dfs(u + 1)) return true;
}
return false;
}
int main()
{
while (cin >> n, n)
{
a[0] = 1;
for (depth = 1; !dfs(1); depth ++ );
for (int i = 0; i < depth; i ++ ) printf("%d ", a[i]);
puts("");
// printf("%d\n", depth);
}
return 0;
}
双向DFS
题目:
达达帮翰翰给女生送礼物,翰翰一共准备了 N 个礼物,其中第 i 个礼物的重量是 G[i]。 达达的力气很大,他一次可以搬动重量之和不超过 W 的任意多个物品。 达达希望一次搬掉尽量重的一些物品,请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。 输入格式 第一行两个整数,分别代表 W 和 N。 以后 N 行,每行一个正整数表示 G[i]。 输出格式 仅一个整数,表示达达在他的力气范围内一次性能搬动的最大重量。 数据范围 1≤N≤46, 1≤W,G[i]≤231−1 输入样例: 20 5 7 5 4 18 1 输出样例: 19
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 70;
int m, n;
int a[N];
int w[1 << 25], cnt;
int pos;
void dfs(int u, int k, int s)
{
if (u >= k)
{
w[cnt ++ ] = s;
return;
}
dfs(u + 1, k, s);
if ((LL)a[u] + s <= m) dfs(u + 1, k, s + a[u]);
}
int ans;
void dfs(int u, int s)
{
if (u >= n)
{
int l = 0, r = pos - 1;
while (l < r)
{
int mid = l + r + 1>> 1;
if ((LL)w[mid] + s <= m) l = mid;
else r = mid - 1;
}
ans = max(ans, w[r] + s);
return;
}
dfs(u + 1, s);
if ((LL)a[u] + s <= m) dfs(u + 1, s + a[u]);
}
int main()
{
cin >> m >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
sort(a, a + n);
reverse(a, a + n);
dfs(0, n / 2 + 2, 0);
sort(w, w + cnt);
pos = unique(w, w + cnt) - w;
// cout << pos << endl;
// for (int i = 0; i < pos; i ++ ) cout << w[i] << " ";
// cout << endl;
dfs(n / 2 + 2, 0);
// exit(0);
cout << ans << endl;
return 0;
}
IDA*
题目:
给定 n 本书,编号为 1∼n。 在初始状态下,书是任意排列的。 在每一次操作中,可以抽取其中连续的一段,再把这段插入到其他某个位置。 我们的目标状态是把书按照 1∼n 的顺序依次排列。 求最少需要多少次操作。 输入格式 第一行包含整数 T,表示共有 T 组测试数据。 每组数据包含两行,第一行为整数 n,表示书的数量。 第二行为 n 个整数,表示 1∼n 的一种任意排列。 同行数之间用空格隔开。 输出格式 每组数据输出一个最少操作次数。 如果最少操作次数大于或等于 5 次,则输出 5 or more。 每个结果占一行。 数据范围 1≤n≤15 输入样例: 3 6 1 3 4 6 2 5 5 5 4 3 2 1 10 6 8 5 3 4 7 2 9 1 10 输出样例: 2 3 5 or more
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n;
int a[N];
int depth;
int backup[5][N];
int f()
{
int ans = 0;
for (int i = 0; i + 1 < n; i ++ )
if (a[i + 1] != a[i] + 1) ans ++;
return (ans + 2) / 3;
}
bool dfs(int u)
{
if (u + f() > depth) return false;
if (!f()) return true;
for (int l = 0; l < n; l ++ )
for (int r = l; r < n; r ++ )
for (int k = r + 1; k < n; k ++ )
{
for (int i = 0; i < n; i ++ ) backup[u][i] = a[i];
int x, y;
// for (x = r + 1, y = l; x <= k; x ++, y ++ ) a[y] = backup[u][x];
// for (x = l; x <= r; x ++, y ++ ) a[y] = backup[u][x];
for (x = l, y = l + k - r; x <= r; x ++, y ++ ) a[y] = backup[u][x];
for (x = r + 1, y = l; x <= k; x ++, y ++ ) a[y] = backup[u][x];
if (dfs(u + 1)) return true;
for (int i = 0; i < n; i ++ ) a[i] = backup[u][i];
}
return false;
}
void work()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
for (depth = 0; !dfs(0) && depth < 5; depth ++ );
if (depth >= 5) puts("5 or more");
else cout << depth << endl;
return;
}
int main()
{
int T; cin >> T;
while (T -- )
{
work();
}
return 0;
}
题目:
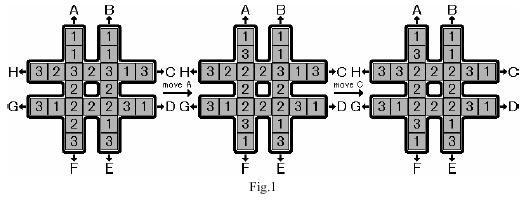
如下图所示,有一个
#形的棋盘,上面有 1,2,31,2,3 三种数字各 88 个。给定 88 种操作,分别为图中的 A∼HA∼H。
这些操作会按照图中字母和箭头所指明的方向,把一条长为 77 的序列循环移动 11 个单位。
例如下图最左边的
#形棋盘执行操作 AA 后,会变为下图中间的#形棋盘,再执行操作 CC 后会变成下图最右边的#形棋盘。给定一个初始状态,请使用最少的操作次数,使
#形棋盘最中间的 88 个格子里的数字相同。
输入格式
输入包含多组测试用例。
每个测试用例占一行,包含 2424 个数字,表示将初始棋盘中的每一个位置的数字,按整体从上到下,同行从左到右的顺序依次列出。
输入样例中的第一个测试用例,对应上图最左边棋盘的初始状态。
当输入只包含一个 00 的行时,表示输入终止。
输出格式
每个测试用例输出占两行。
第一行包含所有移动步骤,每步移动用大写字母 A∼HA∼H 中的一个表示,字母之间没有空格,如果不需要移动则输出
No moves needed。第二行包含一个整数,表示移动完成后,中间 88 个格子里的数字。
如果有多种方案,则输出字典序最小的解决方案。
输入样例:
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 0输出样例:
AC 2 DDHH 2
代码:
#include <cstdio>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
//将八个操作的序号记录下来
int op[8][7] = {
{0, 2, 6, 11, 15, 20, 22},
{1, 3, 8, 12, 17, 21, 23},
{10, 9, 8, 7, 6, 5, 4},
{19, 18, 17, 16, 15, 14, 13},
{23, 21, 17, 12, 8, 3, 1},
{22, 20, 15, 11, 6, 2, 0},
{13, 14, 15, 16, 17, 18, 19},
{4, 5, 6, 7, 8, 9, 10}
};
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
int opposite[8] = {5, 4, 7, 6, 1, 0, 3, 2};
int n;
int a[N];
int path[N];
int depth;
//执行当前操作,移动格子
void work(int u)
{
int tmp = a[op[u][0]];
for (int i = 1; i < 7; i ++ )
a[op[u][i - 1]] = a[op[u][i]];
a[op[u][6]] = tmp;
}
int f()
{
static int cnt[4] = {0};
for (int i = 1; i <= 3; i ++ ) cnt[i] = 0;
for (int i = 0; i < 8; i ++ )
{
// printf("%d ", a[center[i]]);
cnt[a[center[i]]] ++;
}
// printf("\n");
// int ans = max(cnt[1], max(cnt[2], cnt[3]));
int ans = 0, id = 0;
for (int i = 1; i <= 3; i ++ ) if (ans < cnt[i]) ans = cnt[i], id = i;
// printf("id: %d, ans: %d\n", id, ans);
return 8 - ans;
}
bool dfs(int u, int last)
{
// cout << u << " " << last << endl;
// cout << f() << endl;
if (u + f() > depth) return false;
if (!f()) return true;
// cout << u << " " << last << endl;
for (int i = 0; i < 8; i ++ )
{
if (opposite[i] == last) continue;
work(i);
path[u] = i;
if (dfs(u + 1, i)) return true;
work(opposite[i]);
}
return false;
}
int main()
{
string s;
while (getline(cin, s))
{
n = 0;
stringstream ssin(s);
while (ssin >> a[n]) n ++;
if (!a[0]) break;
for (depth = 0; !dfs(0, -1); depth ++ );
// exit(0);
// puts("=-------------------=");
if (!depth) puts("No moves needed"), printf("%d\n", a[6]);
else
{
// for (int i = 0; i < depth; i ++ ) cout << path[i] << " ";
// cout << endl;
for (int i = 0; i < depth; i ++ ) printf("%c", 'A' + path[i]);
printf("\n%d\n", a[6]);
}
// puts("-________________________________-");
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号