CUDA编程模型——组织并行线程3 （2D grid 1D block）

当使用一个包含一维块的二维网格时，每个线程都只关注一个数据元素并且网格的第二个维数等于ny，如下图所示：

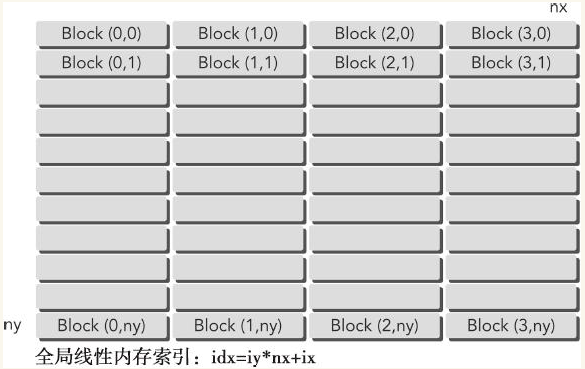
这可以看作是含有二维块的二维网格的特殊情况，其中块儿的第二个维数是1。因此，从块儿和线程索引到矩阵坐标的映射就变成：

ix = threadIdx.x + blockIdx.x * blockDim.x;

iy = blockIdx.y;

从矩阵坐标到全局线性内存偏移量的映射保持不变。核函数如下：

__global__ void sumMatrixOnGPUMix(float *MatA,float *MatB,float *MatC,int nx,int ny)
{
    unsigned int ix=threadIdx.x+blockIdx.x*blockDim.x;
    unsigned int iy=blockIdx.y;
    unsigned int idx=iy*nx+ix;
    if(ix<nx&&iy<ny)
        MatC[idx]=MatA[idx]+MatB[idx];
}

与二维核函数sumMatrixOnGPU2D不同的是，这个新的核函数的唯一优点是每个线程省去了一次整数乘法和整数加法的运算。将块尺寸设置为32，并在此基础上计算网格大小。

dim3 block(32);//x方向上有32个线程块
dim3 grid((nx-1)/block.x+1,ny);

实验运行结果如下图：

将线程块的大小增加到256，实验表现出目前为止最佳的性能：

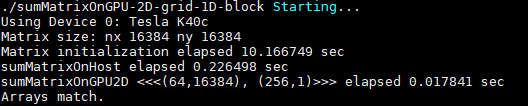
下表是不同核函数实现的结果比较，执行配置都是对应核函数性能较优的参数。

内核函数	执行配置	运行时间
sumMatrixOnGPU2D	(512,1024),(32,16)	0.197 sec
sumMatrixOnGPU1D	(512,1),(32,1)	0.032 sec
sumMatrixOnGPUMix	(64,16384),(256,1)	0.0178 sec

 

 

 

 

 从矩阵加法的例子中看出：

1. 改变执行配置对内核性能有影响；
2. 传统的核函数实现一般不能获得最佳性能；
3. 对于一个给定的核函数，尝试使用不同的网络和线程块大小可以获得更好的性能。

主要参考文献：

1. 《 CUDA C编程权威指南》