DAY 1

T2 :

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+10;
ll s[maxn],js[maxn],inv[maxn];
int cnt[40];
int k,n;

ll ksm(ll a,ll k,ll q)
{
    ll temp=1;
    while(k)
    {
        if(k&1) temp=temp*a%mod;
        a=a*a%mod;
        k>>=1;
    }
    return temp;
}
ll C(ll a,ll b)
{
    if(a<0||b<0||a>b) return 0;
    return js[b]*inv[a]%mod*inv[b-a]%mod;
}
int main()
{
    freopen("card.in","r",stdin);
    freopen("card.out","w",stdout);
    scanf("%d%d",&n,&k);
    js[0]=1;inv[0]=1;
    k--;//因为异或最开始的时候需要有一个初始值，根据初始值的1来分类
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&s[i]);
        js[i]=js[i-1]*i%mod;
        for(int j=0;s[i];j++,s[i]>>=1) cnt[j]+=(s[i]&1);//取出每一位有多少个1
    }
    inv[n]=ksm(js[n],mod-2,mod);//注意这里是计算inv
    //printf("%d \n",js[n]);
    for(int i=n;i>=1;i--) inv[i-1]=inv[i]*i%mod;//
    //for(int i=0;i<31;i++) printf("%d ",inv[i]);
    ll ans=0;
    for(int i=0;i<32;i++)
    {
        ll s1=0,s2=0;
        for(int j=0;j<=k;j+=2) s1=(s1+C(j,cnt[i]-1)*C(k-j,n-cnt[i])%mod)%mod;//如果第一个初始的该位置上面是'1'的话，那么就需要再来偶数个1就可以//此时可以选择的奇数数就少了一个
        for(int j=1;j<=k;j+=2) s2=(s2+C(j,cnt[i])*C(k-j,n-cnt[i]-1)%mod)%mod;//奇数同理
        ans=(ans+(1ll<<i)*(s1*cnt[i]%mod+s2*(n-cnt[i])%mod))%mod;
    }
    printf("%lld",ans*ksm(k+1,mod-2,mod)%mod);//这里在注意一下，因为在k张牌当中，我们选择任意一张作为起始都是可以的，所以说多算了k次，
    return 0;
}

View Code

思路分析：

对于位运算的题目一定是运用位运算和二进制拆分（因为n<32）来进行求解
关于这种有关二进制位的运算
我们照例是对每一位进行考虑
要抓住位运算的本质特征：异或就在于只有奇数个1相互异或才有意义
但同时我们要进行分类讨论，对于第一个选择数的初始值来判断
最后再减去多余情况
一道非常棒的组合数练习题

T4：斜率优化：

本质是在【max或者min的操作下】对dp的递推式子进行一定的改写，在计算每一个状态f(i)时利用单调队列或者单调栈在横坐标单调性和斜率来判断决策j之间的优劣关系，在O（n）的时间内求解线性方程
斜率优化要注意三个地方：
1.如何建立横坐标之间的单调性
2.f(i)的计算式
3.询问斜率的构建式子
4.考虑怎样的同一类j可以转移到i上面
具体步骤：只含

此时我们就知道了对于同一个状态i，两个决策点j1，j2在哪一种状态下能够计算出更优答案f(i)

此时根据决策优劣的判断：

可以证明出，我们需要维护一个下凸包，并且在某个点k1<k k2>2的节点取到最优点
2.2:直接根据式子进行化简：
回到最开始的问题，斜率优化我们需要两个部分，一个是决策的优劣根据斜率的不等式求解，一个是横坐标的单调性保证了下凸包的维护
这一题当中，根据移项我们可以得到

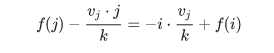
注意这一个式子：三个要素决策点（），询问斜率以及他的单调性，横坐标的单调性：
发现横坐标不具有单调性，这个时候我们需要探究决策的单调性来构造横坐标的单调性
对于两个j1<j2，如果说v1>v2，那么，我们可以由j1->i,肯定不如j1->j2->i来的更优，这就保证了横坐标v一定出现在了坐标轴的最右端
之后维护下凸壳，根据询问斜率递减，那么把比询问斜率大的部分都删掉，就可以保证了
实际上只要让维护的凸包方向相同，两种思考方式的代码是一模一样的。

用单调队列维护凸包点集，操作分三步走：

在本题中步骤

在判断可删图形时有两种方法（以下凸包为例），一种是 slope(Q[t-1],Q[t])<=slope(Q[t],i)，另一种是 slope(Q[t-1],Q[t])<=slope(Q[t-1],i)，都表示出现了可以删去点

该做法时间复杂度为

五.【各种玄学问题】

(ノ°ο°)ノ前方高能预警 (＊°ω°＊)ノ"非战斗人员请撤离!! ＊・_・)ノ

posted @ 2020-11-02 18:44 ILH 阅读(108) 评论(0) 收藏举报

刷新页面返回顶部

DAY 1

五.【各种玄学问题】

公告