图论 基本完成
prime适用于稀疏图,(适用于堆优化)prime
的题目可能会被卡kruskal
适用vector存图的时候适用迭代器用引用的方式来 访问成员(vector的内存是连续的,不是随机引用的关系)
prime算法每次实际上和dij一样的
绝大多数都是用kriskal,稠密图用n^2
prime(或者隐式建图)
隐式建边o(n^2)
1.显示建图
2.
5687 krusal 63分
根据原理,我们贪心排序
留意网格图的性质:我们只需要不构成环就可以了
注意的话,那么值钱加入行或者列的话就有一部分不能加入,计算就可
注意:二分的时候不能应对多组询问
图:有效信息可以转化成树->书上算法
(严格)P4180次小生成树
这条边加入树后出现了一个环,现在需要从环上原来的路径里删去一条边。
删掉路径上的最大边,如果相等的话删去次大边,这样树的权值增加了。
MST(最小生成树)
模型:拆点,拆边,建图:
LCA,树剖,树形dp,计数//我们要关注那些事有效信息,建图就可
BFSPFA
物流运输 P1772 考虑dp dp[i]表示前i天的最小值
有费用的路径问题就可以考虑最短路问题:
(uj,k)分层图变成编号实际上就是 u*k(总共有几层)+k1(k1是第k层)
可以考虑到分阶段的费用问题:
(一定要经过几个阶段,如果中间的状态也有转移可以在单层图里面求解)
逛公园 P3953
注意题目中出现怪异的数据在最短路层面就可以考虑分层图了(或者根据题目的意思自己构造)
这一题的分层就是上升
最短路树:所有在可行最短路上面的边构成的树
连边方式:首先跑一遍最短路,一条边的额外花费时间是w-(d[v]-d[u]),代表这条边是上升几层。
从起点到终点的一条路径(此时不必考虑权值)代表了最终的一条路径,其中每条边的额外花费时间相当于上升的层数。
如果一条边,起点到u的距离+w+v到终点的距离超过了d+K,则这条边不会被经过,可以不加入图。
(首先我们要考虑0权环是否在不在我们可能在合法的最短路上面,所以需要优化先排除这些)
这样子也不会加入路径外的0权,也就是所有0权均会被经过。
可以直接拓扑排序DAG DP计算方案数,而出现环一定是路径上的0权环,输出-1
区间最短路问题:
朴素建图:每一个都连过去
劣化:用一个代表节点,然后代表向实际区间节点连0边
优化建图:对区间的分治划分可以使用线段树或者倍增(类似ST表)
每个结点代表一个区间,连向左右两个子区间。
用对应的方式选择出[l,r]区间代表的一些结点,如果用线段树式则是log个,用倍增式则是2个
然后u到这些点连边
线段树:O(n)个点,O(mlogn)个额外边
倍增:O(nlogn)个点,O(m)个额外边
利用线段树式的区间覆盖的想法来连边(只连恰好能覆盖区间的点)【因为区间是连续的,所以才可以这么做】
ST表 倍增是2^k个点,所以每次只需要选两个点就好,区间之间会有一定的重复
每一个点都需要连向两个边
强连通:有向图中,两个顶点至少存在一条路径
强连通图:每两个顶点都强连通的有向图
强连通分量(Strongly Connected Components):有向图的极大强连通子图
注意:最大不能称为极大:因为极大可以有多个(也就是其中不能再添加)
强联通分量处理DAG上面有依赖的环性问题缩点就可以了
子树的dfs序一定会大于自己
父亲:当前在栈中
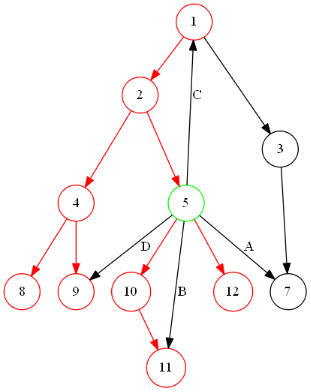
- 红色标记为DFS树 记录dfs序
- A边终点未访问过,为树枝边
- B边终点已被访问过,且dfn[v]>dfn[u],说明在子树中,说明为前向边
- C边终点已被访问过且不在子树中,终点在栈中则为后向边
- D边终点已被访问过且不在子树中且已经出栈,为横叉边 DFS(一定会通过某种方式遍历完所有的边)
- 在一个有向有环图上DFS,找出每一个强连通分量 考虑每一个强连通分量高度最低(离根近)的那个点
- 这些点将DFS树分割成了许多个子树,每个子树中的点组成了一个 强连通分量
- 分割的方法是在dfs同时另外维护一个栈存放节点,离开分割点时把 分割点往下的部分全部取出来就是一个强连通分量。
- 现在需要找到这些分割点(这些所谓的节点就是代表节点)
- stop表示的就是前闭后开
建图:
- 枚举每一条边
- 如果在不同的强联通分量就连边,建立一张新图
- 本质是把强联通分量建成了一张新图()
- 实际上甚至不需要显示建图
- 也就是我们需要一个栈来维护强联通分量下面挂着的分量可消除掉就可以
- 维护一个数组low,low[u]代表点u所能到达子树中的,深度最小的点祖先的dfs序编号
- 初始low[u]=dfn[u]
- 对于边(u,v) 若为树枝边,则用low[v]更新
- 若为后向边,则用dfn[v]更新
- 若为前向边,因为指向的点的信息已经通过树枝边传递过来,所以无需更新
- 若为横叉边,则指向另一个强连通分量,无需更新 当low[u] == dfn[u]时,就是一个分割点
- 它子树中的点都能到达自己(那么自己就是分割点)(如果不能都到达,就是往下面找)
模板:P3387
trajan算法的模板
:
int s[MAXN], stop; int dfn[MAXN], low[MAXN]; int scccnt, sccnum[MAXN]; int dfscnt; inline void tarjan(int now){ dfn[now] = low[now] = ++dfscnt; s[stop++] = now; for (int i = he[now]; i != 0 ; i = ne[i]){ if (!dfn[ed[i]]) { tarjan(ed[i]); low[now] = min(low[now], low[ed[i]]);//数值边 } else if(!sccnum[ed[i]]) {//后向边,前向边同时更新///注意else low[now] = min(low[now], dfn[ed[i]]); } } if (dfn[now] == low[now]) { scccnt++;//统计个数 do { sccnum[s[--stop]] = scccnt; } while(s[stop] != now);//一直出栈 } }
P2746
先考虑DAG:
性质:入度为0的点(topsort,一定可以遍历所有点)出度为0的点
后来我们需要把出度为0和入度为0的两个点
然后呢:如果有强联通分量(在有向边意义下),然后根据强联通分量之间的依赖关系来存图就好
要注意的是:首先要想的是DAG图应该怎么做,或者用强联通分量来转化成DAG
无向图的双连通性
对于无向图,定义双连通性
点双连通:删去任何一个点仍然连通
边双连通:删去任何一条边仍然连通 另一种定义是,任何两点之间至少存在两条不经过相同中间点(边)的路径 如果不满足双连通性
割点(割顶):删去后原图不连通的顶点集合
割边(桥):删去后原图不连通的边集合
满足点(边)双连通性的极大子图称为点(边)双连通分量
一般的题让你求割点或者桥就好了
一张图的点双连通分量之间可能有公共点,边双连通分量之间不可能有公共点
点双连通性不满足传递性,边双连通性满足传递性
点双连通分量一定是边双连通的(无相同点的两条路径一定无相同边)
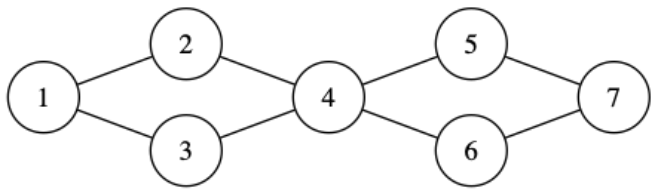
1234 边 4567 边 所以整个1234567都是边联通的
两个点只有一条路径
无向图的dfs树
前向边:指向DFS树中子树中节点的边
横叉边:其他边,即指向DFS树中非子树的边 假如存在这种边(u, v),在v点被dfs访问时,(v, u)一定会被先枚举,则这条边应该是后向边/树枝边。
同样可以维护dfn[]与low[]数组,含义与有向图的dfs相同
无向图的时候就只需要判断就好了
割边(u, v)删去后变为两个连通块,v无法到达u前面的点,即 low[v]>dfn[u]
点u删去后会有至少一个子树中的点无法到达u前面的点,即 存在至少一条树枝边(u, v) low[v]>=dfn[u]
对于根结点需要特别判断,只要有多于一条树枝边则为割点。
求边双联通分量需要判断是否有两个父亲边:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号