背包九讲

 

 

 

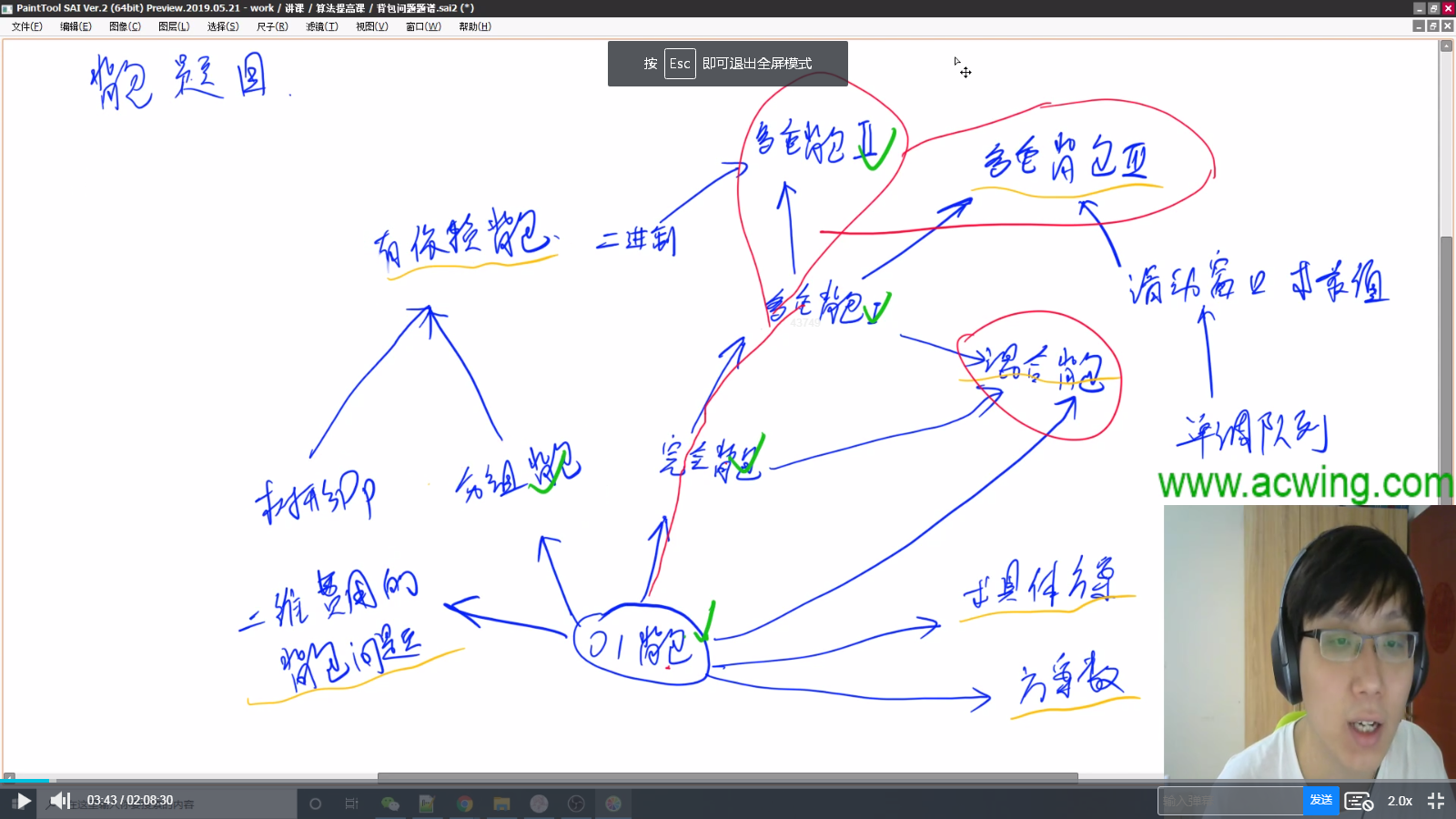
• 背包数：组合类DP

1.01背包

• 集合，属性，最后一步（不重，不漏）
• 分析方法：左边部分（前面i-1的最大价值）和当前选择的物品的价值之和自然是最大的

2.完全背包

• 如果每次要枚举选择几个的话 k=0,1...决策由O(1)变成了O（n）
• 优化方法：考虑枚举求解状态的顺序，考虑决策之间的相近关系
• 

•  

  发现两者之间具有相似的地方：

• 上下两者具有结构相似的地方，直接加上一个w就可以

• 所以说

• f（i,j）=max(f(i-1,j)，f(i，j-v[i]+w[i]）:也可以理解成，从上一维的表格从后向前进行枚举，每次枚举取一个，取两个....

• 【对于状态转移方程的优化方法】：1.针对每一个状态，决策和决策之间的关系；（单调性或者1d1d模型）2.将不变量放在一边，变量放在一边来进行求解3.对于两个相邻的状态，观察相关或者相似的结构和性质 3.枚举不同项式之间的关系

• 当空间优化成1维的时候,只有多重背包从小到大枚举空间，其他都是空间从大到小来枚举

3.多重背包

•  每一个物品有限个：二进制优化
• 

   

   发现：多了一项，这样子黄色方框里面的最大值不能得到整体最大值

• 

   

   也就是发现：我们对于j来说，我们要前面存储的s个dp值的最大值（同时可以排除掉一些奇奇怪怪的）

• 也就是转化成滑动窗口求最大值的问题：（单调队列实现）（其中窗口长度是s）
• 换一种说法，完全背包问题求的是所有前缀的最大值（因为最后一个状态可以转移到前面任意一个的状态）
• 所以说我们要注意，在思考dp问题的时候可以放在新的载体：数轴上面进行思考
• 且注意两个状态之间有偏移量v，所以一定要注意转移过程

4.代码实现：

 

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn=20020;
int f[maxn],g[maxn],q[maxn];
int n,m;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        int v,w,s;scanf("%d%d%d",&v,&w,&s);
        memcpy(g,f,sizeof(f));
        for(int j=0;j<v;j++)//每次列举他们之间所剩下的余数
        {
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=v)
            {
                while(hh<=tt&&q[hh]<k-s*v) hh++;
                if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);//q【】中其实存储的是对应的下标（也就是决策）//实际决策的时候要注意
                while(hh<=tt&&g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w) tt--;//减去偏移量
                q[++tt]=k;
            }
        } 
    }
    printf("%d",f[m]);
    return 0;
}

 

5.二维背包问题：

• 和01背包的一个结合，本质上还是对于状态的枚举和分析
• 注意转移的来源（两种理解方法，【表格法，数轴法】）：从上一行转移过来的，因为我们需要用到左上角的状态，所以左上角的状态不能被更新
• 所以从大到小枚举

•  #include <stdio.h>
   #include <algorithm>
   #include <cstring>
   
   using namespace std;
   
   const int maxn=10010;
   
   int f[maxn][maxn];
   int n,V,M;
   
   int main()
   {
      scanf("%d%d%d",&n,&V,&M);
      for(int i=1;i<=n;i++)
      {
          int v,m,w;
          scanf("%d%d%d",&v,&m,&w);
          for(int j=V;j>=v;j--)
              for(int k=M;k>=m;k--)
              {
                  f[j][k]=max(f[j][k],f[j-v][k-m]+w);
              }
      }
      printf("%d",f[V][M]);
      return 0;
   }

   

5.2潜水员：

• 发现和基本模型有一定的出入的时候
• 我们可以通过改变状态的含义或者改变求解方法来迎合问题
• 这个时候要注意，改变状态的时候就需要改变初始化和状态转移方程
• 换一种说法，那么初始化的时候后（i=0）的时候我们需要让不合法的收益在状态转移的时候是“负收益”,就一定不会从这个状态转移就可以了
• 那么要考虑的东西就多了一项：初始化
• 背包问题扩展：不超过变成了“恰好”

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn=50,maxm=160;
int n,m,k;
int f[maxn][maxm];
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    memset(f,0x3f,sizeof(f));
    f[0][0]=0;
    while(k--)
    {
        int v1,v2,w;
        scanf("%d%d%d",&v1,&v2,&w);
        for(int i=maxn-1;i>=v1;i--)
            for(int j=maxm-1;j>=v2;j--)
            f[i][j]=min(f[i][j],f[i-v1][j-v2]+w);
    }
    int res=1e9;
    for(int i=maxn-1;i>=n;i--)
        for(int j=maxm-1;j>=m;j--)
        res=min(res,f[i][j]);
        printf("%d",res);
        return 0;
}

•  这时候发现：改组数据是可以被hac的
• 理由如下：如果我们考虑去枚举（恰好的话），那么容积需要》=某一个数
• 也就是说，为了满足某一条件，我们可能取到这种方式可能需要的最大值
• 也就是vimax*smax
• 所以说我们如果可以将美剧范围限制在n,m当中，就是更好的结果
• 对于越界的情况是需要思考一下的：
  如果说越界的话：我们要考虑初始化的时候是否合法，只要数组不越界，违反题目规则但是f[i][j]本身表示不合法也是可以的

6.方案数：count

注意一下：朴素版本背包O(

 

 

 优化方式，观察同一状态的上一个决策的关系：f[i,j]=f[i-1,j]+f[i,j-v]

7.对于潜水员的状态计算：我们在划分区间，保证不漏的时候，可以将状态拆分成两部分，然后再将i这一部分的状态抽离，也就是f(i-1这些就可）

至少这个状态唯一的区别在于：（负数和0是一模一样的）

体积最多为x ：初始化为0

体积最少或者恰好是x:初始化为正无穷，f[0][0]=0；

8.动态规划求方案：

• 对应过来的实际上是最短路的问题：
• 也就是我们每次是从哪一个决策转移过来
• 1.不能使用状态压缩2.倒推回来原先是从哪一个状态转移回来（可能同时从两种状态转移）
• 对于字典序最小：大概率是从贪心的角度来选择
• 对于本题角度来说：可选可不选的时候一定要选（字典序最小）
• 那么就转移成：我们从后往前去推到答案（那么还原过来的顺序就是从前往后了）
• 或者可以使用辅助数组记录状态转移

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn=1010;

int f[maxn][maxn];
int v[maxn],w[maxn];
int n,m;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)//二维的状态，体积的顺序没有关系
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    int j=m;//如果有选择就把这一部分的体积减去
    for(int i=1;i<=n;i++)
    {
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i]) printf("%d ",i),j-=v[i];
    }
    return 0;
}

9.分组背包问题：

• 类似于完全背包，不过这时候由于每一个的v,w不同，所以只好将三个状态每一个都枚举一遍
• 注意递推方程，可能都不选所以是f[i][j]要注意
• 然后寻找方案的时候只需要和地推的过程相反就可以了