NOIP 2018 DAY1

 

• 可以说是非常惨了
• 思维上面的局限性暴露的一览无遗：
• 总结的经验也跑得一干二净
• 所以以后怎么做：按照解题表老老实实的进行剖析，珍惜每一次的经验

 

 

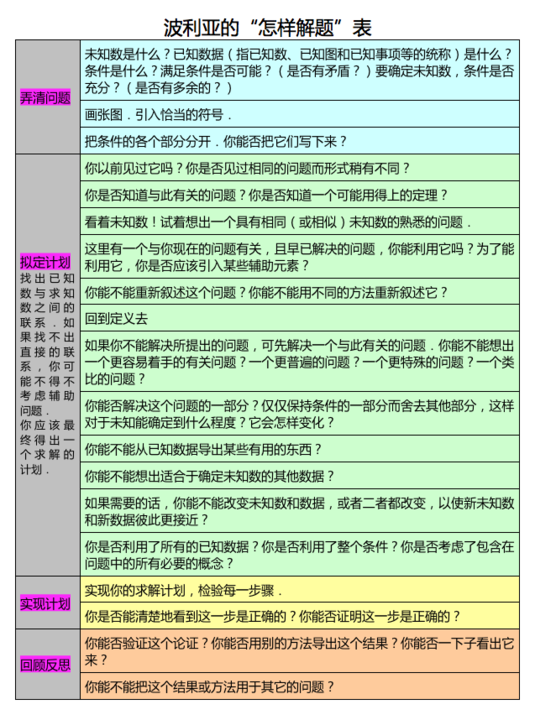
波利亚的怎样解题表

 

• 怎样解题第一步：弄清条件
• 第一：你必需弄清问题       
• 未知是什么？
• 已知是什么？
• 条件是什么？满足条件是否可能？
• 要确定未知，条件是否充分？或者它是否不充分？或者是多余的？或者是矛盾
• 的？
• 画张图，引入适当的符号。
• 把条件的各个部分分开，你能否把它们写下来。
• 怎样解题第二步：拟定计划
• 第二：
• 找出书籍数与未知数之间的联系，如果找不出直接的联系，
• 你可能不得不考虑辅助问题。表中列出了了若干辅助问题，
• 在遇到困境时你可以逐一把这些问题搜索一遍，
• 每个问题的解决都可能是朝向胜利的关键一步！
• 你应该最终得出一个解的计划。 
• 你以前见过它吗？
• 你是否见过相同的问题而形式稍有不同？
• 你是否知道与些有关的问题？
• 你是否知道一个可能用得上的定理？
• 看着未知数，试想出一个具有相同未知数或相似未知数的熟悉的问题？
• 这里有一个与你现在的问题有关，且早已解决的问题，你能不能利用它？
• 你能利用它的结果吗？你能利用它的方法吗？
• 为了利用它，你是否应该引入某些辅助元素？
• 你能不能重新叙述这个问题？你能不能用不同的方法重新叙述它？
• 回到定义去。
• 如果你不能解决所提出的问题，可先解决一个与此有关的问题。
• 你能不能想出一个更容易着手的问题？
• 一个更普遍的问题？
• 一个更特殊的问题？
• 一个类比的问题？
• 你能否解决这个问题的一部分？
• 仅仅保持条件的一部分而舍去其余部分，这样对于未知数能确定到什么程度？它会怎样变化？
• 你能不能从已知数据导出某些有用的东西？

• 你能不能想出适合于确定未知数的其他数据？

• 如果需要的话，

• 你能不能改变未知数或数据，

• 或者二者都改变，以使尊长未知数和新数据彼此更接近？

• 你是否利用了所有的已知数据？

• 你是否利用了整个条件？

• 你是否考虑了包含在问题中的必要的概念？

• 怎样解题第三步：实现计划

• 第三：实行你的计划

• 实现你的求解计划，检验每一步骤
• 你能否清楚地看出这一步骤是正确的？
• 你能否证明这一步骤是正确的？
• 怎样解题第四步：回顾
• 第四：验算所得到的解
• 验算所得到的解。
• 你能否检验这个论证？
• 你能否用别的方法导出这个结果？
• 现在你能不能一下了看出它来？
• 你能不能把这一结果或方法用于其他的问题？
• 若条件或结论做些改变，又将如何解决？

T1

• 接下来，让我们遵照如何解题表的顺序来进行求解：
• 已知每个点的高度，求解最多需要几次填满：
• 关键概念：横向填满：（每一次中间必须全部填满）
• 条件充分，需要处理：
• 画图：模拟数据，发现可以贪心：
• 第二步：
• 考虑两者的联系：（根据高度求解）
• 设置辅助问题：每次贪心的填补最多的层，每一步填补是不是等价的
• 思维1：针对局部放大：发现在填补第i层的时候，如果说i-1层比第i层矮，就一定会被“顺便填上”
• 问题转化为求出来“不能被顺便填上的个数”
• 回顾：
• 1.放大到局部的思想：证明上运用i，j，k至多三个变量
• 2.对于“填补”类的题目就等价于这些“多余的点怎么补上”

T2：

• 已知：原本的序列,求解，新的序列且可以表示以前所有的序列
• 考虑未知和已知的关系：未知的特点：一定只能由已知推导，换一种说法：新的序列只可能从已由序列当中产生
• 关系2：根据样例，若其中若干个数可以表示另一个数，那么哪一个就不需要存在
• 辅助问题：
• 如何标记这些可以表示的数：
• 考虑范围：求解范围一定是1-maxa[i]
• 一个数可能由多个小的数表示，那么只要小的数可以表示，大的数一定可以
• 需要区别可以表示，以及原本存在
• 考虑辅助数组变量：0,1,2
• 求解完毕：
• 回顾：
• 1.求解问题时，需要考虑未知和已知之间的关联和种类，未知的范围，特点，求解顺序等是否需要由已知入手
• 2.不着急下手，考虑清楚再进行
• 3.关于搜索，需要以dp的方式考虑前置状态才能明确搜索方向：（使用多个状态而非bool的辅助数组）
• https://www.luogu.com.cn/blog/CodyTheWolf/Templet（模板）

T3

• 已知：树及其结构，需要的赛道的条数：
• 未知：最大中求解最下(显然是二分）
• 考虑边的特性以及子树的特性
• 辅助问题：二分范围，check函数，
• 1.考虑二分范围：最大一定是树的直径（写法，sum1+sum2）使用dfs解决
• 2.考虑check函数；
• 类比相关的问题：针对每一条边，一共有两种情况：
• 一种是自下而上的一种，一种是由两条边合并而成的（与未知数相关的性质）
• 重解问题：我们转化为了每一个节点和子树在k的条件下能构成多少条边
• 辅助问题：两种情况的处理方式：
• 1.直接一条链就可以：考虑dfs的形式，必然是返回下面（“还没有计算贡献”的最长链），如果加上这个节点的一条边就可以直接统计了；
• 2.否则我们需要保存下来：接下来考虑匹配的问题：
• 显然，根据贪心的思想，我们需要排序的数据结构->multiset
• 每次找到最小的链条【原则：考虑特殊情况：如果只有一条呢？】
• 然后寻找lower——bound【因为更大的需要留着“更有机会产生贡献”】//另一条能够配凑成k的最小值
• 再次细化，考虑细节：
• 如果找到的大小就是自己呢，【如果只有一条这样边，那么久跳过】【两条以上就没有办法】
• 如果已经找到最大仍然不能满足，说明接下来的都不能满足，就一个个匹配过去返回值就好
• 那么剩下的就是最大，把两者进行匹配（因为产生贡献，不能返回上层）
• 最后二分check就可以了
• 回顾：
• 1.树上链的问题一定要根据链的两种情况来进行分类
• 2.根据“自相似原理”，考虑树的问题可以观察每一个节点和子树是怎么产生贡献，可以和bfs进行一个结合
• 3.打暴力的能力应该得到提高和加强：菊花图的分类是由特点的
• 4.对于最小边和最大边的匹配不着急使用双指针
• 5.对于问题的启发性：
• 1.链状图：直接搜索：说明有一部分是直接一条链就产生贡献
• 2.菊花图：分段匹配：大和次大匹配，也就是最小的要和第一个能够使它产生贡献的进行匹配
• 3.m=1树的直径，也就是直接统计树直径的长度就可（这也是二分的上限）
• 由此我们考虑，链状是一条上来的回溯，那么dfs就需要返回子树部分最大，先处理一条，在根据菊花图的启示来分派
• 规律：【树上链状问题，multiset】